目录
Ray Tracing In one Weekend
study notes
图片的输出
PPM Format
P3 # "P3" means this is a RGB color image in ASCII
3 2 # "3 2" is the width and height of the image in pixels
255 # "255" is the maximum value for each color
# The part above is the header
# The part below is the image data: RGB triplets
255 0 0 # red
0 255 0 # green
0 0 255 # blue
255 255 0 # yellow
255 255 255 # white
0 0 0 # black输出图片
./a.out > image.ppmProgress indicator
//outter for
std::cerr << "\rScanlines remaining: " << j << ' ' << std::flush;
//inner for
//...
//outter for end
std::cerr << "\nDone.\n";Vec3 class
- 一般的 3D 程序都需要 4D vector(3D加齐次坐标系)
- vec3 可以用于颜色,位置,方向,offsets 等等
- 使用不同的 alias 来表示不同类型的值
Vec3 的结构
- 变量以成员函数:主要是一个长度为 3 的数组,对该数组的读取,以及一些常规的成员重载,求长度等等。
- 功能函数(友元):加减乘,缩放,点积,叉积,单位向量
颜色的管理函数
主要是将点的上色打包在一起:
void write_color(std::ostream &out, color pixel_color) {
// Write the translated [0,255] value of each color component.
out << static_cast<int>(255.999 * pixel_color.x()) << ' '
<< static_cast<int>(255.999 * pixel_color.y()) << ' '
<< static_cast<int>(255.999 * pixel_color.z()) << '\n';射线&相机&背景
射线
射线由起始点与其在方向上的位移,也就是公式 $P(t) =A + t*b $ 定义:
- $A$ 是起始点
- $b$ 是方向,$t$ 是方向的常数量,有正负,因此 $t*b$ 则能表示在 $b$ 方向的位移
class ray {
public:
ray() {}
ray(const point3& origin, const vec3& direction)
: orig(origin), dir(direction)
{}
point3 origin() const { return orig; }
vec3 direction() const { return dir; }
point3 at(double t) const {
return orig + t*dir;
}
public:
point3 orig;
vec3 dir;
};将射线发射到场景
将射线发射至场景需要三个步骤:
- 假设起始点是我们的眼睛(摄像机位置),那么需要计算眼睛到像素点的射线
- 根据求出的射线判断几何体是否与其相交(如无遮挡,默认画布与射线都相交)
- 以某种规则计算相交点的颜色
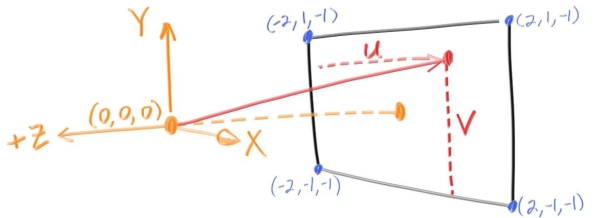
计算射线与相机信息
射线的信息:
- 起始点是我们的眼睛(摄像机点),定义为
(0,0,0) - 终点是画布上的某个位置:
- 该位置通过
u,v坐标与画长宽的乘积表示。u / v 坐标可以视作标准化后的长宽(长宽比坐标) - 再与起始点相减则可得到方向
auto u = double(i) / (image_width-1);
auto v = double(j) / (image_height-1);
ray r(origin, lower_left_corner + u*horizontal + v*vertical - origin);使用线性插值计算颜色
此处颜色的计算是根据当前射线在 $y$ 上的值来作为变量,使用线性插值(Linear interpolation)的方法来计算背景颜色。线性插值(也被成为 lerp)计算颜色的方法是指提供两个基础色,然后提供一个标准化的变量 (处于 $[0,1]$) 来控制颜色。颜色会在这俩个基础色中以线性渐变的形式表现出来。线性插值的公式:
$$\texttt{blendedValue=(1−t)⋅startValue+t⋅endValue}$$
$t$ 值此处与 $y$ 相关。由于我们的画布在 $y$ 上的范围是 $[-1,1]$,因此对 $t$ 也做了标准化处理:
vec3 unit_direction = unit_vector(r.direction());
auto t = 0.5*(unit_direction.y() + 1.0);
(1.0-t)*color(1.0, 1.0, 1.0) + t*color(0.5, 0.7, 1.0);还有一点,场景中的所有点都是基于相机点平移得到的;定义画布上的点(像素的位置)还需要一个 $z$ 方向上的位移,被称为
foal_length。本场景中使用右手定则,因此从相机到画布都需要减掉 focal_length,比如我们扫描的起始点,画布的最左下角:
auto lower_left_corner = origin - horizontal/2 - vertical/2 - vec3(0, 0, focal_length);vec3(0, 0, focal_length)。
添加球体
几何体是否可见的关键在于判断射线是否与其发生了碰撞。
射线-球体相交检测
数学原理以及推导
首先看一下球体的公式:
$$x^2+y^2+z^2 = R^2$$
其中 $(x,y,z)$ 代表在球体上的点。假设该球体的中心为 $(C_x, C_y, C_z)$,则该公式可以写成:
$$(x - C_x)^2 + (y - C_y)^2 + (z - C_z)^2 = r^2$$
假设点 $P$ 的坐标为 $(x, y, z)$,可以发现向量:
$$P-C = (x - C_x), (y - C_y), (z - C_z)$$
而其自身点积的结果正好是上面球体公式扩展后左边的部分:
$$dot((P-C), (P-C)) = (x - C_x)^2 + (y - C_y)^2 + (z - C_z)^2$$
因此,球体的公式可以写成两个向量的点积形式:
$$dot((P-C), (P-C)) = r^2$$
那么,现在我们需要判断射线是否与球相交,只需要知道射线的点是否会落在球体的表面上即可。当射线落在球体表面时,射线的位置应该与球体的位置是相同的;也就是说,我们可以将 $p(t)$ 带入到球体公式里:
$$dot((p(t)-C), (p(t)-C)) = r^2$$
也就是:
$$dot((A + tb -C), (A + tb -C)) = r^2$$
现在利用点积的结合律对该等式进行扩展,我们可以得到一个关于 $t$ 的一元二次方程:
\[
\begin{align*}
&dot((A + tb -C), (A + tb -C)) = r^2 \newline
\Longrightarrow &dot(tb + {\color{Red}(A-C) }), (tb + {\color{Red}(A-C) }) = r^2 \newline
\Longrightarrow &t^2 \cdot \underbrace{{\color{Peach}}dot (b,b)}_\text{a} +t \cdot \underbrace{2 \cdot {\color{Peach} } (b,(A-C))}_\text{b} +\
\underbrace{{\color{Peach} \cdot}((A-C),(A-C))-r^2}_\text{c} = 0
\end{align*}
\]
具体实现
可见的是,射线与球体是否相交的问题,就可以转变为关于 $t$ 的方程是否存在根的问题。这种情况下使用判别式 $b^2 -4ac$ 判断即可。
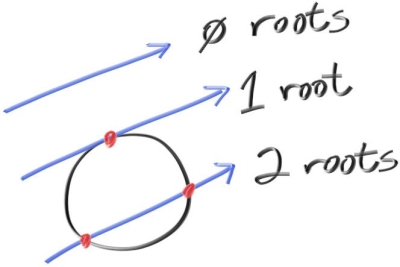
bool hit_sphere(const point3& center, double radius, const ray& r) {
vec3 oc = r.origin() - center; // (A-C)
auto a = dot(r.direction(), r.direction()); //Coefficient of t^2, a
auto b = 2.0 * dot(oc, r.direction()); // Coefficient of t, b
auto c = dot(oc, oc) - radius*radius; // Coefficient, c
auto discriminant = b*b - 4*a*c; // discriminant
return (discriminant > 0);
}法线与多个物体
使用法线信息着色
在圆中,外向法线被定义为从圆心到表现交叉点的向量,也就是交叉点减去圆心: $$ outward\, normal = P-Center; $$
对法线的标准化处理
我们在对法线的可视化过程中有两个地方适用向量的标准化处理:
- 法线本身的标准化处理,有助于 shading
vec3 N = unit_vector(r.at(t) - vec3(0,0,-1));- 法线的可视化技巧:通常对法线的可视化是将法线的
x,y,z与颜色的r,g,b对应起来,因此需要将将法线的范围从 $[-1,1]$ 映射到 $[0,1]$
return 0.5*color(N.x()+1, N.y()+1, N.z()+1);N 处于 $[-1,1]$ 区间,加 1 以后变为 $[0,2]$,在乘以 0.5 后,区间就变为 $[0,1]$ 了。hit_sphere 的返回值
需要注意的是,由于法线的可视化是利用法线本身的数据,因此我们的 hit_sphere 函数不再返回是否碰撞的信息 bool,而是直接返回 t 的值。根据 t 的值:
- 可以通过射线类
Ray成员at找出交叉点 - 计算出该点法线,并交由
ray_color()进行上色
if (discriminant < 0) {
return -1.0;
} else {
return (-b - sqrt(discriminant) ) / (2.0*a);
}t 的返回值使用的是判别式根中为负的计算结果。这个结果将返回离摄像机最近的交叉点:
To correctly find the closest intersection in the interval [t 0 , t 1 ], there are three cases: if the smaller of the two solutions is in the interval, it is the first hit; otherwise, if the larger solution is in the interval, it is the first hit; otherwise, there is no hit.
除此之外, 如果 t 为负,则射线的方向与圆所在的方向相反,因此不可能有交集。这种情况下我们不会进行法线的计算:
if (t > 0.0) {
vec3 N = unit_vector(r.at(t) - vec3(0,0,-1));
return 0.5*color(N.x()+1, N.y()+1, N.z()+1);
}简化圆的射线交叉代码
简化判别式中的 b
令 $b = 2h$,则判别式可以简化为: $$ -b \pm \frac{\sqrt{(b^2-4ac)}}{2a} = -h \pm \frac{\sqrt{(h^2-ac)}}{a} $$
为可被碰撞物体提供抽象类
可以预见的是,渲染中的可碰撞物体并不只有圆,也并不是只有一个。因此,将碰撞这个行为抽象出来是很有必要的。我们将其设计为 hittable 抽象类,该抽象类将允许子类自定义射线碰撞检测的机制。这种机制通常分为两方面:
- 对多个可碰撞物体的的处理机制
- 对特定几何体的射线交叉检测机制
除此之外,我们还会为射线的变量 t 提供一个区间,来控制射线的长度。这样做可以筛选掉一些不必要的结果:比如在对法线对应的交叉点的检测中,我们只需要离我们最近的点(书上提到过,当 $t<0$ 时,只要改变圆心的 $z$ 坐标,依然可以渲染出结果;此时代表我们在看身后的物体),此时通过 t 的范围就可以将射线的方向限制在正方向以内:
class hittable {
public:
virtual bool hit(const ray& r, double t_min, double t_max, hit_record& rec) const = 0;
};存储交叉点的信息
hittable 抽象类还会用到交叉点的信息;为了方便,我们将其以对象的形式存储:
struct hit_record {
point3 p;
vec3 normal;
double t;
};制定对圆的交叉检测
现在我们拥有了 hittale 类,就可以定义专属与圆的交叉方法了。实现上,我们继承 hittable 类,并对虚函数 hit() 进行重写:
bool hit(const Ray &r, double t_min, double t_max, hit_record &rec) const override;rec.t = root;
rec.p = r.at(rec.t);
rec.normal = (rec.p - center) / radius;正面与背面
法线的设计有两种方式。
- 法线的方向与以圆心起始到射线相交点的向量方向一致。也就是说,如果相交的外置在表面外部,则法线与射线的方向相反;反之则方向相同。
- 第二种方式则是始终保持法线与射线相反。
选择使用哪种方式决定了怎样去描述内外都需要渲染的材质,比如双面的纸张,玻璃球等等。
两种设计方式的区别
- 第一种设计方式需要判断射线在表面的内侧还是外侧。这一点可以通过与指向外部的法线进行点积进行判断
if (dot(ray_direction, outward_normal) > 0.0) {
// ray is inside the sphere
...
} else {
// ray is outside the sphere
...
}- 第二种设计方式也需要样验证射线与法线的方向是否一致:
- 如果点积结果大于 0,证明方向相同,则当前法线应该与指向外部的法线方向相反;该表面为内部表面
- 反之,则不用反转,该表面为外部表面
我们通过一个状态变量来保存表面属于内部还是外部:
bool front_face;
if (dot(ray_direction, outward_normal) > 0.0) {
// ray is inside the sphere
normal = -outward_normal;
front_face = false;
} else {
// ray is outside the sphere
normal = outward_normal;
front_face = true;
}这两种设计方式的区别在于希望在哪个时期检测当前表面处于外部还是内部。第一种方法通常在几何相交检测的时期使用,第二种方法则是在计算颜色的时候使用(本教程使用的是该版本)
第二种方式的实现
- 添加
front_face变量与成员函数set_face_normal到hit_record类中,用于存储表面的位置信息和管理法线信息 - 在圆的相交检测中,需要将上述的结果进行存储
管理多个可碰撞的对象
之前我们提到过 hittable 抽象类。该类的主要作用是用于不同类型以及不同数量的可相交物体。文中的 hittbale_list 类继承自 hittbale 类,用于对多个对象进行管理。其设计的使用到的主要 C++ 内容有:
- 智能指针
- vector
数据对象为:
shared_ptr<vector<hittable> >
主要的操作函数有:
- 添加函数
add,通过vector::push_back()实现 - 清空函数
clear,通过shared_ptr的成员clear实现 hit的重写版本,该重写版本将循环访问几何体列表中的所有对象,并调用其自身的hit()重写版本进行交叉检测,并返回是否相交的信息。如果存在相交,则将射线的范围上限设置到该相交点,并存储该点的所有信息。
这里范围上限(cloeest_so_far)的更新是一个逐渐更新的过程。其初始值为我们指定的 t_max(实例中是无穷大);当发生相交后,该上限就会被当前相交点的 t 值更新;这样做的话,射线照射的范围就会逐渐变小。
什么要这么做?
这么做是为了预防我们的相交记录被覆盖掉。当场景中存在多个远近不同的物体时,如果不限制射线的范围,当照射完近处的物体后,假设射线与远处的物体相交,则射线在远处物体上的相交记录将覆盖掉近处物体的相交记录。由于我们的着色是按照相交记录进行的,因此不限制距离的着色将导致位置处于前方的物体会被后方的物体遮挡(后面的实现中,使用了一个远处的大球做地面,可以试试如果一值使用 t_max 做扫描上限会有什么样的渲染结果)
具体算法查看 Fundamentals of Computer Graphics 4.4.4 Intersecting a Group of Objects
数学常量与 Utility 的管理
rtweekend.h 用于存储一些常见的数学常量,工具函数,常用头文件,以及一些 using。 几个比较重要的成员:
- 无限大
<limit> - 圆周率
- 角度与弧度的转换
main 文件中的对应修改[6.7.]
物体列表的创建
使用 hittable_list 对象 world 对场景中的物体进行管理:
hittable_list world;
world.add(make_shared<sphere>(point3(0,0,-1), 0.5));
world.add(make_shared<sphere>(point3(0,-100.5,-1), 100)); //groundray_color 的修改
调用 hittable_list 的成员 hit 对场景中所有的物体进行扫描,如果法线相交则返回以相交点法线为基础的,标准化后的 rgb 颜色;没有相交的点则根据之前的设置,以射线的 y 方向作为颜色基础进行背景渲染。关键代码如下:
hit_record rec;
if (world.hit(r, 0, infinity, rec)) {
return 0.5 * (rec.normal + color(1,1,1));
}Anti-aliasing
之前的算法以像素为单位,因此会在几何体边缘的部分有非常明显的边界,也就是所谓的锯齿(jaggies)。在实际应用中,我们希望通过对边界部分的前景和背景进行像素颜色的中和,获得比较柔和的渐变,从而达到消除锯齿的效果。本节中的抗锯齿技术原理非常简单:
- 以像素的位置为中心,随机对附近位置的点进行颜色计算(采样)
- 将这些点(sampled point)的颜色值累加到像素上
- 使用累加值除以采样点的数量(平均),即可得到最后的混合效果
该技术被称为 Super Sampling,是 Box filtering 抗锯齿技术中最简单的一种,指简单粗暴的对每个点都进行指定采样数量的计算,最后以平均的方式获得最后的着色值。
更多请参考:Fundamental of Computer Graphics Chp.9.3 Simple Anti-aliasing
随机数 Utilities
对采样点位置的选择通常通过附加随机数的方式来选择。C 库中有 <cstlib> 的 rand() 可以使用:
#include <cstdlib>
...
inline double random_double() {
// Returns a random real in [0,1).
return rand() / (RAND_MAX + 1.0);
}
inline double random_double(double min, double max) {
// Returns a random real in [min,max).
return min + (max-min)*random_double();
}<random> 中:
#include <random>
inline double random_double() {
static std::uniform_real_distribution<double> distribution(0.0, 1.0);
static std::mt19937 generator;
return distribution(generator);
}生成像素的采样点
将 camera 改变为 class 对象
直接将 main.cc 中的代码抄过去即可。主要的数据成员有:
point3 origin;
point3 lower_left_corner;
vec3 horizontal;
vec3 vertical;get_ray(),可以通过 uv 坐标来获取指向该点的射线。由于接下来的像素采样点是通过 uv 坐标来着色的,因此这个函数会被应用到像素着色值的累加中:
ray get_ray(double u, double v) const {
return ray(origin, lower_left_corner + u*horizontal + v*vertical - origin);
}write_color 函数的改变[7.2]
本节中,write_color() 函数需要承担两个任务:
- 对累加的着色值进行平均
- 将平均后的结果转移至 [0,256) 区间内
首先是平均着色值的操作。最终的着色值等于累加值除以采样点的个数,因此 write_color() 需要引进采样点的个数来完成平均操作:
void write_color(std::ostream &out, color pixel_color, int samples_per_pixel)
{
....
// Divide the color by the number of samples.
auto scale = 1.0 / samples_per_pixel;
r *= scale;
....
}[0,256) 这个区间中;本节中使用了与 256 相乘的实现方式,因此得到的颜色值必须被限制在 [0,1] 之间。这里需要实现一个 clamp 函数来完成限制操作:
inline double clamp(double x, double min, double max) {
if (x < min) return min;
if (x > max) return max;
return x;
}out << static_cast<int>(256 * clamp(r, 0.0, 0.999));
....main 文件中的对应修改[7.2.]
main 文件中主要的改动是在每个像素点下增加了一层循环,用于计算采样点的着色值。整个过程如下:
- 对每个像素点的颜色进行初始化
- 以指定采样数作为循环上限确定循环次数
- 在每一次循环中,添加随机值像素点的
uv坐标上,以此作为采样点坐标 - 获取到该采样点的射线
- 对该采样点进行着色,并将结果累加到像素点的着色值上
- 最后将得到的累加颜色值输出,交由
write_color()函数进行最终的平均,以及输出处理
for (int j = image_height-1; j >= 0; --j) {
std::cerr << "\rScanlines remaining: " << j << ' ' << std::flush;
for (int i = 0; i < image_width; ++i) {
color pixel_color(0, 0, 0);
for (int s = 0; s < samples_per_pixel; ++s) {
auto u = (i + random_double()) / (image_width-1);
auto v = (j + random_double()) / (image_height-1);
ray r = cam.get_ray(u, v);
pixel_color += ray_color(r, world);
}
write_color(std::cout, pixel_color, samples_per_pixel);
}
}Diffuse Materials
材质与几何模型绑定的方式有两种:
- 混合(分离): 材质可以赋予多个的同类型几何体,反之亦然
- 紧密绑定
本教程采取第一种方式。
漫反射的简单原理
漫反射的主要过程可以描述为:
- 射线从相机出发
- 当射线击中某个物体时,交叉点将成为下一次射线的发射源
- 二次(N次)射线的发射方向是随机的(具体取决于模型)
漫反射材质的特点
- 漫反射材质不会发光
- 漫反射的颜色会根据材质内在的颜色而改变
- 漫反射的方向是随机的
- 漫反射材质会吸收一部分光线。表面越暗,吸收的越多
确定次级射线的方向
尽管次级射线的方向是随机的,但实际上根据模型的不同,射线方向的决定还是会或多或少的受到一些影响。本教程中介绍了两种模型:
- Ideal Lambertain
- 射线的方向均匀分布以碰撞点为中心的在整个半球上
射线的着色方式
无论射线的方向是如何确定的,次级射线的着色都可以被理解为如下的过程:
- 从碰撞点出发
- 如果与下个物体碰撞,则从该物体上的碰撞点继续产生新的次级射线
- 只有当次级射线没有与物体碰撞时,才会停止形成新射线
因此,次级射线的发射可以被认为是一个递归的过程。每一次射线的发射都实在调用 ray_color() 这个函数,而结束条件为射线未击中任何几何体。该判断可以交由对应几何体的 hit() 函数来执行。
基于 Ideal Lambertian 的实现
Ideal Lambertian 被定义为一种效果类似于 ”matte“ 的漫反射表面(更多定义可以查看 fundamental of comupter graphics 5.2.1 小节)。这种表面产生的次级射线的方向会以如下的策略来决定:
- 以碰撞点
P作为起点 - 在
P朝向当前碰撞表面的法线方向上,定义一个与当前表面相切,且过P点的单位球 - 可知该单位球的球心为
P + N,N为法线 - 随后以该球体积作为范围进行随机点
S的生成(位置取决于筛选的策略) - 最后,次级射线的方向将被定义为
P到S的向量,也就是S - P
书中提到了两个点 P+N 与 P-N。这两个点实际上一个处于碰撞表面的外部,而另一个处于内部。在应用中,我们希望次级射线的方向与法线处于相似的方向上。
使用 rejection method 筛选随机点
随机点是一个 3D 向量。我们可以利用之前实现的 random_double() 函数在 X, Y, Z 三个方向上进行随机,将三个方向的 magnitude 都控制在 $[0,1]$ 之间,就可以得到一个边长为 1 正方体的取点范围。然后,利用生成的点与单位球球心的距离与单位球的半径进行比较,即可筛选出处于球内部的随机点。这种方法被称为 Rejection method:
vec3 random_in_unit_sphere() {
while (true) {
auto p = vec3::random(-1,1);
if (p.length_squared() >= 1) continue;
return p;
}
}为次级射线指定最大反射次数
由于次级射线的过程是以递归的形式来实现,当射线反射的次数过多时,很可能会造成栈内存的不足。实现中,我们需要为射线指定一个最大反射次数,来作为该递归的另外一个终结条件:
//in ray_color() function
//If we've exceeded the ray bounce limit, no more light is gathered.
if (depth <= 0)
return color(0,0,0);main 文件中的对应修改[8.2]
ray_color()将以递归的方式进行着色target代表了单位球内的任意随机点,ray通过该点与碰撞点p形成新的射线ray_color()中添加了最大反射次数max_depth作为额外的递归结束条件- 次级射线的着色值为之前
0.5倍,也就是每折射一次被吸收一半 - 其他使用
ray_color()的地方都应该修改对应的参数列表
color ray_color(const ray& r, const hittable& world, int depth) {
hit_record rec;
// If we've exceeded the ray bounce limit, no more light is gathered.
if (depth <= 0)
return color(0,0,0);
if (world.hit(r, 0, infinity, rec)) {
point3 target = rec.p + rec.normal + random_in_unit_sphere();
return 0.5 * ray_color(ray(rec.p, target - rec.p), world, depth-1);
}改进1:矫正 Gamma
上面的代码运行后,得到的结果非常暗,这是因为我们的图片浏览器认为该图像是 Gamma 正确的,而实际上并没有。Gamma 校正通常以下面的公式进行:
$$Gamma \, N = Value^{\frac{1}{N}}$$
书中使用了 Gamma 2.0 的标准,因此需要改写 write_color 函数中的 rgb 值:
// Divide the color by the number of samples and gamma-correct for gamma=2.0.
auto scale = 1.0 / samples_per_pixel;
r = sqrt(scale * r);
g = sqrt(scale * g);
b = sqrt(scale * b);改进2:处理精度带来的 shadow-acne
理论上我们将碰撞点作为次级射线的起点时,其位移 t 应等于 0。但由于精度原因,当相交发生的时候,记录在相交点中的 t 通常会相对 0 产生一些细微的误差,比如 t = -0.00000001。当这种情况发生的时候,我们的物体表面会形成一些黑点,这种现象被称为 Shadow-Acne。
产生这种错误的原因是次级射线与当前表面发生了相交,也就是所谓的自相交(self-intersection)。具体的来说:
- 理想状态下,射线与表面相交与
t=0时。以此为基础,相交点的位置正好处于表面上 - 由于
t的误差原因,如果t为负,实际上的相交点的位置会处于被相交物体的内部 - 因此,以该实际相交点作为起点的射线,会马上与当前的表面发生碰撞并着色
解决方案有两种:
- 提高精度
- 将碰撞点的最小值
tmin稍微增加一点点,保证相交点不会因为误差的原因而处于被碰撞物体的内部。该值被称为 Shadow Bias,可以根据场景的不同来对其进行具体的调整。
本书的实现将 tmin 提高到了 0.001:
if (world.hit(r, 0.001, infinity, rec)) {
//....
}True Lambertain Reflection
Rejection method 是以法线的方向为基础生成的随机点的。其产生的分布并不是很均匀,而是大部分偏向于法线的方向。总的来说,假设射线方向与法线的夹角为 $\phi$,那么 Rejection method 产生的点的分布 scale 是 $cos^3(\phi)$。
对于 Ideal Lambertain 来说,其分布 scale 为 $cos(\phi)$。该方法生成的点离法线的距离近的机率更高,但点的分布也更加均匀。该方法通过将随机点控制在单位球的表面进行生成来实现。代码上来说,我们对 Rejection method 产生的随机点进行标准化,即可达到目的:
inline vec3 random_in_unit_sphere() {
...
}
vec3 random_unit_vector() {
return unit_vector(random_in_unit_sphere());
}
可以看出来:
- Ture Lambertain 方法产生的阴影更浅
- Ture Lamberrtain 方案下,小球与背景大球都变得更亮了
这是因为射线以一种更加均匀的方式进行了发射;这说明偏向法线方向的射线变少了,而该现象会导致两个结果:
- 参与向上反射的次级射线变少,因此阴影会更浅
- 偏向摄像机的射线更多,因此得到的渲染结果会更加明亮(在阴影区尤其明显)
额外的实现方法
除了 ideal Lambertian 模型,还有一种更直观的对 Ideal Lambertian 的近似模型(但其概率分布已经被证明是不正确的)。这种直观的模型认为次级射线的方向在所有的,相对于碰撞点的角度上,都应该均匀的分布(其分布区域实际上是一个半球),而不是依赖于法线来进行分布控制。因此,该随机方式只需要保证射线的方向与法线的方向同向(点积为正)即可:
vec3 random_in_hemisphere(const vec3& normal) {
vec3 in_unit_sphere = random_in_unit_sphere();
if (dot(in_unit_sphere, normal) > 0.0) // In the same hemisphere as the normal
return in_unit_sphere;
else
return -in_unit_sphere;
}point3 target = rec.p + random_in_hemisphere(rec.normal);
Metal
材质的抽象类
材质在实现上有两种类型:
- 大而全的通用材质
- 抽象自材质基类的特定材质
本文采取第二种实现方式。总的来说,所有的材质都需要实现两个基础功能:
- 生成反射的射线(或着说是吸收一部分射线)
- 控制反射光线的被吸收量(Attenuation)
简单的实现如下:
class material {
public:
virtual bool scatter(
const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
) const = 0;
};sactter() 函数会接收射线,根据衰减值返回射线,并将相关的信息存储到 hit_record 对象中:
描述射线与对象相交的数据结构
本课程中,射线与表面相交的相关信息都存储于 hit_record 对象中。由于光线的反射与衰减是通过材质来决定的,因此对应表面的材质信息也需要存储到该对象中,供之后的 ray_color() 着色使用。材质信息通过智能指针来管理:
class material;
//....
struct hit_record
{
//....
shared_ptr<material> mat_ptr;
}对应构造函数的修改
当射线与表面相交时,hit_record 中的信息将被更新。本课中的表面均为球体,因此需要在球体的信息中附带其材质的信息。需要修改的有三项:
- 构造函数的材质参数,用于指定该球体的材质
sphere(point3 cen, double r, shared_ptr<material> m)
: center(cen), radius(r), mat_ptr(m) {};- 球体表面类
sphere中的材质数据成员(由 shared_ptr 管理)
shared_ptr<material> mat_ptr;sphere::hit需要在碰撞发生的时候将表面的材质信息交与hit_record
rec.mat_ptr = mat_ptr;光线散射与反射的模型
这一节实际上是在实现具体的材质。散射的射线强度可以由几种方式来实现:
- 直接使用 reflectance $R$ 作为衰减率
- 使用 $1-R$ 作为射线的被吸收比
- 上述两者混用
除此之外,我们还可以让散射的衰减带有一定概率:引入概率值 $p$,用衰减率除以该值的结果作为新的衰减率,也就是 albedo / p。
Lambertain 类:散射的处理
需要实现的有两个部分:
- 成员
albedo,存储该材质的射线衰减率 - 重写函数
scatter,为当前材质指定射线生成的规则
class lambertian : public material {
public:
lambertian(const color& a) : albedo(a) {}
virtual bool scatter(
const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
) const override {
auto scatter_direction = rec.normal + random_unit_vector();
scattered = ray(rec.p, scatter_direction);
attenuation = albedo;
return true;
}
public:
color albedo;
};
scatter_direction = rec.normal + random_unit_vector();
这一行是之前 true lambertian 实现中 target 的简化版本。
处理散射方向为零向量的情况
当 random_unit_vector() 生成的向量与 rec.normal 正好相反时,散射的方向将会得到一个零向量。这种情况将会导致一些问题(infinities ,NaNs),因此需要作出处理。为此,首先需要定义一个工具函数 near_zero() 判断得到的向量是否非常接近零向量:
//in vec3.h
bool near_zero() const {
// Return true if the vector is close to zero in all dimensions.
const auto s = 1e-8;
return (fabs(e[0]) < s) && (fabs(e[1]) < s) && (fabs(e[2]) < s);
}lambertain 类中的散射方向 scatter_direction 需要先交由该函数判断。如果接近零向量,则直接将方向设置为法线方向:
// Catch degenerate scatter direction
if (scatter_direction.near_zero())
scatter_direction = rec.normal;镜面反射
与漫反射不同,光滑的金属产生的是镜面反射(Mirrored reflection)。镜面反射产生的射线方向与大小可由下图的关系计算出:
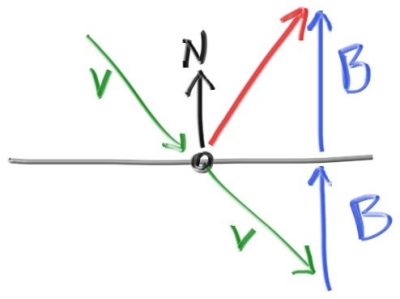
由图可知:
- 镜面反射生成的射线方向为: $v + 2 \cdot b$
- 镜面反射射线的 magnitude 为:$-v \cdot n$
依据点积的结合律,该射线可以表示为: $$ v + 2 * dot(-v, n) \Longrightarrow v - 2 *dot(v, n) $$ 实现:
//in vec3.h
vec3 reflect(const vec3& v, const vec3& n) {
return v - 2*dot(v,n)*n;
}metal 类
metal 类与 lambertain 类的结构类似,也需要重写 scatter 函数和添加衰减率的成员。与 lambertain 不同的是,metal 生成的射线将按照镜面反射的规则来生成:
class metal : public material {
public:
metal(const color& a) : albedo(a) {}
virtual bool scatter(
const ray& r_in, const hit_record& rec, color& attenuation, ray& scattered
) const override {
//scatter direction
vec3 reflected = reflect(unit_vector(r_in.direction()), rec.normal);
//scatter ray
scattered = ray(rec.p, reflected);
attenuation = albedo;
return (dot(scattered.direction(), rec.normal) > 0);
}
public:
color albedo;
};模糊镜面反射
镜面反射的结果可以通过随机偏离反射射线的方向来进行模糊,达到一种类似不光滑表面金属的反射效果。我们将这种反射称为模糊镜面反射(Fuzzy Reflection)。反射射线方向的偏离实现与 true lambertain 类似,也是使用与相交点相切的单位球来生成随机的射线方向。
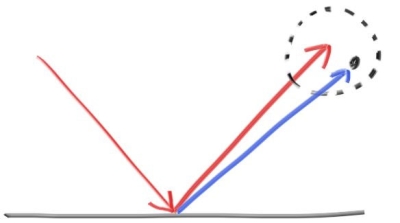
实现中,metal 类添加了 fuzz 成员作为偏离的系数(越大越模糊)。该系数与 random_in_unit_sphere() 函数一起决定了反射射线最终的偏离量:
//cstr
metal(const color& a, double f) : albedo(a), fuzz(f < 1 ? f : 1) {}
//scattered ray with fuzzy reflection
scattered = ray(rec.p, reflected + fuzz*random_in_unit_sphere());main 文件中的对应修改[9.6]
ray_color()
由于我们已经将 material 抽象化,因此需要使用指针进行对应材质的调用。此处我们允许自行指定材质的衰减率:
if (world.hit(r, 0.001, infinity, rec)) {
ray scattered;
color attenuation;
if (rec.mat_ptr->scatter(r, rec, attenuation, scattered))
return attenuation * ray_color(scattered, world, depth-1);
return color(0,0,0);
}
之前一直不太明白为什么 scatter 都要返回一个 bool,此处实际上给出了解答:只有在反射射线与法线的方向同向的时候,才会进行下一步的反射;否则将直接作为阴影处理。
场景的修改
- 改变了背景大球的颜色
- 新增一左一右两球,材质为 metal
- 改变了中间球的颜色
- 模糊镜面反射版本需要提供额外的
fuzz值
auto material_ground = make_shared<lambertian>(color(0.8, 0.8, 0.0));
auto material_center = make_shared<lambertian>(color(0.7, 0.3, 0.3));
auto material_left = make_shared<metal>(color(0.8, 0.8, 0.8));
auto material_right = make_shared<metal>(color(0.8, 0.6, 0.2));
world.add(make_shared<sphere>(point3( 0.0, -100.5, -1.0), 100.0, material_ground));
world.add(make_shared<sphere>(point3( 0.0, 0.0, -1.0), 0.5, material_center));
world.add(make_shared<sphere>(point3(-1.0, 0.0, -1.0), 0.5, material_left));
world.add(make_shared<sphere>(point3( 1.0, 0.0, -1.0), 0.5, material_right));