Boolean Arithmetic and the ALU

Week 2 notes

Binary Numbers

二进制数以 0，1 的组合表示各式各样的数据：n 位二级制数拥有 $2^n$ 的组合数量。

二进制表示数字

Binary to Decimal

二级制按照如下的规则转化为十进制：

从左到右，从 0 开始，每一位的权为 $2^n$
十进制的结果等于二进制数的带权和

比如下面的例子, 101 转化的的结果是 5：

也就是如果有 k 位 Bit,最大能表达的数字为：

$$ 1 + 2 + 4 +...+2^{k-1} = 2^k - 1 $$

Fixed word size

计算机中字的长度是有限的，因此表示的范围也是有限的。理想情况下，一个 8 位的字可以表示 $2^8 = 256$ 个数字；但实际上，如果需要表示负数，那么 8 位的其中一位就会作为符号位，这样 8 bit 只能表示 0-127

Decimal to Binary

按之前转化的逆顺序：

找出当前 10 进制中最大的，可以通过 2^n 计算出的数
从当前数中减去该数
重复上面两步，直到只剩 1($2^0$)

这个过程相当于是在还原二级制构造十进制的过程。因此，之前能找出来的数证明其对应的 Bit 上都是 1，反之都是 0。以 87 位例：

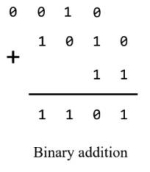
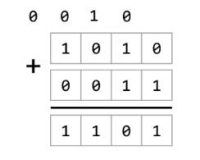
Binary Addition

二进制的加法与十进制类似，按位相加：

如果遇到 1+1 的情况，则进位。进位是逢 2 进 1：

overflow

如果最后一位相加也需要进位，此时结果长度超出了字的长度。我们称该情况为加法溢出（overflow）。解决的方式是：忽略所有额外的进位。从计算机的角度来考虑，如果加法超出了字长的限制，那么我们做的加法，就不再是真正的加法了。

Adder 的设计

从这个思路出发，Adder 的设计分为：

Half Adder：负责两个 Bit 的相加
Full Adder：负责三个 Bit，即两个 Bit 与 carry 的相加

Half Adder

Half Adder 完成的工作是将两个 Bits 相加。那么：

输入：两个 bits x, y
输出：一个 bit （和），一个 carry（进位）

需要注意的是，两个 Bits 相加只和当前的 Bit 有关。只要是 1 + 1，那么进位就是 1，结果就是 0。因此，我们可以得到如下的真值表：

Full Adder

Full Adder 完成的工作是将两个 Bits 与 carry 位相加：

输入：bit a, b, c
输出：sum, carry

其真值表也非常容易得到：

Multi-bit Adder(16bits)

这个 adder 由一系列的 half adder 和 full adder 组成。准确的来说，是 15 个 full adder 与 1 个（最右边的）half adder 组合在一起，组成了 16 bits 的，带进位的加法计算器。

Negative Numbers

表示负数的方式有三种：

signbit（原码）
Complement （补码）

Signed Bit（原码）

这种方式使用二进制的最高位作为符号位，以此来区分正负数。其他位不变，比如：

000 -> 0 100 -> -0
001 -> 1 101 -> -1
010 -> 2 110 -> -2
011 -> 3 111 -> -3

这种方法通常不会采用，有几个大的缺点：

-0 的定义，它与 0 的区别无法解释
加减法无法处理。比如 1 + (-1)，也就是 001 + 101, 结果是 110，为 -2, 不是 0

2's Complement（补码）

这种方式下，所有的负数都用 bits 可以表示数字的总数来减去负数对应的整数，即： $$2^n-x$$ 比如：

// 4 bits, total numbers: 2^4 = 16
 3 -> 0011
// decimal
-3 -> 16 - 3 = 13 -> 2^3 + 2^2 + 2^0 -> 1101

这种情况下，正数的表达范围为 $[0, 2^{n-1} - 1]$，负数的表达范围为 $[-1, -2^{n-1}]$

补码的优势

使用补码表示负数可以将负数的加法（减法）转化为加法：

根据上面的例子，这个过程分为了三步：

求出负数的补码结果（正数，比如 $-2 = 16 - 2 = 14$）
将得到的正数转换为二级制相加
当存在 overflow 时，溢出位将被自动丢弃，比如此处 $14+13=27$，丢弃溢出位后结果为 $27-16 = 11$
$11$ 是以补码形式，根据公式，负数的表现形式为：$2^4 - positiveNumber = 11$。可以得到正数的值为 $5$，因此 $11$ 对应的负数为 $-5$

计算 -x

上面计算负数的过程是将二进制转化为十进制来进行的。实际上，利用补码公式的变形，就可以很轻松的用二进制直接计算负数： $$ 2^n-x = 1 +(2^n-1) -x $$ 观察一下上面的变形，可以发现：

1 -> 1
2^n - 1 -> 11111....1111

那么也就是说，$-x$ 的实际结果，等于所有 bits 都是 $1$ 的数减去 $x$ 对应的二进制，再加上一。比如 $-2$，如果以 4 bits 的二进制表示，就是：

16 - 2
-> 15 - 2 + 1
-> 1111 - 0010 + 1
-> 1101 + 1
-> 1110

从形式上来看，$x$ 的负数结果实际上是直接将 $x$ 的二进制按位翻转后再加上一得到的。

Arithmetic Logic Unit

Arithmetic Logic Unit (ALU) 在冯诺依曼架构中充当了很重要的角色。具体的来说：

ALU 扮演的是函数的角色，也就是接受输入，然后按指定的方法计算结果的的计算单元。
ALU 对应的函数是提前定义的，算术或逻辑运算的一种（或是这两者的组合）

ALU 的设计在硬件和软件中均可实现。硬件实现下，ALU 的速度会更快，但成本会更高。

实例：Hack ALU

本课例子（HACK ALU）：

接收两个 16 bits 的输入
得到一个 16 bits 的输出和两个 1 bits 的输出。
实现了一系列的（总共18个）基础函数
调用哪个函数通过结构图正上方的 6 个 1 bit 的输入来决定。

其结构图如下：

目录