Applications of Differentiation

MITx: 18.01.1x Calculus 1A notes

一个函数的图像在不同的区间内可能呈现出不同的走势：比如上扬或者下挫；而我们都知道导数可以用来描述函数图像走势。因此我们可以利用导数来大致的判断出函数的图像变化。

在描述函数的图像走势的过程中，最重要的是确定函数在什么地方变化。这个变化的地方往往是一个点；我们把这个点称为 Critical Points。

Critical Points 需要分情况讨论：

• 如果该点是平滑的接入函数图像的时候，那么该点的导数应该是与 $x$ 轴平行的，也就是 $f'(x) = 0$。
• 如果该点是断点，或者是一个角（不平滑），那么该点的导数应该是不存在的。

这两种情况下，该点都可以被称为 critical points

有了 Critical Points，我们在很大程度上就能判断函数图像的走势了。但光靠 Critical Points 还不够。按照 Critical Points 的定义，我们会发现有一些 Critical Points 实际上是没什么用的，比如下图这样的点：



这样的点符合 Critical Points 的定义，但对函数的走势描述并没有太多的作用。我们需要的点，应该是函数走势变化明显的点，是一些函数走势状态转换的点，比如函数从上升转化为下降的中间点。

我们来看看这样的点长什么样：

如果一个函数从下降变化为上升，那么这个函数的图像很可能就看起来就是下图这样的：



反过来，如果一个函数从上升变化为下降，那么这个函数的图像很可能看起来就是下图这样的：

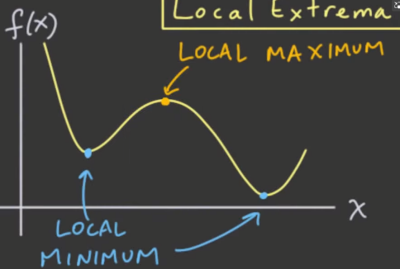
从函数的图像上我们能很明显的看出来，下降变化为上升的情况，变换点在局部区域内的值是最大的；而上升变化为下降的情况，变换点在局部区域内的值是最小的。

因此，我们称第一种变换点为局部最大点（Local Maxima），而称第二种变换点为局部最小点（Local Minima）。而如果我们确定了这样的点，我们就能很容易的画出函数的大概图像了。

明显的是，在局部最大点的左边，函数的导数是大于 $0$ 的；而在该点的右边，函数的导数小于 $0$ 。对于局部最小点，导数的正负正好相反。因此，我们可以得出局部最大点和最小点的定义：

Suppose the function $f(x)$ is continuous at $x=a$ and has a critical point at $x=a$.
$f$ has a local minimum at $x=a$ if $f'(x)<0$ just to the left of $a$ and $f'(x)>0$ just to the right of $a$.
$f$ has a local maximum at $x=a$ if $f'(x)>0$ just to the left of $a$ and $f'(x)<0$ just to the right of $a$.
The point $x=a$ is neither a local minimum nor a local maximum of $f$ if $f'(x)$ has the same sign just to the left of $a$ and just to the right of $a$.

我们把以上的这种判别局部最大点 / 最小点的方法，称为 The First Derivative Test。

The First Derivative Test 是一种很好用的方法，但应用这种测试有一个非常重要的条件：判断导数正负的点与局部最大 / 最小点之间，不能再有另外的 Critical Points 。因为，如果有了额外的 Critical Points ，那么这个区间内导数的正负，就不一定了。

因此，如果不能确定某个区间内 Critical Points 的具体位置与数量，那么我们就不能用 The First Derivative Test 来判断局部最大 / 最小点了。这种情况下，我们可以利用二阶导数的性质来判断某个点附近的函数图像。

The Second Derivative Test 正式定义如下：

Suppose that $x=a$ is a critical point of $f$, with $f'(a)=0 $.
If $f''(a)>0$ , then $f$ has a local minimum at $x=a$ .
If $f''(a)<0$ , then $f$ has a local maximum at $x=a$ .
If $f''(a)=0$ , or does not exist, then the test is inconclusive — there might be a local maximum, or a local minimum, or neithe

二阶导数除了可以判断局部最小 / 最大点以外，还可以判断凹凸性的变化。当二阶导数在某点的左侧和右侧正负发生了改变，那么我们就称该点为拐点（Inflection point）。这个点也是用于描述函数图像的重要条件之一。

除了研究指定区间内的函数图像，有时候我们也需要研究函数的趋势，特别是趋向于无穷的时候。比如研究算法的复杂度，就需要研究算法的复杂度会无限趋近于一个什么样的值。这样的应用需要我们能够判断出函数是逼近某一个值的，还是没有边界的递增或者递减的。

来看下面一个例子：
$$ f(x) = \frac{x}{(\ln x)^2} $$
如果要画出上面这个函数在其整个定义域的图像，应该怎么做呢？

我们可以先按照上一节的一些策略来对这个函数进行分析。不过在这些分析之前，我我们需要先确定该函数的定义域：

• 因为有 $lnx$，因此 $x \in (0, +\infty)$
• 因为 $lnx \neq 0$，因此 $x \neq 1$，所以实际上该函数的定义域为：$(0,1) \cup (1, +\infty)$

这两步实际上找出了绘制函数图像说比较重要的两种点：End points 和 Discontinuities。更重要的是，我们不但需要找到这样的点，而且需要评估当 $x$ 无限趋近于这些点时，函数的值（也就是函数在该点的极限值）。有了这些信息，我们才知道函数在这些点附近的趋势。

来看看本例中的这两种点。该函数的 End points 是 $0$ 和 $+\infty$，也就是函数定义域的边界；而 Discontinuities 是 $1$，是函数中未定义的点。

对于 End points 来说，要了解其图像的走势，只需要对左边的点计算其右极限，对右边的点计算器左极限就可以了。应用到本例中则有： \begin{align} f(0^+) = \frac{0^+}{ln(0^+)^2} = \frac{0^+}{(-\infty)^2} = 0\\\\ f(\infty) = \frac{\infty}{(\infty)^2} = \frac{\infty}{\infty} = \infty \end{align} 对于第二个 End points 处函数的值，我们发现结果变成了 $\displaystyle \frac{\infty}{\infty}$ 这样的形式。我们称这样的形式为 Indeterminate Form；也就是说，这样的形式是不能直接判断极限是多少的，需要做进一步的处理。在这里，我们通过观察函数的分子分母变化的快慢得出结论：该函数在正无穷处的值为正无穷。

Discontinuities 附近的函数值也是测绘函数的必要条件之一。因为这种类型的点往往处于函数图像的中间，所以通常我们需要对其两端的极限分别进行计算。

本例中，Discontinuities 处于 $x = 1$，因此我们需要计算 $f(1^+)$ 与 $f(1^-)$。因为本函数分母部分为正，而分母为 $x$，所以在 $x=1$ 附近的函数值必然为正。而又因为 $x$ 趋向于 $1$时，$ln(x)$ 的值无论正负，都趋向于 $0$，因此我们有： \begin{align} f(1^+) = \infty\\\\\ f(1^-) = \infty \end{align}

剩下的步骤就是我们之前讨论过的，找出函数的 Critical points 和 Inflection points 了。这两步非常简单，只需要找出 $f' = 0$（或未定义） 和 $f'' = 0$ 的点，并判断导数和二阶导数在对应点左右的正负即可（即第一导数 / 第二导数测试)。本例中可以求出 critical point 为 $x = e^2$，Inflection point $x = e^3$；分别求出对应的导数/二阶导数的递增/递减区间即可。对应点附近的正负如下图：

总的说来，对函数的画图基本可以分为以下四步：

1. 找出函数的定义域
   1. 确定边界点（End points），通常情况下类似于 $x \rightarrow \pm \infty$
   2. 确定所有的断点 （Discontinuities），特别是夹在中间的
2. 找出 Critical points：通过求解 $ f'(x) = 0$，或者观察导数的未定义情况
   1. 判断所有以上的点附近的导数正负情况，通过正负情况判断函数是上升还是下降的。
3. 找出 Inflection points：通过求解 $f''(x) = 0$ 找出。
   1. 判断 Inflection points 附近二阶导数的正负情况，确定函数的凹凸性变化。

在之前的例子中，当我们希望得到 End points 处函数的值时，我们遇到了一种情况：对于 $\displaystyle \lim \limits_{x \rightarrow a} \frac{f(x)}{g(x)}$，我们有：

$$ \begin{array}{l} \displaystyle f(x) \rightarrow \infty\\ \displaystyle g(x) \rightarrow \infty \end{array} \quad \text { as } x \rightarrow a $$
这种形式与另外一种形式 $\displaystyle \frac{0}{0}$ 一起被称之为 Indeterminate Form；该形式意味着我们需要对这种形式的极限进行进一步的判断，才能得出正确的极限结果；当然，这意味着要下更多的功夫。

幸好，前人帮我们解决了这一棘手的问题。通过洛必达法则（L'Hospital's Rule），我们可以迅速的判断出具有不确定形式的极限的值。

根据 Indeterminate Form 的不同，洛必达法则的定义分为两种不同的情况：

对于 $\displaystyle \frac00$ 的形式：

if $$\begin{array}{l} \displaystyle f(x) \rightarrow 0\\ \displaystyle g(x) \rightarrow 0 \end{array} \quad \text { as } x \rightarrow a$$
and the functions $f$ and $g$ are differentiable near the point $x = a$, then limit:


$$\displaystyle \lim _{x \rightarrow a} \frac{f(x)}{g(x)} = \lim _{x \rightarrow a} \frac{f'(x)}{g'(x)}$$
provided that the limit on the right hand side of the equation exists or is $\pm \infty$.

对于 $\displaystyle \frac{\infty}{\infty}$ 的形式：

if $$\begin{array}{l} \displaystyle f(x) \rightarrow \pm \infty \\ \displaystyle g(x) \rightarrow \pm \infty \end{array} \quad \text { as } x \rightarrow a$$
and the functions $f$ and $g$ are differentiable near the point $x=a$, then limit


$$\displaystyle \lim _{x \rightarrow a} \frac{f(x)}{g(x)} = \lim _{x \rightarrow a} \frac{f'(x)}{g'(x)}$$
provided that the right hand limit exists or is $\pm \infty$

$\displaystyle \frac{0}{0}$ 形式的证明非常简单。我们注意到，在 $x \to a$ 时，两个函数均趋向于 $0$，所以有 $\ f(a) = g(a) = 0$（这里需要独立的看待分母分子的函数）。

对于极限$\displaystyle \lim _{x \rightarrow a} \frac{f(x)}{g(x)}$，我们对其分母分子同时除以 $(x-a)$，则有：

$$\displaystyle \lim _{x \rightarrow a} \frac{f(x) / (x-a) }{g(x) / (x-a)}$$
因为 $\ f(a) = g(a) = 0$ ，因此上述极限中的函数可以写成如下形式：

$$\displaystyle \lim _{x \rightarrow a} \frac{f(x) / (x-a) }{g(x) / (x-a)} = \lim _{x \rightarrow a} \frac{\frac{f(x)-f(a)}{(x-a)} } {\frac {g(x) - g(a)} {(x-a)}}$$
根据导数的定义，上面的式子可以直接写成 $\displaystyle \lim _{x \rightarrow a} \frac{f'(x)}{g’(x)}$，得证。

从几何上来说，如果将 $\displaystyle \frac{f(x)} {g(x)}$ 作为一个新的函数，该函数由 $f(x)、g(x)$ 作为变量（也就是一个二元映射），那么 $\displaystyle \frac{0} {0}$ 的形式则可以理解为通过变量 $f(x)、g(x)$ 的和原点的函数图像（Secant line）与 $x$ 轴重合（因为该形式下新函数必过 (0,0)点）。

除了以上提到的两种情况以外，我们有时候还会遇到其他的一些不确定形式，对于这样的情况，我们采取的策略是将其转化为洛必达法则适用的不确定形式。

来看看以下例子：

$$ \displaystyle \lim _{x \to 0^{+}} xlnx $$
这是一个 $0 \cdot \infty$ 的形式。我们可以将 $xlnx$ 直接转化为 $\displaystyle \frac{\infty}{\infty}$ 的形式，即：
$$ \displaystyle xlnx = \frac{lnx}{\frac{1}{x}} $$ 对上面的式子应用洛必达法则，则可以很轻松的求出该函数在当 $x \to 0^+$ 的极限为 $-x$，也就是 $0$。

$\infty - \infty$ 类型处理方法类似，不再赘述。

除了以上的两种不确定形式以外，对于复合函数$f(x)^{g(x)}$，以下的几种情况也是不确定形式：

• $0^0$，也就是 $f(x) \to 0$ 时，$g(x) \to 0$
• $\infty ^0$，也就是 $f(x) \to \infty$，$g(x) \to 0$
• $1^0$，也就是 $f(x) \to 1时$，$g(x) \to 0$

对于以上几种不确定形式（也就是具有 Moving exponents 的形式），我们可以使用自然对数将其转化为可以使用洛必达法则的不确定形式，即：

$$\displaystyle \lim_{x \to a}f(x)^{g(x)} = {\huge e}^{\displaystyle \lim_{x \to a} \frac {ln(f(x))} {1 / g(x)}} $$

洛必达法则适用必须要遵循以下三个准则：

1. 洛必达法则适用对象必须要满足不确定形式 $\displaystyle \frac {0}{0}$ 或者 $\displaystyle \frac {\infty}{\infty}$，每次使用之前必须检查（存在第一次可以用，但之后某一次不可用的情况，因此需要每次使用都检查）
2. 洛必达法则适用对象必须可导（$\displaystyle \frac{f'(x)}{g'(x)}$ 的极限不存在的时候不能使用！）
3. 洛必达不适用于求导不能简化函数的情况。

通过 Local Extrema 我们知道函数很可能在局部走势变化的位置拥有“局部的”最大值或者最小值。那么函数能不能在一个区间上取得最大值或者最小值呢？

来看看以下的三种情况：

情况1，$f(x)$ 在 区间 $[1,4]$ 上没有极大值和极小值：

情况2，$f(x)$ 在 区间 $[1,4]$ 上有多个极大值和一个极小值：



情况3，$f(x)$ 在 区间 $[1,4]$ 上有一个极大值，但没有极小值：

相对于极值，我们把上述这些表示函数在某个区间上的最大最小值，称为最值（Global Extrema）：

1. 第一个例子中，函数在 $x = 2$ 的时候不连续，导致函数的值出现的无穷大和无穷小，因此可以判断是无穷大与无穷小不能作为最值。
2. 第二个例子中，函数拥有多个相等的最大值，因此可以判断最值所在的点可以存在多个。
3. 第三个例子中，函数看起来有最小值；但在最小值的位置，函数没有定义。因此，最值必须是函数上某个存在定义的点。

通过以上的观察，可以发现的是，凡是没有或者缺少最值的函数，他们都有一个共性：不连续。极值定理正是通过该特性来判断最值是否存在的。

极值定理（Extreme Value Theorem）的定义如下：

If $f$ is continuous on a closed interval $[a,b]$, then there are points at which $f$ attains its maximum and its minimum on $[a,b]$.
It is important to note that this is only guaranteed if the interval is finite and closed.

因为最值牵涉到最大、最小值的概念，因此我们不可避免的需要将其与极值起来。我们通常通过 Critical Points 来求函数的局部最大值与最小值，因此它与极值有着千丝万缕的联系。

对于一个定义闭区间内连续的函数，我们可以做出总结的有以下几点：

• Critical Points 不存在的情况下，最值点处于函数区间首尾两端。
• 除开函数首尾两端的点，不是 Critical Points 的点一定不是最值点。
• 即使函数上一个点是 Critical Points 点，它也可能不是最值点（当其并不作为函数趋势变化点的时候，参见1.2）

很显然我们可以得出一个结论：最值要么是极值，要么就位于区间的首尾两端。

因此，在求极值的时候，我们需要分几个步骤：

除了极值定理使用的有限闭区间以外，我们通常还会遇到开区间（半开区间），或者带有无穷的区间。对于这样的区间，我们很可能不能直接将首尾两端的值代入函数计算。对此，我们可以利用极限对该函数的区间边缘值做一个评估。

极值代表了函数在某个区间的上的上限与下限，因此极值可以应用到各种求最大最小值的应用中。一类比较明显的例子就是函数中的变量有明显的关系，但总量固定，需要求这些变量在什么样的比例下函数的值可以达到最大化或者最小化。比如以下的例子：

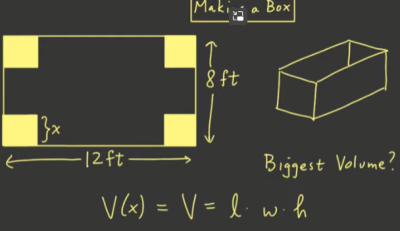
• 一张纸长宽之和固定，求长和宽各位多少时，该纸作出的盒子体积最大。
• 一根定长的线裁成两根，一个做圆一个做正方形，求如何裁线才能使圆和正方形面积之和最大。

这类问题有一个很明显的特征，都是求最值的问题。其最值的函数由几个非独立的变量（也就是可以用一个变量表示所有的变量）组成。因此，为了建立求最值的函数，有几个步骤需要处理：

• 找出一个可以表示所有非独立变量的基础变量，比如下图中角上的正方形的边长 $x$，盒子的长宽高都可以用 $x$ 表示
• 使用基础变量得到求最值的函数
• 根据非独立变量的区间求出基础变量的区间，进而得到最终函数的区间

通过这样的方式，一个拥有区间的函数模型就建立了，我们就可以基于该函数对其求最值。

需要注意的是，我们并不能保证函数在该区间上的连续性，因此必须对该区间上的极大极小值进行有效性判断。

来看一个例子： 问题：一个人吊挂在一根滑绳上移动。滑绳的两端固定，那么这个人会在什么位置停止滑动？

这个问题实际上是在问当滑绳上的重物在什么情况下趋于稳定。物理学告诉我们，当处于滑绳被吊挂状态的最低点时，重物会趋于稳定（停止运动）。那么通过数学，我们可以对该结论进行建模：

假设滑绳的两端为 $0,0$，$a,b$，滑绳的稳定点处于 $x,y$：



那么根据三角关系我们可以得到以下的图：



由于绳索的长度不会发生变化，因此有： $$\sqrt{x^2+y^2} + \sqrt[]{(a-x)^2+(b-y)^2} = constant$$

接下来对上面的式子进行隐式求导：

\begin{align} &\sqrt{x^2+y^2} + \sqrt[]{(a-x)^2+(b-y)^2} = constant \\ \Rightarrow &\frac{x+y\cdot\frac{dy}{dx}}{(x^2+y^2)} -\frac{(a-x)+(b-y)\cdot\frac{dy}{dx}}{\sqrt{(a-x)^2+(b-y)^2}}=0 \end{align}
此时再注意看第一幅图像，因为 $(x,y)$ 是整个重物运动轨迹的最低点；如果将重物的运动轨迹视作函数图像，那么显然 $(x,y)$ 是该函数的 minima，因此过 $(x,y)$ 的切线一定是水平的，也就是 $\frac{dy}{dx}=0$。因此，上式中的 $\frac{dy}{dx}$ 项都可以去掉，即：

$$ \frac{x}{(x^2+y^2)} =\frac{(a-x)}{\sqrt{(a-x)^2+(b-y)^2}} $$
通过观察，上述等式的左右两边，实际上是对应的斜边与竖轴的夹角的正弦函数。这也说明，这两个斜边与竖轴的夹角相等。得知该结论后，我们就可以利用三角关系来计算 $(x,y)$ 的具体位置了。

• Find the closest point to the origin
• Minimize the area of a triangle
• Minimize the surface area of a cylinder

Related Rates 指存在多个变量的情况下，通过给定的关系 rate of change 来推导出另外的关系的过程。

以下是一个的例子：

已知体积基于时间的变化率 $\frac{dV}{dt}$，以及体积与半径的函数 $V = \pi hr^2$，求半径基于时间的变化率$\frac{dr}{dt}$。

我们注意到上面的函数中，左边是 $V$，右边是 $r$，因此如果对两边同时进行求导（隐式求导），那么得到的结果就是 $\frac{dV}{dt}$ 与 $\frac{dr}{dt}$ 之间的关系，即：
$$ \frac{dV}{dt} = \frac{d}{dt}\pi hr^2 $$

由于所求的是 $r$ 基于 $t$ 得关系，因此右边求导需要应用 chain rule，结果是： $$ \frac{d}{dt}\pi hr^2 = 2\cdot\pi h\cdot r \cdot \frac{dr}{dt} $$
之后将 $r$ 的值带入即可得到所求的变化率。

由上面的例子我们可以总结出 Related Rates 问题的一般解决思路：

来看一个典型的应用例子：

有一个正方形的监狱，监狱边长400米。监狱中心有一盏探照灯会将光线打到墙上。该探照灯每分钟旋转两圈。请问，作为一个犯人，是否有>能力在不被灯光照到的情况下到达墙壁？

解题思路： 首先，我们可以画一张草图来数学化这个问题：



这个问题的实质实际上就是在讨论犯人的速度和探照灯的投影在墙上移动的速度。如果人移动的够快，就可以在探照灯的投影到达之前到达墙壁。在这里，我们将探照灯的投射过程考虑一条直线 $z$，探照灯在墙上投影移动的距离记做 $y$，犯人跑动的距离记做 $x$，那么该问题实际上就主要是计算出探照灯在墙上移动速度，即探照灯投影的移动速度，即$\displaystyle \frac{dy}{dt}$。

根据题目中已知的信息，可以得知是探照灯的转动速度。如果令探照灯与逃脱路线的夹角为 $\theta$，那么该速度可以表示为 $\displaystyle \frac{d\theta}{dt}$。因此，问题就转化成了 Related Rates 问题，已知探照灯转动速度，求探照灯的投影的速度。

那么接下来只需要找到这两者的关系（函数）即可。通过对图的观察，可以得出：

$$\frac{y}{200} = tan\theta $$

既然我们要求 $\displaystyle \frac{dy}{dt}$，那么将上面的式子整理一下，然后对左右两边同时微分，既有：

\begin{align} \displaystyle \frac{d}{dt}y &= \frac{d}{dt}200 \cdot tan\theta \\\\\ &=200 \cdot sec^2 \frac{d\theta}{dt} \end{align}

对于函数 $sec^2\theta$，$\theta$ 的值取值范围在 $[\pi/4, -\pi/4]$，算出来的速度在 $1600\pi\quad m/min$ 左右，人的速度是不可能达到这么快的，因此是不能逃脱的。

• Filling a ballon
• Another ladder problem

• 马同学-如何解释洛必达法则？
• 马同学-洛必达法则失效的情况有哪些？