目录
Matrix-Vector Operations
LAFF Week 3 Notes
本章的核心概念主要在于理解矩阵与向量的乘法的意义。矩阵是一种线性变换(映射),那么向量通过变换得到的结果就是一个新的向量,形式上表现为矩阵的列的线性组合。
除此之外,本章还有大量内容关于矩阵的操作、矩阵向量乘法的操作,以及这些内容在计算机中实现,以及优化。
Special Matrices
Partition Matrix into Quadrants
这一点值得在学习所有特殊矩阵之前提出来,因为相较于按列划分矩阵的方式 week2 note 2.1,该划分方法贯穿了绝大多数的矩阵的操作(初始化,矩阵与向量的乘法等等)。我们来看看这种划分是如何进行的:
该方法的核心是将矩阵划分为大的四部分。为了算法设计的方便,又将该四大部分详细划分称了9部分,如下图所示:
<html>
<img src=“/_media/math/linear_algebra/laff/p_m_q_0.svg” width=“400”>
</html>
下面用一个矩阵来作为示例。
第一步迭代:
我们从左上角的 $A_{TL}$ 部分开始遍历。默认情况为 $A_{TL}$ 为没有任何元素。那么很显然,此时的$A_{BR} $ 包含了了所有的矩阵元素,也就是说,$A_{TR}$、$A_{BL}$ 都是没有任何元素的:
<html>
<img src=“/_media/math/linear_algebra/laff/p_m_q_2.svg” width=“200”>
</html>
那么很显然,此时的,作为$A_{BR}$最左上角的一个元素, $a_{00}$ 就是划分图中的 $A_{11}$,也就是本次迭代过程中的 $A_{11}$。
<html>
<img src=“/_media/math/linear_algebra/laff/p_m_q_3.svg” width=“500”>
</html>
这里的 $A_{12}^T$ 实际上就是我们的 $A_{12}$。 因为根据上图,我们发现 $A_{12}$ 划分的区域实际上是一个行向量,因此将其写成 $A_{12}^T$。
中间迭代:
我们继续按上面的分块方法来划分矩阵,那么经过划分的 $A_{BR}$ 则有了新区域,伴随而来的是 $A_{11}$ 等区块又发生了新的改变,如下图:
<html>
<img src=“/_media/math/linear_algebra/laff/p_m_q_4.svg” width=“600”>
</html>
而通过上述的中间迭代,我们可以很顺利的通过这样的迭代方式遍历整个矩阵。
使用这种方式的优势在哪里?目前我们可以看到的是:这种分块的方式可以直接对对角线上的元素进行操作。这对于某些特殊矩阵的算法设计以及操作是非常便利的。
Zero Matrix
零矩阵代表了一种将所有输入向量统统映射到原点的线性变换。零矩阵中所有的元素都为 0,可以记作:
$$
L_0(x) = 0 \,\, \text{for all x} \\
L_0 : \mathbb{R}^n \to \mathbb{R}^m \\
$$
如下的矩阵就是一种零矩阵:
$$
\begin{pmatrix}
0 & 0 & \cdots & 0 \\
0 & 0 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 0 \\
\end{pmatrix}
$$
算法:初始化矩阵为零矩阵
The Identity Matrix
单位矩阵代表了一种不更改原有向量 / 矩阵的线性变换。该矩阵的特点是以左上为起始位置的矩阵对角线上所有的元素为 $1$,矩阵其他部分均为 $0$。该矩阵可以用代数的形式表示为:
$$
L_I (x)=x \,\, \text{for every x} \in \mathbb{R}^n \\
$$
需要注意的是,单位矩阵必须是方阵。
如下是一个单位矩阵的例子:
$$
\begin{pmatrix}
1 & 0 & \cdots & 0 \\
0 & 1 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots &1 \\
\end{pmatrix}
$$
算法:初始化矩阵为单位矩阵
- 将矩阵从列与行两个方向上进行划分(也就是之前提到的象限划分法)。
- 在左上区域 $A_{TL}$ 的行数小于整个矩阵的行数之前,对矩阵对角线上的元素 $a_{11}$ 赋值 $1$,对其上下划分出来的(元素或者向量)进行赋 0 操作。迭代此操作,直到 $A_{TL}$ 的行数与 $A$ 的行数相等为止。
Diagonal matrices
对角矩阵(Diagonal matrices)是一种除了主对角线之外其他元素皆为 0 的矩阵。也就是说,如果将该类矩阵按列分割表示,那么就有:
$$
\text{if} \,\, y = L_D(x) \,\, \text{then} \,\, y_{i} = e_ix_i
$$
因为对角矩阵中只有主对角线上的元素不为 0,因此该矩阵的每列都可以表示成一个 unit basis vector 。因此目标向量 $y$ 的第 $i$ 个分量等于原向量 $x$ 的第 $i$ 个分量与矩阵中第 $i$ 列代表的 unit basis vector 的点积。如下是一个对角矩阵的例子:
$$
\begin{pmatrix}
5 & 0 & \cdots & 0 \\
0 & 12 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots &17 \\
\end{pmatrix}
$$
对角矩阵也必须是方阵。
算法:将矩阵初始化为对角矩阵
Triangular Matrices
三角矩阵 (Triangular Matrices)指其非零系数只在主对角线一侧的矩阵。
三角矩阵存在着一些分支:
- 按照非零系数的位置,又分为上三角矩阵与下三角矩阵。
- 如果三角矩阵的所有非零系数均为 1,那么称该三角矩阵为单位三角矩阵 (Upper triangular Matrices)。
- 如果三角矩阵的主对角线也同时为 0,那么就称该三角矩阵为严格三角矩阵(Strictly triangular Matrices)。
细致的代数定义如下:
 下面是三角矩阵的演示:
下面是三角矩阵的演示:
上三角矩阵:
$$
\begin{pmatrix}
5 & 3 & \cdots & 4 \\
0 & 6 & \cdots & 2 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots &8 \\
\end{pmatrix}
$$
严格上三角矩阵:
$$
\begin{pmatrix}
0 & 3 & \cdots & 4 \\
0 & 0 & \cdots & 2 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots &0 \\
\end{pmatrix}
$$
单位三角矩阵:
$$
\begin{pmatrix}
1 & 1 & \cdots & 1 \\
0 & 1 & \cdots & 1 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots &1 \\
\end{pmatrix}
$$
与之前对角矩阵相同,三角矩阵也是方阵的一种。
算法:初始化矩阵为三角矩阵
初始化三角矩阵的具体操作根据不同的矩阵有不同的操作,但整体步骤是大致相同的:

上面的算法是我们之前提到过的矩阵分割算法。我们只需要在每一个迭代中进行对应的赋值,就能得到对应的三角矩阵。来看看具体的操作:
对上三角矩阵,只需要在每次迭代中对 $A_{10}^T$ 或 $A_{21}$ 所代表的向量赋零即可,也就是:
a10t = 0; %in row
a21 = 0; %in col<html>
<img src=“/_media/math/linear_algebra/laff/p_m_q_tr1.svg” width=“300”>
</html>
严格上三角矩阵只需对对角线元素,即 $A_{11}$ 赋零即可:
a10t = 0; a11 = 0 ; //in row
a21 = 0; a11 = 0; // in cola10t = 0; a11 = 1 ; //in row
a21 = 0; a11 = 1; // in col<html>
<img src=“/_media/math/linear_algebra/laff/p_m_q_tr2.svg” width=“300”>
</html>
Transpose Matrix
转置矩阵(Transpose Matrix)在运算上表现为将原矩阵的行作为新矩阵的列而得到的矩阵。数学上的表现如下:
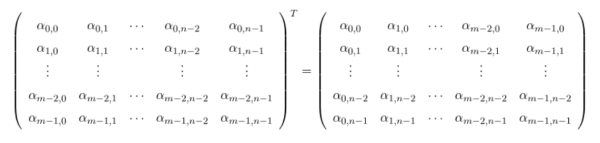
具体的例子可以参考下图:
<html>
<img src=“/_media/math/linear_algebra/laff/p_m_q_t.svg” width=“300”>
</html>
算法:求矩阵的转置矩阵
转置矩阵的性质
- 上下三角矩阵互为转置矩阵
- 单位矩阵的转置依然是单位矩阵
Symmetric Matrices
对称矩阵(Symmetric Matrices)是指原矩阵与目标矩阵相对于主对角线“对称”。数学上的定义如下:
$$A \in \mathbb{R}^{n \times n} \\
\text{A is said to be symmetric if}\,\, A = A^T.$$
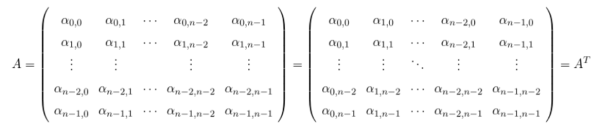
根据定义,原矩阵必须要与其转置矩阵相等才能对称,因此可以判断原矩阵与其对称矩阵必为方阵。
算法:求三角矩阵的对称矩阵
矩阵的对称矩阵是相对于主对角线对称的(转置)。也就是说 ,求三角矩阵的对称矩阵,只需要在每次迭代中将对应区域的元素进行转置即可。下面是求下三角矩阵的对称矩阵算法:

每次迭代中,我们都将下三角矩阵中 $A_{10}^T$ 区域的值复制到 $A_{01}$中。但因为 $A_{10}^T$ 中的内容是行向量,因此我们需要将 $A_{10}^T$ 进行一次转置:
a01 = (a10t)t; //row
a12t = (a21)t; //col<html>
<img src=“/_media/math/linear_algebra/laff/p_m_q_tr_l_sy.svg” width=“300”>
</html>
上三角矩阵只需要将两者互换即可。
Operations with Matrices
Scaling a Matrix
矩阵的缩放与向量的缩放是一样的。正式定义如下:
Let $L_A : \mathbb R^n \; \rightarrow \; \mathbb R^m$ be a linear transformation and, for all $x \in \mathbb R^n$, define $L_B : \mathbb R^n \; \rightarrow \; \mathbb R^m$ by $L_B(x)=\beta L_A(x)$ where $\beta$ is a scalar.
矩阵缩放的性质
- $A$ 是对称矩阵,那么 $\beta A$ 也是对称矩阵,当 $\beta$ 为标量的时候。
- 第一条性质对三角矩阵,对角矩阵,转置矩阵均适用。
Adding matrices
矩阵的加法与向量相同。正式定义如下:
Let $L_A : \mathbb R^n \rightarrow \mathbb R^m$ and $L_B : \mathbb R^n \rightarrow \mathbb R^m$ both be linear transformations and $$ , for all $x \in \mathbb R^n$ , define the function $L_C: \mathbb R^n \rightarrow \mathbb R^m$ by $L_C(x) =L_A(x)+L_B(x)$ .
算法:矩阵的加法
非常简单的算法。只需要将矩阵进行或者列的分割,再对每一部分对应的分量相加即可。
矩阵加法的性质
- $A + B = B + A$
- $( A + B ) + C = A + ( B + C )$
- $ \gamma (A + B) = \gamma A + \gamma B$, $\gamma$ 为标量
- $ ( \beta + \gamma ) A = \beta A + \gamma A$
- $(A + B)^T = A ^ T + B ^ T$
- 若 $A、B$ 均为对称矩阵,那么 $A+B$ 也为对称矩阵,$\beta A + \gamma B$ 也为对称矩阵,即对称矩阵的任意线性组合也为对称矩阵。
矩阵与向量的乘法:点积解释
参考week2 note 2.1,我们可以得到下面一个等式:
$$
\begin{array}{r c l} A x & = & \left( \begin{array}{c c c c } \chi _{0} \alpha _{0,0} + \chi _{1} \alpha _{0,1} + \cdots + \chi _{n-1} \alpha _{0,n-1} \\ \chi _{0} \alpha _{1,0} + \chi _{1} \alpha _{1,1} + \cdots + \chi _{n-1} \alpha _{1,n-1} \\ \vdots \\ \chi _{0} \alpha _{m-1,0} + \chi _{1} \alpha _{m-1,1} + \cdots + \chi _{n-1} \alpha _{m-1,n-1} \end{array} \right) \\ & = & \left( \begin{array}{c c c c } \alpha _{0,0} & \alpha _{0,1} & \cdots & \alpha _{0,n-1} \\ \alpha _{1,0} & \alpha _{1,1} & \cdots & \alpha _{1,n-1} \\ \vdots & \vdots & & \vdots \\ \alpha _{m-1,0} & \alpha _{m-1,1} & \cdots & \alpha _{m-1,n-1} \\ \end{array} \right) \left( \begin{array}{c} \chi _0 \\ \chi _1 \\ \vdots \\ \chi _{n-1} \\ \end{array} \right) \end{array}
$$
如果我们仔细检查等式第一行的矩阵,我们会发现中间的每一行都是第二行公式中每一行与向量 $x$ 的点积的结果,即:
<html>
<img src=“/_media/math/linear_algebra/laff/m_m_v_dot.svg” width=“500”>
</html>
因此,我们可以从点积的角度归纳出,矩阵与向量 $x$ 的乘法的结果是一个向量 $y$,$y$ 上的每一个分量,等于对应矩阵的行,与向量 $x$ 的点积。因此不难得到点击角度下向量与矩阵乘法的算法:

可以看出的是每次迭代的点积结果,都加到了对应的 $y$ 的分量上。实质上就是一个行优先的循环:
for i = 0, i <= m -1, ++i
for j = 0, j <= n-1, ++j
yi += aij * xj矩阵与向量的乘法:Axpy解释
同样参考week2 note 2.1,如果将矩阵按列分割,那么实际上矩阵与向量的乘积可以通过以下的途径计算:
$$\begin{array}{r c l} A x \\ & =& \left( \begin{array}{c | c | c | c} a_0 & a_1 & \cdots & a_{n-1} \end{array} \right) \left( \begin{array}{c} \chi _0 \\ \chi _1 \\ \vdots \\ \chi _{n-1} \\ \end{array} \right) \\ & =& \chi _0 a_0 + \chi _1 a_1 + \cdots + \chi _{n-1} a_{n-1} \\ & = & \chi _0 \left( \begin{array}{c c c c } \alpha _{0,0} \\ \alpha _{1,0} \\ \vdots \\ \alpha _{m-1,0} \end{array} \right) + \chi _1 \left( \begin{array}{c c c c } \alpha _{0,1} \\ \alpha _{1,1} \\ \vdots \\ \alpha _{m-1,1} \end{array} \right) + \cdots + \chi _{n-1} \left( \begin{array}{c c c c } \alpha _{0,n-1} \\ \alpha _{1,n-1} \\ \vdots \\ \alpha _{m-1,n-1} \end{array} \right) \\ & \end{array}$$
如果我们按列循环,那么每一次循环都可以视作 $x$ 的一个分量与矩阵 $A$ 对应的列的 AXPY 的操作。因此,从AXPY操作来设计矩阵与向量的乘法,我们可以得到如下的算法:

该算法中的每个循环不再进行点积操作,而是进行AXPY操作,但得到的任然是一个向量;通过循环将这个向量累加到 $y$ 上,最终也可以得到矩阵与向量相乘的结果。其实质就是一个列优先的双重循环:
for i = 0, i <= n -1, ++i
for j = 0, j <= m-1, ++j
yi += aij * xj参考资料
- 本页面所有非 svg 图片来源于 LAFF 课件。



