目录

More Gaussian Elimination

LAFF Week 7 Notes

本章的重要内容：

When Gaussian Elimination Works

先来回顾一下 $LU$ 分解中 关于 $Ux = z$ 求解的循环部分，我们发现其中有这么一个过程：
$$\beta_{21} = \beta_{21} / v_{11}$$
这一部分代表了对 multiplier 的计算。如果仔细观察，我们注意到如果 $v_{11}=0$，也就是主对角线元素为 $0$ 的时候，该算法就无法进行下去了。

那么反过来想，如果主对角线所有元素都不为 $0$，那么该算法是有解的。鉴于在 $Lz = b$ 的算法中不包含除法，因此 $Ux=z$ 有解也就意味着整个 $Ax=b$ 有解。那么这里有一个问题：$Ax=b$ 的解是唯一的吗？

我们试着通过反证法来证明一下： 

/* part 1*/
假设：Ax = b 有两个解 u 和 v
那么根据 Ax = b，有
Au = b
Ax = b
因为 A 是 矩阵（线性变换）
因此 A (u - v) = b => Au - Av = b - b = 0
令 u - v = w，即可得 Aw = 0
通过 LU 分解， A = LU
那么 Aw = (LU)w = L(Uw) = 0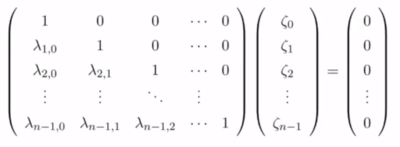
来看一下 $Lz=0$ 意味着什么：

根据上图，我们发现如果要 $Lz = 0$，那么：

  1. $\zeta_0 = 0$
  2. $\lambda_{10}\zeta_0+1*\zeta_1 = 0$

以此类推，我们可以得出 $z$ 必须为 $0$ 的结论。

再来看看通过 $z=0$，也就是 $Uw=0$ 意味着什么：

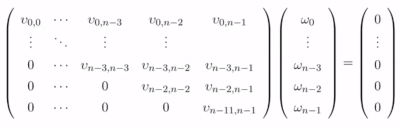
根据之前的假设，我们假设 $Ux=z$ 有解，也就是图中所有的 $v$ 都不为 0，那么有：

  1. $v_{n-1,n-1}w_{n-1} = 0$，因为所有 $v$ 不为 0，那么 $w_{n-1} = 0$
  2. $v_{n-2,n-2}w_{n-2}+v_{n-1,n-1}w_{n-1} = 0$，也就是 $w_{n-2} = 0$

依次类推，可以得出 $w=0$ 的结论，也就是 $u=v$；因此可以推断出只要通 $LU$ 分解求解中，如果主对角线均不为 0 ， $Ax=b$ 必定有且只有一个唯一解。

主对角线有 0 时的问题

当 $U$ 的主对角线上有 0 的时候，麻烦就来了。根据 $Ux=z$ 的算法，我们不可避免的遭遇到除 0 的情况。该情况会导致算法无法继续进行；但问题在于，有时算法的无法进行并不代表我们无法得出解。下面是一个很明显的例子：

$$ \displaystyle \left( \begin{array}{c c} 0 & 1 \\ 1 & 0 \end{array} \right) \left( \begin{array}{c} x_0\\ x_1 \end{array} \right) = \left( \begin{array}{c} \beta_0\\ \beta_1 \end{array} \right) $$
上式很显然有解，但我们并不能通过之前学习的算法来求解。因此，我们需要引进置换矩阵的概念来解决这个问题。

置换矩阵 Permutations Matrix

置换矩阵（Permutations Matrix）可以简要的概述为每行每列有且只有一个 1，其他元素都为 0 的方阵；比如下图的矩阵就是一个置换矩阵：

$$\left(\begin{array}{c}0&1&0\\0&0&1\\1&0&0\end{array}\right)$$

置换这个名字非常形象。以上面的置换矩阵为例，来看一个矩阵的乘法：

$$ \left(\begin{array}{c}0&1&0\\0&0&1\\1&0&0\end{array}\right) \left(\begin{array}{c}-2&1&2\\3&2&1\\-1&0&-3\end{array}\right) = \left(\begin{array}{c}3&2&1\\-1&0&-3\\-2&1&2\end{array}\right) $$

这个例子有趣的地方在于，如果将置换矩阵改为单位矩阵 $I$，再对两个乘法进行对比，我们会发现其实置换矩阵改变的是目标矩阵行的排序，而该排序正好对应置换矩阵中行之余单位矩阵中的行的位置：

<html>

<img src=“/_media/math/linear_algebra/laff/premult_mat.svg” width=“450”>

</html>

置换矩阵的一般形式

大致知道置换矩阵的功能之后，我们来考虑一下置换矩阵的一般形式。我们注意到，无论是从行还是列来看待置换矩阵，置换矩阵都可以看作是一个由 Unit basis vector 组成的向量。如果我们使用向量 $p$ 代表置换矩阵中 Unit basis vector 的顺序，那么 $p$ 可以表示为：

$$ p = \left( \begin{array}{c} k_0, \cdots, k_{n-1} \end{array} \right)^T $$

现在使用 $P$ 来表示对应 $p$ 的置换矩阵，那么有：

$$ P(p) = \left( \begin{array}{c} \widetilde e_{k_0}^T \\ \hline \widetilde e_{k_1}^T \\ \hline \vdots \\ \hline \widetilde e_{k_{n-1}}^T \end{array} \right) $$

假设我们的目的是用 $P$ 对 $A$ 中的行为单位排序，那么我们需要将 $P$ 和 $A$ 都按照行来划分，因此有： $$ PA = P(p)A = \left( \begin{array}{c} \widetilde e_{k_0}^T \\ \hline \widetilde e_{k_1}^T \\ \hline \vdots \\ \hline \widetilde e_{k_{n-1}}^T \end{array} \right) \left( \begin{array}{c} \widetilde a_0^T \\ \hline \widetilde a_1^T \\ \hline \vdots \\ \hline \widetilde a_{n-1}^T \end{array} \right) = \left( \begin{array}{c} \widetilde a_{k_0}^T \\ \hline \widetilde a_{k_1}^T \\ \hline \vdots \\ \hline \widetilde a_{k_{n-1}}^T \end{array} \right) $$

注意这里 $e^T_iA$ 代表的就是 $A$ 的第 $i$ 行。



而如果需要对 $A$ 按列为单位排序，为了得到与 $A$ 维度相同的矩阵，我们需要使用 $P^T$ 对 $A$ 进行右乘：

$$ AP^T = A \left( \begin{array}{c} \widetilde e_{k_0}^T \\ \hline \widetilde e_{k_1}^T \\ \hline \vdots \\ \hline \widetilde e_{k_{n-1}}^T \end{array} \right)^T =A\left( \begin{array}{c|c|c|c} e_{k_0} & e_{k_1} & \dots & e_{k_{n-1}} \end{array} \right)\\ =\left( \begin{array}{c|c|c|c} Ae_{k_0} &A e_{k_1} & \dots & Ae_{k_{n-1}} \end{array} \right) =\left( \begin{array}{c|c|c|c} a_{k_0} & a_{k_1} & \dots & a_{k_{n-1}} \end{array} \right) $$

使用转置矩阵解决除零问题

通过上面对转置矩阵的了解，我们知道可以通过转置矩阵控制目标矩阵中行（列）的位置。这一点对于解决高斯变换（LU 分解）中除零的问题是非常有效的。对于对角线中元素是 0 的情况，我们的处理思路就是将这一行与其他的行进行交换；这样的交换有可能使高斯变换避免计算中除零的情况。

理想中对目标矩阵行的交换只牵涉到两行，因此我们需要引进一种更加具体的置换矩阵 $\tilde P( \pi )$，我们称之为 Pivot Matrix（中文： 枢轴矩阵，翻译可能不准确）。在 $\tilde P( \pi )$ 中，只有第 $\pi$ 行与第一行发生了交换，其他行都保持不变。具体的演示如下图：



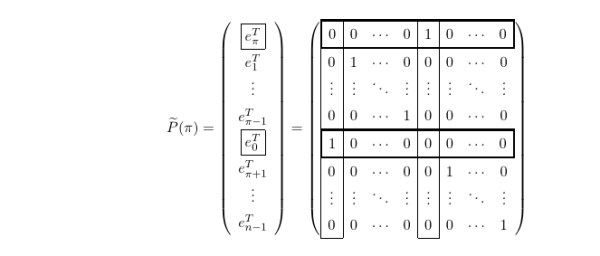
可以注意到的是：

算法：LU Factorization with Partial Pivoting

该算法基本上高斯变换的算法相同，只需要添加一个条件分支即可：

<html>

<img src=“/_media/math/linear_algebra/laff/pivot_al.svg” width=“250”>

</html>

总的说来，本算法分两个大步骤。第一个步骤是对目标矩阵进行 LU 分解，并求出 $p$。该过程手动计算的过程大致如下：

  1. 每一个循环都需要应用和更新代表高斯变换的矩阵（$L$）。
  2. 查看目标对角线上的当前循环的元素，如果不为 0，无需交换行。也就是说使用 $I$ 作为置换矩阵；并将 $p$ 中对应的分量设置为 0（$p$ 对应分量负责存储 $\pi$ 的值，0 代表当前没有置换的行）
  3. 如果当前循环对角线上元素为 0，查看当前行下方，选取当前行正下方元素不为 0 的第一行进行交换（应用对应的置换矩阵），并记录下用于交换行的行数到 $p$ 对应的分量中。
  4. 如此反复，直到完成 $LU$ 分解。

当完成这部分计算以后，第二个步骤是使用 $p$ 来对 $b$ 进行更新。简单的说来，因为换过行，因此不但 $A$ 中的行要随之变化，对应的 $b$ 中的分量也要随之变化。（这个很好理解：某一个方程等式左边和右边应该视作一个整体一起交换）。也就是说， 

因为 Ax = b
所以 PAx = Pb //保持相等

整个完整的算法如下图所示：



跟之前的 LU 分解相比，上图唯一的变化就是先求出 $p$，然后使用 $p$ 更新 $b$。接着就是我们熟悉的两步： $Lz=b$ 与 $Ux = z$ 了。

当然，我们还会遇到一种情况：矩阵中根本就找不到合适的一行与当前含 0 行进行替换。这象征着 $Ax=b$ 无解或者有无限多解，该内容将在第八章中详述。

Inverse Matrix

在高中我们都学过反函数。反函数可以理解为一个映射的逆映射，也就是还原当前映射。令原函数为 $f$，反函数为 $f^{-1}$，则下方数学表达式表达了如下关系：
$$ f^{-1}(f(x)) = x $$
很显然，原函数中的自变量和因变量必须要一一对应，才能完成这样的“还原”。

下面再来看看矩阵。根据之前的知识，我们知道矩阵也是映射的一种。与反函数相似，如果存在这么一个矩阵，可以还原某个矩阵表示的映射，那么我们就称这个矩阵是原矩阵的逆矩阵。而原矩阵，我们也称为非奇异矩阵（Nonsingular Matrix）。

当然，相较于 1D 函数，矩阵是向量的函数，映射前与映射后维度可能发生变化 $f: \mathbb{R}^n \to \mathbb{R}^m)$。但因为逆矩阵必须要求映射的定义域与值域有着一一对应的关系，那么只有当 $m=n$，也就是原矩阵是方阵的时候，才有可能存在逆矩阵。

逆矩阵的基本性质

  1. 逆矩阵也是线性变换
  2. $AA^{-1} = I$
  3. $(aB)^{-1} = \frac{1}{a}B^{-1} $
  4. $(AB)^{-1} = B^{-1}A^{-1}$
  5. $(ABC)^{-1} = C^{-1}B^{-1}A^{-1}$
  6. $(A^T)^{-1} = (A^{-1})^T$

特殊矩阵的逆矩阵

详情如下图：



当然，不管是什么矩阵，求其逆矩阵的主要方法都是通过 $AA^{-1} = I$ 这个关系来求。进一步的说，我们可以将 $I$ 按列划分，按列得出关系，一列一列的求逆矩阵。（例子待添加）FIXME

参考资料