目录
More on Matrix Inversion
LAFF Week 8 Notes
本章的重点:
- Guass-Jordan 方法求解 $Ax = b$、算法和消耗
- Guass-Jordan 方法求解逆矩阵
When Row Pivoting Fails
之前我们了解到使用置换矩阵可以对高斯变换中 a11 为 0 的情况进行处理:将 a01 下方元素不为 0 的第一行与 a01 所在的行交换即可解决问题。不过这里有一种更麻烦的情况:如果 a01 下方的元素全为 0 呢?
很显然这种情况下,高斯变换是没有办法进行下去的。那么高斯变换无法进行下去到底意味着什么呢?
可以想到,高斯变换实际上就是对矩阵所代表的方程组求解的一种方式。因此可以推测,高斯变换的无法进行应该代表该方程组是无解的。而联想到方程组有唯一解等价于代表方程组映射的矩阵存在逆矩阵,我们可以假设:某行 a01 下方全为 0 的矩阵,没有逆矩阵,也就是说,该矩阵是奇异矩阵(Singular Matrix)。只要说明该矩阵是奇异矩阵,就可以证明高斯变换无法进行代表该方程组无解。
为了验证这个假设,我们先引入一个推论:
假设 $C =BA$,$B$ 为非奇异矩阵。那么 $C$ 为非奇异矩阵的充要条件是 $A$ 为非奇异矩阵。
这个推论很好证明:
假设上面推论成立:
则:C^-1 = A^-1 B^-1
那么 C^ * C^-1 = B * A * A^-1 * B^-1 = B * I * B^-1 = BB^-1 = I
根据矩阵与其自身逆矩阵乘积为 I 的性质,该推论得证。a01 下面都是 0 的矩阵长什么样子:
$$ \left( \begin{array}{r | r r} A_{00} & a_{01} & A_{02} \\ \hline 0 & 0 & a^T_{12}\\ 0 & 0 & A_{22} \end{array} \right) $$
注:此时高斯变换开始通过 $a_{01}$ 下方的元素求
multiplier
为了说明上述的矩阵是奇异矩阵,我们需要引入之前证明过的第二个推论:
若 $A$ 为非奇异矩阵,那么如果 $Ax = 0$,则有 $x = 0$。
对上述的矩阵,我们构造一个非零 $x$ 如下:
$$
\left( \begin{array}{r | r r}
A_{00} & a_{01} & A_{02} \\
\hline
0 & 0 & a^T_{12}\\
0 & 0 & A_{22}
\end{array} \right)
\begin{pmatrix}
-A_{00}^{-1}a_{01} \\
\hline
1 \\
\hline
0
\end{pmatrix}
$$
上述的运算得到的结果实际上是一个 3*1 的零向量。那么我们有如下推论:
假设 A 为非奇异矩阵, Ax = 0 => x = 0;
因为 x ≠ 0 且 Ax = 0;
可知 A 为奇异矩阵。a11 不为零,是 $A$ 为非奇异矩阵的充要条件。进一步说,$A$ 是非奇异矩阵(有唯一解)的充要条件是 LU 分解会最终生成一个对角线元素不含零的上三角矩阵(无论通不通过置换行)。
Gauss-Jordan elimination
高斯消元法还有一种变种,称为高斯-约当消元法(Gauss-Jordan elimination)。这种方法和高斯消元法最主要的区别是,高斯-约当消元法会依次选取每个未知数所对应的对角线元素所在行作为主元(pivot),以此为基础进行消元;而高斯消元法则拥有确定的、不会更改的主元。
下面是一个具体的高斯-约当消元法例子:
第一步中,第一个未知数 $\chi_0$ 对角元素为 2,处于第一行,因此以 2 所在行列式作为主元进行消元:
$$
\begin{array}{r r r r} \hline \color{red}{-2 \chi_0} + & 2 \chi_1 - & 5 \chi_2 = & -7 \\ \hline 2 \chi_0 + & -3 \chi_1 + & 7 \chi_2 = & 11 \\ -4 \chi_0 + & 3 \chi_1 - & 7 \chi_2 = & -9 \end{array} \rightarrow \begin{array}{r r r r} \hline -2 \chi_0 + & 2 \chi_1 - & 5 \chi_2 = & -7 \\ \hline & - \chi_1 + & 2 \chi_2 = & 4 \\ & - \chi_1 + & 3 \chi_2 = & 5 \end{array}
$$
经过第一步的消元以后,我们得到了一个新的方程组。新的方程组中 第二个未知数 $\chi_1$ 在对角线上的元素为 -1,处于第二行,因此以 -1 所在行作为主元进行消元:
$$
\begin{array}{r r r r} -2 \chi_0 + & 2 \chi_1 - & 5 \chi_2 = & -7 \\ \hline & \color{red}{ - \chi_1} + & 2 \chi_2 = & 4 \\ \hline & - \chi_1 + & 3 \chi_2 = & 5 \end{array} \rightarrow \begin{array}{r r r r} -2 \chi_0 + & & - \chi_2 = & 1 \\ \hline & - \chi_1 + & 2 \chi_2 = & 4 \\ \hline & & \chi_2 = & 1 \end{array}
$$
之后方程组再次更新。我们接着寻找 $\chi_2$ 在对角线上的元素,发现处于第三行,因此以第三行作为主元进行消元:
$$
\begin{array}{r r r r} -2 \chi_0 + & & - \chi_2 = & 1 \\ & - \chi_1 + & 2 \chi_2 = & 4 \\ \hline & & \color{red}{\chi_2} = & 1 \\ \hline \end{array} \rightarrow \begin{array}{r r r r} -2 \chi_0 & & = & 2 \\ & - \chi_1 + & = & 2 \\ \hline & & \chi_2 = & 1 \\ \hline \end{array}
$$
到此此事后,我们发现所求的 $\chi$ 中的各个分量都对应了单独的标量,因此我们只需要让他们的系数归一即可:
$$
\begin{array}{r r r r} -2 \chi_0 & & = & 2 \\ & - \chi_1 + & = & 2 \\ \hline & & \chi_2 = & 1 \\ \hline \end{array} \rightarrow \begin{array}{r r r r} \chi_0 & & = & -1 \\ & \chi_1 + & = & -2 \\ \hline & & \chi_2 = & 1 \\ \hline \end{array}
$$
上面就是高斯-约当消元法的完整过程。
使用高斯-约当方法求解Ax=b
现在我们将上面的式子写成矩阵的形式。跟高斯消元法相同,我们做如下两步处理:
- 将方程组写成 Append Matrix 的形式
- 使用单位矩阵存储消元的过程
根据上面的处理,之前例子中的方程组求解可以写成如下形式:
$$
\left( \begin{array}{|r|r r} \hline 1 & 0 & 0 \\ \hline 1 & 1 & 0 \\ -2 & 0 & 1 \end{array} \right) \left( \begin{array}{|r|r r|r|r} \hline \color{red}{-2} & 2 & -5 & & -7 \\ \hline 2 & -3 & 7 & & 11 \\ -4 & 3 & -7 & & -9 \end{array} \right) =
\left( \begin{array}{|r r r | r} \hline -2 & 2 & -5 & -7\\ \hline 0 & -1 & 2 & 4 \\ -0 & -1 & 3 & 5 \end{array} \right) \tag{step.1}
$$
$$
\left( \begin{array}{r|r|r} 1 & 2 & 0 \\ \hline 0 & 1 & 0 \\ \hline 0 & -1 & 1 \end{array} \right) \left( \begin{array}{r|r| r|r|r} -2 & 2 & -5 & & -7 \\ \hline 0 & \color{red}{ -1} & 2 & & 4 \\ \hline 0 & -1 & 3 & & 5 \end{array} \right) =
\left( \begin{array}{r r r | r} -2 & 2 & -5 & -7\\ 0 & -1 & 2 & 4 \\\hline 0 & -1 & 3 & 5 \end{array} \right)
\tag{step.2}
$$
$$
\left( \begin{array}{r r|r|} 1 & 0 & 1 \\ 0 & 1 & -2 \\ \hline 0 & 0 & 1 \\ \hline \end{array} \right) \left( \begin{array}{|r r|r|r|r|r} -2 & 0 & -1 & & & 1 \\ 0 & -1 & 2 & & & 4 \\ \hline 0 & 0 & \color{red}{1} & & & 1 \\ \hline \end{array} \right) =
\left( \begin{array}{r r r | r} -2 & 0 & 0 & 2\\ 0 & -1 & 0 & 2 \\ \hline 0 & 0 & 1 & 1 \\\hline \end{array} \right)
\tag{step.3}
$$
$$
\left( \begin{array}{r r r} -1/2 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{r r r|r|r} -2 & 0 & 0 & & 2 \\ 0 & -1 & 0 & & 2 \\ 0 & 0 & 1 & & 1 \end{array} \right) =
\left( \begin{array}{r r r|r|r} -1 & 0 & 0 & & -1 \\ 0 & 1 & 0 & & -2 \\ 0 & 0 & 1 & & 1 \end{array} \right)
\tag{step.4}
$$
高斯-约当算法
将上面的过程写成算法的一般形式,有:
$$
\left( \begin{array}{r|r|r} I & -u_{01} & 0 \\ \hline 0 & 1 & 0 \\ \hline 0 & -l_{21} & I \end{array} \right) \left( \begin{array}{r|r|r|r|r} D_{00} & a_{01} & A_{02} & & b_0 \\ \hline 0 & \alpha_{11} & a^T_{12} & & \beta_1 \\ \hline 0 & a_{21} & A_{22} & & b_2 \end{array} \right)
\tag{Nor.1}
$$
我们发现实际上每一次消元都处于对角线元素的上方和下方。因此,我们可以根据对角线元素上方和下方的内容求得 multiplier,即:
u01 = a01 / a11 //对角线上方
l21 = a21/ a11 //对角线下方$$ \left( \begin{array}{r|r|r|r|r} D_{00} & 0 & A_{02} - u_{01} a^T_{12} & & b_0 - \beta_{1}u_{01} \\ \hline 0 & \alpha_{11} & a^T_{12} & & \beta_1 ~~~~~\\ \hline 0 & 0 & A_{22} - l_{21}a^T_{12} & & b_2 - \beta_1 l_{21} \end{array} \right) $$
按照顺序来看看这个循环中的运算:
/*Tier.1 Multiplier*/
u01 = a01 / a11
l21 = a21/ a11
/*Tier.2 elimination & update matrix by rank 1*/
A02 = A02 - u01 * a12t
A22 = A22 - l21 * a12t
/*Tier.3 update appendix*/
b0 = b0 - a01 * beta1 //更新方式是点乘,单次更新一个标量
b2 = b2 - a21 * beta1 //注意位置
/*Tier.4 [important] 用零表示已经消元的元素 */
a01 = 0
a21 = 0multiplier 存储在代表方程组的矩阵中,这里我们也可以做同样的操作:
/*replace all u01 by a01, all l21 by a21*/
/*Tier.1 Multiplier*/
a01 = a01 / a11
a21 = a21/ a11
/*Tier.2 elimination & update matrix by rank 1*/
A02 = A02 - a01 * a12t
A22 = A22 - a21 * a12t
/*Tier.3 update appendix*/
b0 = b0 - a01 * beta1
b2 = b2 - a21 * beta1
/*Tier.4 [important] 用零表示已经消元的元素 */
a01 = 0
a21 = 0a11 归 1 的操作。当前 $b$ 向量中的分量 值为 $\beta_1$,a11 更新后,我们也要对其进行更新:
beta1 = beta1 / a11
a11 = 1高斯-约当算法:求多组解
高斯-约当消元求出的结果是一个关于未知数的向量(解)。基于不同的 $b$,我们得到的解也不同,但运算的过程是相同的。因此,我们有必要找出一种可以重复利用当前方程组运算过程(也就是 append matrix 左边)的方法。
我们注意到之前的算法中,对代表解的向量 $\beta$ 的更新是通过存储 multiplier 的矩阵来实现的。回想一下矩阵与矩阵的乘法,如果按照列更新的观点来看待的话,那么矩阵与矩阵的乘法可以看作是多个矩阵与列向量的乘法。因此,我们可以将运算矩阵 $A$ 一次性的应用到不同的 $b$ 上;也就是说,将不同的 $b$ 组成一个矩阵,而求出的 $x$ 也是一个矩阵;两个矩阵之间按列对应结果。 按照之前的例子,如果我们有另外一组 $b$:
$$
\begin{pmatrix}
8 \\
\hline
-13 \\
\hline
9
\end{pmatrix}
$$
那么之前的整个高斯-约当的求解矩阵就可以写为:
$$
\left( \begin{array}{rrr|r|r r} -2 & 2 & -5 & & -7 & 8 \\ 2 & -3 & 7 & & 11 & -13 \\ -4 & 3 & -7 & & -9 & 9 \end{array} \right)
$$
也就是说,我们通过将 $x$ 和 $b$ 表示为矩阵实现了对多组不同的 $b$ 同时求解对应 $x$ 的方法。如果用 $B$ 表示 $b$ 组成的矩阵,那么高斯-约当方法就可以表示成如下的乘法:
$$
\left( \begin{array}{r|r|r} I & -u_{01} & 0 \\ \hline 0 & 1 & 0 \\ \hline 0 & -l_{21} & I \end{array} \right) \left( \begin{array}{r|r|r|r|r} D_{00} & a_{01} & A_{02} & & B_0 \\ \hline 0 & \alpha_{11} & a^T_{12} & & b_{1}^T \\ \hline 0 & a_{21} & A_{22} & & B_2 \end{array} \right)
$$
得到的结果为:
$$
\left( \begin{array}{r|r|r|r|r} D_{00} & a_{01} - \alpha_{11}u_{01} & A_{02} - u_{01} a^T_{12} & & B_0 - u_{01}b_{1}^T \\ \hline 0 & \alpha_{11}~~~~~ & a^T_{12} & & b_{1}^T \\ \hline 0 & a_{21} - \alpha_{11} l_{21} & A_{22} - l_{21}a^T_{12} & & B_2 - l_{21} b_{1}^T \end{array} \right)
$$
而如果我们将对角线元素的计算
u01 = a01 / a11
l21 = a21/ a11$$ \left( \begin{array}{r|r|r|r|r} D_{00} & 0 & A_{02} - u_{01} a^T_{12} & & B_0 - u_{01}b_{1}^T \\ \hline 0 & \alpha_{11} & a^T_{12} & & b_{1}^T \\ \hline 0 & 0 & A_{22} - l_{21}a^T_{12} & & B_2 - l_{21} b_{1}^T \end{array} \right) $$
很显然,与之前求单组解的高斯-约当方法相比,这里唯一的改变就是对向量 $\beta$ 的更新变成了对 矩阵 $B$ 的更新。因此我们只需要修改算法的局部就可以了:
/*Tier.1 Multiplier*/
u01 = a01 / a11
l21 = a21/ a11
/*Tier.2 elimination & update matrix by rank 1*/
A02 = A02 - u01 * a12t
A22 = A22 - l21 * a12t
/*Tier.3 update appendix*/
B0 = B0 - a01 * b1t //注意这里是 rank1 更新
B2 = B2 - a21 * b1t //注意位置
/*Tier.4 [important] 用零表示已经消元的元素 */
a01 = 0
a21 = 0b1t = (1 / a11) * b1t
a11 = 1高斯-约当方法求逆矩阵
如果仔细观察上面的运算过程,我们实际上完成了一种运算的转换:
$$ Ax = b \,\,\, \to \,\,\, AX = B$$
也就是把高斯-约当方法从矩阵与向量之间扩展到了矩阵与矩阵之间。而我们来考虑一下下面的方程:
$$AX = I$$
眼尖的同学可能已经发现,这里的 $X$ 就是 $A$ 的逆矩阵。而我们完全可以将高斯-约当消元法套用到求逆矩阵的过程中。实际上,通过列观点看上式,实际上就是在求一组如下的方程:
$$
A(x_0|x_1| \cdots \ x_{n-1}) = (e_0|e_1|\cdots|e_{n-1})
$$
也就是
$$
Ax_j = e_j
$$
明白了原理之后,我们按照普通的高斯-约当方法,将整个运算过程按照下面的格式排列出来:
<html>
<img src=“/_media/math/linear_algebra/laff/gauss-jordan_1-2.svg” class = “mediacenter” width=“600”>
</html> 整个笔算的大致流程如下:
- L 对 U 进行更新,得到的结果存储在 U' 中。
- L 对 I 进行更新,得到的结果存储在 X' 中。
- 将 U' 作为新一轮的 U, X' 作为新一轮的 I,接着使用下一轮的 L 进行更新。
- 重复上述步骤直到 LU 分解完成。
- 最后将 U 中的对角线系数归 1,并将归 1 矩阵应用到 X' 上。
有几点需要解释:
- 上面的过程只代表了笔算的过程,并不是算法的过程。
- 这里的 $L$ 只存储每次消元的
multiplier。 - U 中的初始内容是 A,只是通过 LU 分解 A 会最终变成 U, 因而称那一部分为 “U”。
实际上这里就是一个已知 $A,I$ 通过 $AX = I$ 用高斯-约当消元求 $X$ 的过程。
高斯-约当求逆算法的实现
相较于笔算直接将 L 应用到整个 X' 上,计算机上的高斯-约当算法在处理 X' 的更新上,是将其与 B 放置在一块的。我们以一个例子来看看整个更新的过程。
假设我们有如下矩阵。根据高斯-约当的消元步骤,我们可以得出第一步所需的 $L_0$ :
<html>
<img src=“/_media/math/linear_algebra/laff/g-j-al-1.svg” width=“400”>
</html>
通过计算我们可以得到如下矩阵:
<html>
<img src=“/_media/math/linear_algebra/laff/g-j-al-2a.svg” width=“600”>
</html>
此时发生了两个更新:
- $L_0$ 与 $U_0$ 的更新 得到 $U'_1$
- $L_0$ 与 $I_0$ 的更新 得到 $X'_1$
注意此时的 $X'$,$X'_0$ 的初始状态是一个 3*3 的单位矩阵,通过当前循环 $L_0$ 的更新为图示的矩阵 $X'_1$。
接下来我们以当前的 $U'_1$ 和 $X'_1$ 作为新一轮的初始值,接着计算下一轮的 $U'_2$ 和 $X'_2$:
<html>
<img src=“/_media/math/linear_algebra/laff/g-j-al-3a.svg” width=“600”>
</html>
本算法的 trick 基本上就蕴含在这一步的形式中。注意观察上面的图像:
- 由于 $L$ 是按列进行消元操作的,因此 $L$ 的更新只会影响到对应的列,也就是对指定的未知数系数进行消元。
- 因此我们将 $U、I$ 视作一个整体(本身来说就是一个整体)进行更新,而我们只需要找出 $L$ 每个循环中对应的更新部分就可以了。
- 在本步骤中,$L_1$ 通过第二列对 $U'_1、I_1$更新,而我们注意到,$U'_1$ 中的灰色部分是已经消元的部分,不用再更改,因此对应 $L_1$ 中的灰色部分。
- 而 $I_1$中的浅黄色部分通过 $L_1$ 中的更新,直接等于将 $L_1$ 更新的部分复制到了 $X'_2$ 的绿色区域中。
通过上述的观察,我们就能大致明白该算法里发生了什么了:
- 更新操作一:对 $U'$ 中没有完成消元的部分加上 $X'$(当前 I) 之前更新过的部分进行更新。
- 更新操作二:使用 L 对 X(当前 I)还是 $e$ 的内容(上图浅黄色区域)进行对应列的更新。这样的更新等于直接将当前 L 中的更新列复制到 X 的对应列中,操作十分方便。
接下来是第三轮,依然是同样的策略:
<html>
<img src=“/_media/math/linear_algebra/laff/g-j-al-4.svg” width=“600”>
</html>
到此我们已经完成了 LU 分解。 此时只需要将 $U'$ 中的对角线归 1,我们就能得到最后要求的 $X$, 也就是 $A^{-1}$ 了:
<html>
<img src=“/_media/math/linear_algebra/laff/g-j-al-5a.svg” width=“600”>
</html>
根据上面的推导,我们将该算法的一般形式归纳如下。注意看这里的 L 只包含当前变量消元的 multiplier。
$$
\left( \begin{array}{ c | c | c } I & -u_{01} & 0 \\ \hline 0 & 1 & 0 \\ \hline 0 & -l_{21} & I \end{array} \right) \left( \begin{array}{ c | c | c |c | c | c | c } D_{00} & a_{01} & A_{02} & & B_{00} & 0 & 0 \\ \hline 0 & \alpha _{11} & a_{12}^ T & & b_{10}^ T & 1 & 0 \\ \hline 0 & a_{21} & A_{22} & & B_{20} & 0 & I \end{array} \right)
$$
相乘可以得到结果:
$$
\left( \begin{array}{ c | c | c || c | c | c | c } D_{00} & a_{01} - \alpha _{11} u_{01} & A_{02} - u_{01} a_{12}^ T & & B_{00} - u_{01} b_{10}^ T & - u_{01} & 0 \\ \hline 0 & \alpha _{11} & a_{12}^ T & & b_{10}^ T & 1 & 0 \\ \hline 0 & a_{21}- \alpha _{11} l_{21} & A_{22} - l_{21} a_{12}^ T & & B_{20} - l_{21} b_{10}^ T & - l_{21} & I \end{array} \right)
$$
代入:
u01 = a01 / a11
l21 = a21/ a11$$ \left( \begin{array}{ c | c | r | c | r | c | c } D_{00} & 0 & A_{02} - u_{01} a_{12}^ T & & B_{00} - u_{01} b_{10}^ T & - u_{01} & 0 \\ \hline 0 & \alpha _{11} & a_{12}^ T & & b_{10}^ T & 1 & 0 \\ \hline 0 & 0 & A_{22} - l_{21} a_{12}^ T & & B_{20} - l_{21} b_{10}^ T & - l_{21} & I \end{array} \right) $$
那么算法实际上就很清晰了:

这里还有个小差别,上述算法的实现中将结果部分整个看成了一个大矩阵 B,因此对 L 对 X' 的更新对应的是 $b_{01}$ 和 $b_{21}$。在这列的左边是 U 的内容,在这列右边的是还未更新的内容。
大致的实现步骤同样分两步,实现如下:
/*Part A: update with LU decomp*/
/*replace all u01 by a01, all l21 by a21*/
/*Tier.1 Multiplier*/
a01 = a01 / a11
a21 = a21 / a11
/*Tier.2 elimination & update matrix by rank 1*/
A02 = A02 - a01 * a12t
A22 = A22 - a21 * a12t
/*Tier.3 update appendix*/
B00 = B00 - a01 * b10t // rank 1 update for U and a part of X
B20 = B20 - a21 * b10t
/*Tier.4 copy current col of L to corresponding col of X */
b01 = -a01
b21 = -a21
/*Tier.5 [important] 用零表示已经消元的元素 */
a01 = 0
a21 = 0
/*Part B, update daig element to 1*/
b10t = b10t / a11 //
beta11 = beta11 / a11
b12t = b12t / a11
a11 =1高斯-约当算法求逆的改进
到目前为止,我们的算法都是分成两部分的:一部分完成 LU 分解,另外一部分使对角线元素归一。实际上,我们可以对 $L$ 进行一些改进:在消元的同时完成对当前对角线元素的归一,这样一来就可以更加效率了。
方法也非常简单。每一轮我们都会进行消元,而主元上位于对角线上的元素是一定存在的。因此只需要在 L 中乘上与之对应的倒数即可。比如下面的式子:
$$
\left( \begin{array}{r|r r} 1 & 0 & 0 \\ \hline 1 & 1 & 0 \\ -2 & 0 & 1 \end{array} \right) \left( \begin{array}{r|r r|r|r} \color{red}{-2} & 2 & -5 & & -7 \\ \hline 2 & -3 & 7 & & 11 \\ -4 & 3 & -7 & & -9 \end{array} \right)
$$
消元后主元在主对角线上的元素为 $-2$,因此修改其中的 L 中对应元素为 $-\frac{1}{2}$ 为如下:
$$
\left( \begin{array}{r|r r} \color{red}{-1/2} & 0 & 0 \\ \hline 1 & 1 & 0 \\ -2 & 0 & 1 \end{array} \right) \left( \begin{array}{r|r r|r|r} \color{red}{-2} & 2 & -5 & & -7 \\ \hline 2 & -3 & 7 & & 11 \\ -4 & 3 & -7 & & -9 \end{array} \right)
$$
其一般形式就是通过在 L 中添加 $\delta11$对对角线元素 a11 进行归一:
$$
\left( \begin{array}{ c | c | c } I & -u_{01} & 0 \\ \hline 0 & \delta_{11} & 0 \\ \hline 0 & -l_{21} & I \end{array} \right) \left( \begin{array}{ c | c | c |c | c | c | c } I & a_{01} & A_{02} & & B_{00} & 0 & 0 \\ \hline 0 & \alpha _{11} & a_{12}^ T & & b_{10}^ T & 1 & 0 \\ \hline 0 & a_{21} & A_{22} & & B_{20} & 0 & I \end{array} \right)
$$
根据下面的关系对其进行化简:
u01 = a01 / a11
l21 = a21 / a11
delta11 = 1 / a11$$ \left( \begin{array}{ c | c | c } I & -u_{01} & 0 \\ \hline 0 & \delta_{11} & 0 \\ \hline 0 & -l_{21} & I \end{array} \right) \left( \begin{array}{ c | c | c |c | c | c | c } I & a_{01} & A_{02} & & B_{00} & 0 & 0 \\ \hline 0 & \alpha _{11} & a_{12}^ T & & b_{10}^ T & 1 & 0 \\ \hline 0 & a_{21} & A_{22} & & B_{20} & 0 & I \end{array} \right) $$
整个算法的循环部分可以写为:
/*Part A: update with LU decomp*/
/*replace all u01 by a01, all l21 by a21*/
/*Tier.1 Multiplier*/
a01 = a01 / a11
a21 = a21 / a11
/*Tier.2 elimination & update matrix by rank 1*/
A02 = A02 - a01 * a12t
A22 = A22 - a21 * a12t
/*Tier.3 update appendix*/
B00 = B00 - a01 * b10t // rank 1 update for U and a part of X
B20 = B20 - a21 * b10t
/*Tier.4 copy current col of L to corresponding col of X */
b01 = -a01
b21 = -a21
/*Tier.5 [important] 用零表示已经消元的元素 */
a01 = 0
a21 = 0
/*Tier.6 update a12t & b10t & beta11*/
a12t = a12t / a11
b10t = b10t / a11
beta11 = 1 / a11
/*Tier.7 set diag to 1*/
a11 = 1使用 A 存储 B
在每次循环中,我们都是用 L 和 A 计算出 B,然后剩余的结果作为下一轮的 A 继续计算。因此,我们可以将所有的运算直接累加到 A 上,这样就不用使用另外一块空间来存储 B 了。
算法的实现部分是需要将之前算法中所有 B 的部分改成对应的 A 的部分即可。而这样做还带来另外一个好处,不用再对 a01 和 a21 置零,也不用对 a11 置一了。
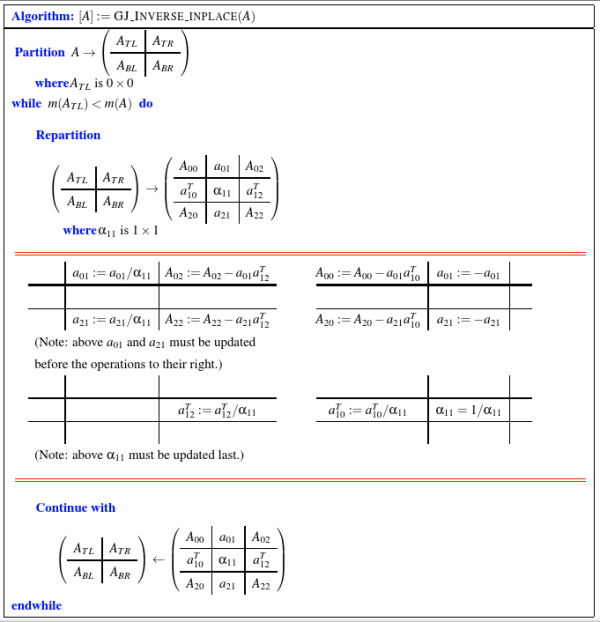
高斯-约当方法也会遇到对角线元素为 0 或对角线以及其下方所有元素为 0 的情况。按照高斯消元的处理即可。
高斯-约当求逆矩阵的消耗
高斯-约当算法的实质是在求一系列的 $Ax_j = e_j$。该算法同时也适用了 LU 分解,因此我们可以将该算法分成如下几个部分:
for j = 0, j < n, ++j
Factor A = LU // 2/3 n^3 flops
Slove Lz = ej n^2 flops
Slove Uxj = z n^2 flops不过我们可以优化一下:LU 分解针对的是同一个矩阵,因此我们可以先分解完该矩阵再解,也就是把 LU 分解剔除出循环外。那么修改后的消耗为 $\frac{2}{3}n^3 +(n^2 + n^2)n = \frac{8}{3}n^3$。
第二个方法是将 A 和 B 两个矩阵放在一起处理。因为我们发现算法中变量矩阵的过程是相同的。与此同时,算法中的主要消耗部分也是在进行 rank1 update 的时候。放在一起的消耗如下图:

比之前的 $ \frac{8}{3}n^3$ 又进了一步。
不要使用求逆的方法求解 Ax=b
如果通过上述求逆的方法来求 x,代价会非常高:
- 求逆的消耗是 $2n^3$
- 解 $b= A^{-1}x$ 的消耗是 $2n^3$
- 总消耗比之前使用 LU 分解来求高出太多
两种特殊情况下可以使用该方法求解:
- 求逆矩阵的时候
- 求SPD矩阵的逆矩阵的时候
SPD矩阵

参考资料
- 本章所有非 svg 图片来源于 LAFF