目录
Vector Spaces
LAFF Week 9 Notes
本章重点大致有两点:
- 通过高斯-约当方法的结果判定解的数量
- 集合、向量空间的相关概念
从多项式到方程解
先来看看下面的例子:
假设知道二次函数上三点:$(-2,-1),(0,2),(2,3)$,求该二次函数的具体表达式。
按照中学的解法,二次多项式表示为 $p(x) = \gamma_0 + \gamma_1\chi +\gamma_2 \chi^2$。对于本例,只需要将上面的三点代入该二次多项式,就能够求得每一项对应的系数值。如果用行列式表达以上步骤,则有:
$$
\displaystyle
\begin{array}{cccc}
p(−2) &=& γ_0 &+& γ_1(−2) &+& γ_2(−2)^2 &=&−1\\
p(0) &=& γ_0 &+& γ_1 (0) &+& γ_2(0)^2 &=& 2\\
p(2) &=& γ_0 &+& γ_1 (2) &+& γ_2 (2)^2 &= &3
\end{array}
$$
接下来将上面的行列式改写成矩阵形式,并利用矩阵求系数:
$$
\begin{pmatrix}
1 & -2 & 4\\
1 & 0 & 0\\
1 & 2 & 4
\end{pmatrix}
\begin{pmatrix}
\gamma_0 \\
\gamma_1 \\
\gamma_2
\end{pmatrix}
=
\begin{pmatrix}
-1 \\
2 \\
3
\end{pmatrix}
$$
根据系数的值,可以得到最终的多项式为:
$$
p(\chi) = 2+ \chi + \frac{1}{4}\chi^2
$$
向量观点下的多项式
现在我们从另外一个角度来看待这个多项式。如果将每一个系数对应的 $\chi$ 的部分作为一个单独的表达式,那么这个多项式实际上是三个部分组成:
- 一个常数方程
- 一个一元一次方程
- 一个二元一次方程
这些基础的多项式被称之为父方程(Parent funtions)。
接下来我们希望对这三个父方程进行离散化(Discretization),也就是使用几个方程曲线上的点(本例是三个点)来表示父方程,然后用这些父方程再来表示目标多项式。
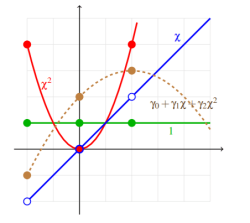
通过将在 X 轴上的 -2, 0, 2(也就是线性方程组中三个点的 X 坐标)代入到父方程中,就能完成这种表示。而这种表示方法又可以转化为下面形式的线性方程组:
$$
\begin{array}{cccc}
p(−2) &=& γ_0(-2)^0 &+& γ_1(−2)^1 &+& γ_2(−2)^2\\
p(0) &=& γ_0(0)^0 &+& γ_1 (0)^1 &+& γ_2(0)^2\\
p(2) &=& γ_0(2)^0 &+& γ_1 (2)^1 &+& γ_2 (2)^2
\end{array}
$$
再将系数提出来:
$$
\begin{pmatrix}
p(−2)\\
p(0) \\
p(2)
\end{pmatrix}
=
γ_0
\begin{pmatrix}
(-2)^0\\
(0)^0 \\
(2)^0
\end{pmatrix}
+
γ_1
\begin{pmatrix}
(-2)^1\\
(0)^0 \\
(2)^1
\end{pmatrix}
+
γ_2
\begin{pmatrix}
(-2)^2\\
(0)^0 \\
(2)^2
\end{pmatrix}
$$
最后将之前的已知的点代入到上面的式子里,就有:
$$
\begin{pmatrix}
-1\\
2 \\
3
\end{pmatrix}
=
γ_0
\begin{pmatrix}
1\\
1\\
1
\end{pmatrix}
+
γ_1
\begin{pmatrix}
-2\\
0 \\
2
\end{pmatrix}
+
γ_2
\begin{pmatrix}
4\\
0 \\
4
\end{pmatrix}
$$
从列方向来看,也就是每一个纵列对应了一个使用三点表示的父方程。而我们注意到每一个纵列都是一个列向量。因此,使用父方程的上的点表示目标多项式的问题,就转化为了如何使用上述的列向量表示目标多项式的问题。
根据本例,这个问题就是通过什么样 $\gamma$ 的值,才能使代表 $\chi$ 的向量表示(组合为)目标多项式向量(这里是 $(-1,2,3)^T$)。
在数学上,我们将通过一系列离散的点来求得范围内的新数据点的方法称为插值(Interpolation)。因此,对于多项式的插值,可以有如下两种解释:
- 将多项式描述为一系列满足线性方程组的点的集合
- 将多项式描述为一个线性组合,该组合的向量(代表父方程)可以产生用于表示多项式的向量。
多项式的点与解
接下来让我们尝试往上述的多项式中添加新的点。
先来尝试一个点 $(2,4)$。我们直接将该点代入到多项式的方程中,然后再写成如下矩阵的形式:
$$
\begin{pmatrix}
1 & -2 & 4\\
1 & 0 & 0\\
1 & 2 & 4\\
1 & 4 & 16
\end{pmatrix}
\begin{pmatrix}
\gamma_0 \\
\gamma_1 \\
\gamma_2
\end{pmatrix}
=
\begin{pmatrix}
-1 \\
2 \\
3 \\
2
\end{pmatrix}
$$
按照矩阵的划分,上述的矩阵实际上可以划分为两部分:
$$
\begin{pmatrix}
1 & -2 & 4\\
1 & 0 & 0\\
1 & 2 & 4
\end{pmatrix}
\begin{pmatrix}
\gamma_0 \\
\gamma_1 \\
\gamma_2
\end{pmatrix}
=
\begin{pmatrix}
-1 \\
2 \\
3
\end{pmatrix} \tag{1}
$$
$$
\begin{pmatrix}
1 & 4 & 16
\end{pmatrix}
\begin{pmatrix}
\gamma_0 \\
\gamma_1 \\
\gamma_2
\end{pmatrix}
=
\begin{pmatrix}
2
\end{pmatrix}\tag{2}
$$
因为我们之间已经验证过了线性方程组 1 是成立的。那么现在只需要验证线性方程组 2 是否成立,就能得知添加的点是否在目标多项式的曲线上了。当然,方程组 2 是成立的。根据之前的信息来做一下总结:
- 点 $(2,4)$ 可以表示多项式上的点。
- 点 $(2,4)$ 满足多项式的向量观点,即使用 $\gamma$ 与对应的向量组合出代表多项式的向量。
我们称这样满足多项式条件的点(无论从哪个观点来看)为多项式的解。如果通过线性组合的观点来看待是否有解无解,则就是看某个线性组合是否能表示代表多项式向量。
鉴于线性组合与列向量的联系,我们可以通过讨论列向量来讨论方程的解的问题。
线性方程组:解的情况
线性方程组的解情况如下:
- 无解
- 有解
- 有唯一解
- 有多个解
- 有无限解
解不唯一的例子
$$
\left( \begin{array}{r r r} 2 & -4 & -2 \\ -2 & 4 & 1 \\ 2 & -4 & 0 \end{array} \right) \left( \begin{array}{c} \chi _0 \\ \chi _1 \\ \chi _2 \\ \end{array} \right) = \left( \begin{array}{r} 4 \\ -3 \\ 2 \end{array} \right)
$$
这个方程组有很多解:比如 $(1,0,-1)^T, (3,1,-1)^T, (-1,-1,-1)^T$ 等等。
方程组无解
把上面的方程组稍微改一改,就求不到解了:
$$
\left( \begin{array}{r r r} 2 & -4 & -2 \\ -2 & 4 & 1 \\ 2 & -4 & 0 \end{array} \right) \left( \begin{array}{c} \chi _0 \\ \chi _1 \\ \chi _2 \\ \end{array} \right) = \left( \begin{array}{r} 4 \\ -3 \\ 3 \end{array} \right)
$$
为什么?我们用高斯变换对其求解,然后在某一步发现了这样的情况:
$$
\left(
\begin{array}{ccc|c}
2 & 2 & −2 & 0\\
0 & −1 & 2 & 3\\
0 & 0 & 0 & 1
\end{array}
\right)
$$
注意最后一行。我们在对角线上发现了 0。因为是最后一行,我们也不能置换行来继续运算。而如果将上述结果与未知数 $\chi$ 结合在一起的话,就会得到一个挺好笑的等式:
$$
0 = 1
$$
想象一下,我们要怎么取 $\chi_0, \chi_1$ 的值,才能使 $ 0 = 1$? Never。因此,我们可以判断,该方程无解。
If Gaussian elimination (with row exchanges) or Gauss-Jordan (with row exchanges) introduces an inconsistent equation ($0 \neq 0$), the system has no solution.
方程组有很多解
来看看下面的例子:
$$
\left(
\begin{array}{c c c|c}
2 & 2 & -2 & 0\\
-2 & -3 & 4 & 3\\
4 & 3 & -2 & 3
\end{array}
\right)
$$
使用高斯-约当方法消元后,我们能得到如下的结果:
$$
\left(
\begin{array}{c c c|c}
1 & 0 & 1 & 3\\
0 & 1 & -2 & 3\\
0 & 0 & 0& 0
\end{array}
\right)
$$
注意看最后一行的等式:
$$
0 = 0
$$
这是个恒等式!因此,不管 $\chi_2$ 取什么值,都不会影响这个等式。我们将 $\chi_2$ 这样的变量,称为自由变量(Free variable),而将 $\chi_0,\chi_1$ 这种受到等式约束的变量,称为因变量(Dependent variable)。由上述得知,要知道$\chi_0,\chi_1$ 的值有什么限制,只能从前两个等式入手了。
因为 $\chi_2$ 不影响第三行恒等式的成立,因此 $\chi_2$ 取什么值都可以。不妨设 $\chi_2 = \beta$,将之前高斯-约当变换得到的结果与 $\chi$ 组合在一起,则有:
$$
\begin{array}{r r r}
χ_0 + χ_2 = 3\\
χ_1 − 2χ_2 = −3\\
χ_2 = β
\end{array}
$$
将 $\beta$ 带入第一个和第二个等式,并挪到等式右边:
$$
χ_0 = 3 − β\\
χ_1 = −3 + 2β\\
χ_2 = β
$$
将上面的结果写成向量的形式,则有:
$$
\left( \begin{array}{r} \chi_0 \\ \chi_1 \\ \chi_2 \end{array} \right)
=
\left( \begin{array}{r} 3 \\ -3 \\ 0 \end{array} \right)
+
\beta \left( \begin{array}{r} -1 \\ 2 \\ 1 \end{array} \right)
$$
我们将上面这种向量形式的结果称为 General solution。来看看为什么这么叫:
- 将上式中的 $(3,-3,0)^T$ 代入到本小节开头的 append matrix 中,结果正好是 $(0,3,3)^T$
- 将上式中的 $(-1,2,1)^T$ 代入同样的矩阵乘法中,结果正好是 $(0,0,0)^T$
这就意味着,我们可以将矩阵乘法的解,按照不同的功能,分成两个部分:
- 第一部分(不含 $\beta$)给出了方程正确的解
- 第二部分(含 $\beta$)将方程映射到了 $0$
因为含 $\beta$ 部分的向量,永远都将矩阵映射到 0 向量,因此无论 $\beta$ 有什么样的值,都不会影响该方程组的解。基于 $\beta$ 的无限取值范围,我们认定这样的方程组有无限多个解。
If Gaussian Elimination or Gauss-Jordan elimination breaks down without introducing an inconsistent equation ($0=0$),then an infinite number of solutions exist.
求解的一般过程
我们将之前学到的向量形式做如下的拆分:
/*前提*/
令 AXs = b, AXn = 0
也就是:
Xs 为 Ax = b 的特殊解
Xn 为 mapping A 到 0 的向量
/*只有特殊解*/
对 A(Xs+Xn),有:
A(Xs+Xn) = AXs = b
/*无限多解*/
A(Xs + βXn) = AXs + β*AXn = b- 首先通过 $A\chi_s = b$ 找到特殊解
- 如果有需要,再通过 $A\chi_n = 0$ 求出方程组的一般解形式
在求解的过程中有几个关键点:
- 可以通过批量求解的方式将 b 和 0 组合到一起进行高斯(高斯-约当)变换
- 当存在无限多解的情况下:
- 当求特殊解的时候,令 $\chi = 0$ 是个很方便的选择($\chi$ 指自由变量)
- 当求一般解的时候,令 $\chi = 1$ 是个很方便的选择
集合 Set
Notation
/*concepts of set*/
Set: a collection of distinct objects
objects: the elements of the set
/*notations*/
x ∈ S // x 是 集合 S 的元素
{x,y,z} // S contains x,y,z, order doesn't matter
|S| // size of S, 不同元素的数量
S ⊂ T // S is a subset of T
S ⊂ T ⇔ (x ∈ S ⇒ x ∈ T) //子集的元素也是父集的元素Operation
S ∪ T //并集 Union,{x| x ∈ S ∨ x ∈ T}
S ∩ T //交集 Intersection, {x| x ∈ S ∧ x ∈ T}
T \ S //complement , {x| x ∉ S ∧ x ∈ T}Vector Space
什么是向量空间
向量空间(Vector Space)是由无限多个向量组成的集合的子集。也就是说,我们可以使用向量空间中的向量来描述无限多的向量(\mathbb{R}^n)。向量空间有如下的性质:
- 0 向量(n 维)属于向量空间
- 如果 向量 $v, w$ 属于向量空间,那么 $(v+w)$ 也属于向量空间
- 如果 $a \in R$,$v$ 属于向量空间,那么 $av$ 属于向量空间
也就是说,一切向量都可以使用向量空间中的向量,通过相加或数乘的方式得到。这两种操作属于初等变换(Elementary Transformation)的一部分。
Subspace
子空间的判断是通过向量空间的性质来判定的。
实例
下列 $\mathbb{R}^3$ 的子集是否是向量空间?
$$
\left\{ x \left\vert x = \left( \begin{array}{c} 0 \\ \chi _1 \\ \chi _2 \end{array} \right) \right. \right\}
$$
详细解答:
1. 判断该空间是否包含同维的零向量。
我们观察到 $\chi_1,\chi_2$ 同时为 0 的时候 $x$ 为零向量,因此零向量属于该子空间。
2. 判断 $x+y$ 是否属于子空间。
令 $x = \left( \begin{array}{c} 0 \\ \chi _1 \\ \chi _2 \end{array} \right), y = \left( \begin{array}{c} 0 \\ \psi _1 \\ \psi _2 \end{array} \right)$。我们观察到:
$$
x + y = \left( \begin{array}{c} 0 \\ \chi _1 + \psi _1 \\ \chi _2 + \psi _2 \end{array} \right)
$$
我们发现 $x +y $ 得到的结果和 $x,y$ 的形式是一样的, $x,y$ 所属子空间是由向量形式像 $x,y$ 一样的向量组成的,既然$x+y$ 可以表示为这样形式的向量,那么 $x+y$ 也是属于该子空间的。
3.判断 $ax$ 是否属于子空间。
$$
\alpha x = \left( \begin{array}{c} 0 \\ \alpha \chi _1 \\ \alpha \chi _2 \end{array} \right)
$$
证明 $ax$ 同样属于子空间。
The Column Space
在说明什么是列空间(Column Space)之前,我们先来看一个特殊的子空间:$\{Ax | x \in \mathbb{R}^n \}$。通过如下的证明很容易明白这是一个子空间:
- 令 $x=0$,有$Ax=0$
- $A(x+y) = Ax + Ay$
- $A(ax) = aAx$
为什么要提出这个子空间?我们之前一直在研究的是 $Ax=b$; 因此,$\{Ax | x \in \mathbb{R}^n \}$ 实际上就是所有 $b$ 的集合。因此,只要 $Ax$ 是有解的,那么 $b$ 必定属于 $\{Ax | x \in \mathbb{R}^n \}$ 这个子空间。而我们将这个子空间,称为 $A$ 的列空间,记做$\mathcal{C}(A)$。正式的定义如下:
Let $A ∈ \mathbb{R}^{m×n}$. Then the column space of $A$ equals the set $\{Ax | x ∈ \mathbb{R}^n\}$.
上述列空间的重要性质定义如下:
Let $A ∈ \mathbb{R}^{m×n}$, $x ∈ \mathbb{R}^n$, and $b ∈ \mathbb{R}^m$. Then $Ax = b$ has a solution if and only if $b ∈ \mathcal{C}(A)$
为什么要叫列空间呢?以列观点看待 $Ax=b$ ,就可以知道 $Ax$ 实际上就是 $A$ 中的列与 $x$ 中的分量组成的线性组合。
The Null Space
在之前的内容中,我们将线性方程组 $Ax=b$ 的通用解的形式表示成了两个部分:特殊解 $X_s$,mapping to 0 的部分 $X_n$。当 $Ax=0$ 的时候我们知道方程组是有无穷多解的。也就是说,$Ax=0$ 的解是一个由无穷多向量组成的集合。我们将这个集合称为零空间(The Null Space),记做$\mathcal{N}(A)$来看一下正式的定义:
Let $A ∈ \mathbb{R}^m×n$. Then the set of all vectors $x ∈ \mathbb{R}^n $ that have the property that $Ax = 0$ is called the null space of $A$ and is denoted by $\mathcal{N}(A) = \{x|Ax = 0\}.$
Span and more
Span
张成空间(Span)的概念非常简单:
- Span 是一个 Set
- Set 里面都是由 Span 指定的向量通过线性变换(初等变换)产生的新向量
我们知道:
- 矩阵可以描述成列向量的集合
- 矩阵与向量的乘积可以描述为线性组合
- 矩阵与向量乘积的集合可以描述为列空间
因此我们可以得出一个结论:Span 就是其指定向量集合(矩阵)的列空间。
Linear Independence
Span 的概念告诉我们,我们可以通过有限个向量的组合,描述出一个包含无限向量的子空间的。因此,我们很有必要找出哪些向量是描述空间必要的向量。来看一个下面的例子:
$$
{\rm Span}\left( \left( \begin{array}{r} 1 \\ 0 \\ 1 \end{array} \right) , \left( \begin{array}{r} 0 \\ 0 \\ 1 \end{array} \right) \right) = {\rm Span}\left( \left( \begin{array}{r} 1 \\ 0 \\ 1 \end{array} \right) , \left( \begin{array}{r} 0 \\ 0 \\ 1 \end{array} \right) , \left( \begin{array}{r} 1 \\ 0 \\ 3 \end{array} \right) \right)
$$
这两个张成空间实际上是等价的;因为我们可以使用向量 $\left( \begin{array}{r} 1 \\ 0 \\ 1 \end{array} \right)$ 和 $\left( \begin{array}{r} 0 \\ 0 \\ 1 \end{array} \right)$ 通过初等变换组合出向量 $\left( \begin{array}{r} 1 \\ 0 \\ 3 \end{array} \right)$。那么很显然如果要描述上述的空间,$\left( \begin{array}{r} 1 \\ 0 \\ 3 \end{array} \right)$ 就是不必要的一个向量了。
那么要怎么样表示“用于表示某个空间的集合中,每一个向量都是不可缺少的呢”?这就是我们要谈到的线性无关(Linear Independent)。先来看看定义:
Let $\{v_0,..., v_{n−1}\} ⊂ \mathbb{R}^m$. Then this set of vectors is said to be linearly independent if $χ_0v_0 + χ_1v_1 + ··· +χ_{n−1}v_{n−1} = 0$ implies that $χ_0 = ··· = χ_{n−1} = 0$.
如果某个向量组不是线性无关的,那么它就是线性相关(Linear dependent)的。
为什么要这么定义?我们来反证一下:
假设 $\{ a_0, a_1 , \ldots , a_{n-1} \} \subset \mathbb {R}^ m$ 这个集合线性相关。那么必然存在一个向量组 $\chi _0, \chi _1, \ldots , \chi _{n-1} \in \mathbb {R}$,使得 $\chi _0 a_0 + \chi _1 a_1 + \cdots + \chi _{n-1} a_{n-1} = 0$ 至少存在一个元素 $X_j \neq 0$(线性无关的条件是所有 $X$ 都必须等于 0)。因此,我们将 $X_ja_j$ 放到上述等式的右边,则有:
$$\chi _ j a_ j = - {\chi _0} a_0 + - {\chi _1} a_1 - \cdots - {\chi _{j-1}} a_{j-1} - {\chi _{j+1}} a_{j+1} - \cdots - {\chi _{n-1}} a_{n-1}
$$
因为 $X_j$ 不为 0,两边同时除以 $X_j$,则有:
$$
a_ j = - \frac{\chi _0}{\chi _ j} a_0 + - \frac{\chi _1}{\chi _ j} a_1 - \cdots - \frac{\chi _{j-1}}{\chi _ j} a_{j-1} - \frac{\chi _{j+1}}{\chi _ j} a_{j+1} - \cdots - \frac{\chi _{n-1}}{\chi _ j} a_{n-1} .
$$
这就意味着,在给定的集合中,至少有一个向量可以用别的向量表示。那么反过来,如果要保证所有的向量不能互相表示,则需要满足线性无关的定义。
线性无关与零空间
线性无关与零空间有以下的关系:
Let $\{a0,...,a_{n−1}\} ⊂ \mathbb{R}^m$ and let $A = (a_0|\cdots|a_{n-1})$. Then the vectors $\{a_0,...,a_{n−1}\}$ are linearly independent if and only if $\mathcal{N} (A) = {0}$.
简易的证明:
/*充分性*/
假设 {a0...an-1} 是线性无关的
令 x ∈ N(A)
Ax = 0 ⇒ 线性组合中所有系数 $\chi$ 都为 0 //线性无关的定义
因此 x = 0
因此 N(A) = 0 //因为 Ax 只能得到 0
/*必要性(反证)*/
假设 {a0...an-1} 线性相关
那么必然存在 {X0...Xn-1} 至少有一个元素 Xj ≠ 0
令 Ax = 0,则Xj ∈ N(A)
因此 N(A) ≠ 0- 单位矩阵线性无关
- 三角矩阵线性无关
Basis for Subspaces
首先看概念。基(Basis)指的是一个线性无关的向量组里包含的所有向量。
这个定义很形象,因为线性无关的向量组中每一个向量都是独一无二的,而通过他们的组合能得到表示整个空间的向量。因此,可以将线性无关向量组里的向量想象成建造空间的基石,相信这也是基这个概念的由来吧。
基的个数不超过空间的维度
这是一个很有用的推论:
Let $S ⊂ \mathbb{R}^m$. Then $S$ contains at most $m$ linearly independent vectors.
证明过程:
/*反证*/
假设 S 包含的线性无关的向量大于 m
则可知 S 至少包含 m+1 线性无关的向量
那么 S 的向量组可以写成:{v0, v1,..., vm−1, vm}.
令 V = (v0 | v1| ... | vm−1 | vm)
因此该矩阵 V 是一个 m * (m + 1) 的矩阵
因此,该矩阵代表的行列式中,未知数的数量(m+1)大于关系的数量 m
那么至少有一个未知数是不确定的
因此,线性方程组存在无穷多个解
也就是说,可以找出一个非 0 的解 Xn,使得 VXn = 0
这与 {v0, v1,..., vm−1, vm} 线性无关的定义矛盾
得证非平凡子空间一定有基
这个定理是上面的推论,具体的说应该是:
若存在非平凡子空间 $S \in \mathbb{R}^m$,则必定存在一组数量有限的基 $\{ v_0, v_1, \ldots , v_{n-1} \} \subset \mathbb {R}^ m$,使得 $Span\{ v_0, v_1, \ldots , v_{n-1} \} = S$
非平凡子空间(Non-trivial Space)指该子空间不仅仅由零向量组成。
证明过程:
首先由 5.31 的推论得知, n ≤ m
令 S 为非平凡子空间
∴ S 包含至少一个非零向量
令 v0 为该向量
∴ Span(v0) 不为空且 S\Span(v0) 不为空 //某些向量不在 Span(v0) 中,但是在 S 中。因为 Span(v0) 只是由 v0 张成的空间, S 里面可能还会有 v1 v2 v3 等等。
我们接着往 Span 中添加 S 中不属于 Span 的向量,比如 Span(v0) ⇒ Span(v0,v1)
∴ 添加一次,Span 就能 表示更多 S 中的向量
按此循环下去,由于 S 中的向量有限,所以可以循环到 S 的向量取空的一天
∴ 最终 Span 可以完全表示 S
∴ 肯定存在一组基使得 Span 可以完全表示 S子空间的维度 / Rank
根据 5.3.2 的推论,每个平凡子空间都存在一组基可以表示其自身。显而易见的是,基并不是唯一的(比如我们可以给所有基乘上一个常数,这些基依然可以表示子空间内所有向量)。但基的数量一定是固定的。而基的数量,我们就称为子空间的维度,也称为子空间的秩(Rank)。来看下正式的定义:
Let $S$ be a subspace of $\mathbb{R}^m$ and let $\{v_0, v_1,···, v_{n−1}\} ⊂ \mathbb{R}^m$ and $\{w_0,w_1,···,w_{k−1}\} ⊂ \mathbb{R}^m$ both be bases for $S$. Then $k = n$. In other words, the number of vectors in a basis is unique.
证明过程:
/*反证*/
令 k > n
令 V = (v0 | v1| ... | vn−1)
令 W = (w0 | w1| ... | wk−1)
令 X = (x0 | x1| ... | xk−1)^T
∴ 存在 wj = Vxj // V 张成了 S,W 属于 S,因此一定能找到用 v 表示 w 的方法,也就是 V 和 X(系数) 的线性组合表示 W
∴ W = VX
为了匹配 V 的列数 n,X 中每个向量的大小也应该是 n
所以 X 是一个 n*k 的矩阵
因为 k > n
∴ 如果将 X 视作线性方程组,那么 X 有无穷多解
也就是 N(X) 中存在不等于 0 的向量 y
∴ Wy = VXy = V(Xy) = V(0) = 0
W 中必定含有非零的向量
这与 W 是子空间 S 的基矛盾 //基必须是线性无关的向量组
得证相关资料
- 非 SVG 图来源于 LAFF