Matrix Algebra for Engineers

Week 3 Notes

向量空间 Vector space 由一系列的向量（Vector）和一系列的标量（Scalar）组成。向量空间必须是封闭的（closed），也就是，通过缩放向量（scalar multiplication），相加向量（vector addition），得到的向量最终也属于该向量空间。比如在一个 $3 \times 1$ 的向量空间中，选取任意一个向量与任意标量相乘，然后再加到任意另外一个向量上，得到的结果必定是一个 $3 \times 1$ 的向量。

Linear Independence 的正式定义如下：

Let $\{v_0,..., v_{n−1}\} ⊂ \mathbb{R}^m$. Then this set of vectors is said to be linearly independent if $χ_0v_0 + χ_1v_1 + ··· +χ_{n−1}v_{n−1} = 0$ implies that $χ_0 = ··· = χ_{n−1} = 0$.

上面的定义实际上讨论的问题是，向量空间中，是否至少存在一个向量，可以用其他的向量来表示。而 Linear Independence 意味着所有的向量都无法用任何其他向量来表示。换句话说，只有在所有向量的系数都为 $0$ 的情况下，向量的和才能为 $0$。如果有可以互相表示的向量，他们就可以通过更改自身的系数来进行相互抵消。

判断 Linear Independence 可以通过 RREF 来进行判断：

1. 首先将向量空间中的向量组成矩阵
2. 求该矩阵的 RREF
3. 如果 RREF 是 Indentiy Matrix，那么该组向量是线性无关的。

下面的向量空间就是线性无关的： $$ \left (\begin{pmatrix} 3\\ 3\\ 2 \end{pmatrix} \begin{pmatrix} 2\\ 1\\ 1 \end{pmatrix} \begin{pmatrix} 1\\ 2\\ 0 \end{pmatrix} \right ) \Rightarrow \begin{pmatrix} 3& 2& 1\\ 3& 1& 2\\ 2& 1&0 \end{pmatrix} \Rightarrow \begin{pmatrix} 1& 0& 0\\ 0& 1&0 \\ 0& 0 &1 \end{pmatrix} $$

• Span（张成空间），指基于给定的向量空间中的几个向量所能生成的向量空间
• Basis：该向量空间仅由 Basis 即可张成（即任意向量空间中任意向量都可以由 Basis 得到）。Basis set 中的向量必须是线性无关的。
• Dimension：向量空间中的 Basis 的数量（唯一）

Gram-Schmidt process 是一种通用的，将非 orthonormal basis 转换为 orthonormal basis 的算法。其主要的步骤分两步：

1. 以源 basis 所在向量空间中的某一个 basis 作为基准，构造与其垂直的向量
2. 将该向量进行 Normalize，则可得到对应的 orthonormal basis。

如上图，假设初始两个 basis 为 $V_1$ 和 $V_2$：

首先选择其中一个 basis 作为 orthonormal basis 的基准，这里选择 $V_1$，令新 basis $u_1 = V_1$

确定了新的基准 basis 后，需要求出与其垂直的向量的表达式。通过观察发现，如果做 $V_2$ 到 $u_1$ 上的投影，那么垂直方向上的向量 $u_2$ 是与 $u_1$ 垂直的。

令 $V_2$ 在 $u_1$ 上的投影向量为 $s_1$，根据向量的加减法，可得： $$ u_2 = V_2 - s_1 $$ 由于 $s_1$ 是 $V_2$ 在 $V_1$ 上的投影向量，因此可以写成： $$ ks_1 = u_1 $$ 因此，只需求出标量（magnitude） $k$，即可得到 $s_1$。因为 $u_2$ 与 $u_1$ 正交，因此 $u_2 \cdot u_1 = 0$。将 $u_2 = V_2 - s_1$ 带入该式，有： \[ \begin{align*} &(V_2 - u_1) \cdot u_1 = 0 \\ \Rightarrow & (V_2 - ks_1) \cdot u_1 = 0 \\ \Rightarrow & V_2 \cdot u_1 - ku_1\cdot u_1 = 0 \\ \Rightarrow & k = \frac{V_2 \cdot u_1}{u_1 \cdot u_1} \end{align*} \] 带入之前的 $u_2$ 表达式，最终可以得到 $u_2$ 如下：

$$u_2 = V_2 - \frac{(V_2 \cdot u_1)u_1}{u_1 \cdot u_1} $$

代数上，点积一般表达为行向量与列向量的相乘形式。因此，上面的公式可以将点积部分进行改写（因为得到的都是常数，因此书写方式不影响结果）

$$u_2 = V_2 - \frac{(u_1^T \cdot V_2)u_1}{u_1^T \cdot u_1} $$

在代数上，如果 $u_1$ 与 $u_2$ 正交，那么有： $$ u_1^T \cdot u_2 = 0 $$ 根据该性质，我们对本节第一个公式的两边同时乘以 $u_1^T$，有： \[ \begin{align*} u_1^Tu_2 & = u_1^TV_2 - \frac{u_1^T(u_1^T \cdot V_2)u_1}{u_1^T \cdot u_1} \\ &=u_1^TV_2 - \frac{(u_1^T \cdot V_2)(u_1^Tu_1)}{u_1^T \cdot u_1} \\ &=u_1^TV_2 - u_1^TV_2 \\ & = 0 \end{align*} \] 因此，这样的 $u_2$ 表达式可以确保 $u_1$ 和 $u_2$ 是 orthagonal basis。

求 orthagonal basis 在多维度的向量上的操作也是相同的；我们只需要将向量按二维空间进行拆分讨论即可。比如处于 $x,y,z$ 的三维向量，如果以 $x$ 为基准求一个新的 orthagonal basis，那么只要分别求 $x,y$ 与 $x,z$ 平面中的 orthagonal basis 即可；也就是就是已知 $u_1$，分别用 $u_1$ 表示 $u_2$ 和 $u_3$。从计算上来看，就是使用基准向量分别减去不同的 $s_1$，即：



\[ \begin{align*} u_3 & = V_3 - \frac{(u_1^T \cdot V_3)u_1}{u_1^T \cdot u_1} - \frac{(u_2^T \cdot V_3)u_2}{u_2^T \cdot u_2} \\ \end{align*} \]

标准化向量的过程套用 norm 公式即可： $$ u_n = \frac{u_n}{\sqrt{u_n^Tu_n}} $$

矩阵 $A$ 的Null Space 指对于矩阵 $A$，满足 $Ax = 0$ 的所有 $x$ 组成的向量空间。Null Space 中的向量同样是初等变换下封闭的，即其内部的向量通过乘法和加法得到的向量也在 Null Space 中。

求 Null Space，只需要知道它的 basis 就可以了。从代数上来上，我们可以从 $Ax = 0$ 的非特殊解入手（也就是 free variable，即取什么值都不会影响 $Ax=0$ 的那一部分未知数）

• 将 $A$ 转化为 RREF
• 根据 RREF 的结果，找出 $Ax = 0$ 的非特殊解与特殊解（也就是我们说的 basic variable)之间的关系。通常，pivot 所在位置的未知数是特殊解。因此：
  • 找到 pivot
  • 由 $Ax = 0$，可知 $A$ 中任意一行与 $x$ 的点乘结果均为 0。利用该关系，列出 basic variable 与 free variable 的关系。
  • 按该关系，最终得到的，以 free variable 表示的 $x$，其对应的向量即为 Null space 的 basis。

假设有如下矩阵 $A$，其 Rref 形式为：
\[ A= \begin{pmatrix} 1& 1& 1& 0\\ 1& 1& 0& 1\\ 1& 0& 1& 1 \end{pmatrix} \Rightarrow Rref(A)= \begin{pmatrix} 1& 1& 1& 2\\ 0& 1& 0& -1\\ 0& 0& 1& -1 \end{pmatrix} \] 根据 $Ax = 0$ 列式。要使乘法有意义，可知 $x$ 是一个 $4 \times 1$ 的向量。设其分量为 $x_1,x_2,x_3,x_4$，有：
\[ \begin{pmatrix} 1& 0& 0& 2\\ 0& 1& 0& -1\\ 0& 0& 1& -1 \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{pmatrix}=0 \] 观察 Rref(A) 的 pviot，发现 $x_4$ 是唯一的 free variable。因此，根据 $Ax = 0$，将 $x_1,x_2,x_3$ 用 $x_4$ 表示：
\[ \begin{cases} & x_1 + 2x_4 &= 0\\ & x_2 - x_4 &=0\\ & x_3 - x_4 &=0 \end{cases} \Rightarrow \begin{cases} & x_1 = -2x_4\\ & x_2 = x_4 \\ & x_3 = x_4 \end{cases} \] 最后根据上面的关系，将向量 $x$ 以 $x_4$ 表示：
\[ x= \begin{pmatrix} -2x_4\\ x_4\\ x_4\\ x_4 \end{pmatrix} = x_4 \begin{pmatrix} -2\\ 1\\ 1\\ 1 \end{pmatrix} \] 此时求得的向量即为需要求得 basis。也就是说，$A$ 的 Null space 是由上述向量张成的向量空间。

Null Space 的一个重要应用是求解 underdetermined system。我们知道，在一个 system 中，如果关系（row）少于未知数（column），那么这个系统就是 underdetermened 的。换句话说，该系统没有特殊解，只有一系列的通用解。

那么 Null space 在里面起到什么样的作用呢？先说结论：

let $u$ be a general vector in $Null(A)$, let $v$ be any vector that solves $Ax = b$, then
$$ x = u + v $$
is the gerneral solution to $Ax = b$

假设 $x = u + v$，那么： $$ Ax = A(u+v) = Au + Av $$ 因为 $u$ 属于 $Null(A)$，因此 $Au= 0$。那么： $$ Ax = Av = b $$ 到此得证。

以下面的 augument matrix 为例。为了求 $x$，我们需要分开求 $u$ 和 $v$。对于 $u$，过程与之前求 basis 的过程一致.先求出其 Rref：
\[ \left ( \begin{array}{cccc|c} -3& 6& -1& 1&-7 \\ 1& -2& 2& 3&-1 \\ 2& -4& 5& 9&-4 \end{array} \right ) \Rightarrow \left ( \begin{array}{cccc|c} 1& -2& 0& -1&-3 \\ 0& 0& 1& 2&-2 \\ 0& 0& 0& 0&0 \end{array} \right ) \] 根据 Rref 可以求出 u。注意，u 只需要各个变量之间的关系，因此用不到增广矩阵最后一列：
\[ \begin{pmatrix} 2u_2+u_4\\ u_2\\ -2u_4\\ u_4 \end{pmatrix} = u_2\begin{pmatrix} 2\\ 1\\ 0\\ 0 \end{pmatrix} + u_4 \begin{pmatrix} 1 \\ 0\\ -2\\ 1 \end{pmatrix} \] 之后我们再来求 $v$。与求 $u$ 不同，$v$ 是一定程度上的特殊解，也就是能确定下来的变量都需要确定下来。因此，需要代入增广矩阵的结果部分：
\[ \begin{cases} v_1-2v_2-v_4&=3 \\ v_3+2v_4&=-2 \end{cases} \] 由于 $v_2$ 和 $v_4$ 是 free variable，因此可以取任何值。我们在这里取 $0$，根据上面的等式即可算出 $v_1$ 和 $v_3$，有：
\[ v=\begin{pmatrix} 3\\ 0\\ -2\\ 0 \end{pmatrix} \] 到此，整个结果可以写为：
\[ x=a \begin{pmatrix} 2\\ 1\\ 0\\ 0 \end{pmatrix} +b \begin{pmatrix} 1\\ 0\\ -2\\ 1 \end{pmatrix} +\begin{pmatrix} 3\\ 0\\ -2\\ 0 \end{pmatrix} \] 其中 $a$，$b$ 代表了 $u_2$, $u_4$ 的解，为任意值。

Colmun Space 是一种将 $Ax$ 以列向量表达出来的方式，比如下面的例子：


通过这样的整理，不难发现矩阵与列向量的乘法，实际上是矩阵中各列的线性组合。通过矩阵 $A$ 各列张成的空间，我们称为矩阵 $A$ 的 colmun space ，记作 $C(A)$

虽然 Column Space 由 $A$ 中列向量张成，但有时 $A$ 中的各个向量并不是 linear independent 的。因此，Column Space 的结果需要用 basis 和维度来体现。我们通过如下两步来进行：

1. 计算 $A$ 的 Rref
2. $Rref(A)$ 中拥有 pivot point 的列都是线性无关的。因此其对应的 $A$ 中的列，则是张成 Column space 的 basis

比如下面的例子：
\[ \begin{pmatrix} 1& 1& 1& 0\\ 1& 1& 0& 1\\ 1& 0& 1&1 \end{pmatrix} \Rightarrow Rref(A) \begin{pmatrix} 1& 0& 0& 2\\ 0& 1& 0& -1\\ 0& 0& 1&-1 \end{pmatrix} \]
将得到的 $Rref(A)$ 对应回 $A$，即可得到张成 $A$ 的 basis：


因此，可知 ：

\[ C(A)=span \left \{ \begin{pmatrix} 1\\ 1\\ 1 \end{pmatrix} \begin{pmatrix} 1\\ 1\\ 0 \end{pmatrix} \begin{pmatrix} 1\\ 0\\ 1 \end{pmatrix} \right \} \]

其空间的维度为 $3$。

与 column space 类似，row space 是以矩阵 $A$ 中的行向量进行线性组合而张成的空间。因为线性组合以列向量为标准，因此 row space 可以被视作矩阵 $A$ 的转置矩阵的 column space，记作 $Col(A^T)$

Left null space 的概念延伸自 null space，指将向量 $x$ 至于 矩阵 $A$ 左边，产生的线性组合结果为 $0$ 的向量所张成的空间，也就是满足 $x^TA = 0$。该等式也可以视作 $x$ 与 $A$ 的转置的相乘，即 $xA^T=0$

• 无论是 row space 还是 column space，他们的维度是不变的。我们将该维度大小称为矩阵的 rank。
• rank 同样可以被视作矩阵中线性无关向量（列）的数量。

假设 $A$ 为 $m \times b$ 的矩阵：

• null space 为 $n \times 1$ 的向量空间的 sub space，因为 null space 是由 $n \times 1$ 的向量 $x$ 进行线性组合得到的。
• column space 为 $m \times 1$ 的向量空间的 sub space，因为其由 $A$ 中列向量线性组合得到。
• row space 为 $n \times 1$ 的向量空间的 sub space。将 row space 考虑为 $Col(A^T)$ 即可。
• left null space 为 $m \times 1$ 的向量空间的 sub space，将 left null space 考虑为 $A^Tx$ 的 null space 即可

Null space 与 Row space 被称为 Orthagonal Complements，因为:

• null space 的维度等于 Non-pivot column 的数量，row space 的维度等于 pivot column 的数量，这两者的维度之和等于 $A$ 中列向量的总数
• 任意 row space 中向量与 null space 中向量垂直。因为 $Ax = 0$，因此 $A$ 中每个行向量与对应 $x$ 向量的点积必然为 0.
• 同时满足以上两个条件的两个向量空间，被称为 Orthagonal Complements。同理可以推断出 left null space 与 column space 也互为 Orthagonal Complements。

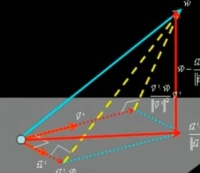
Orthogonal Projection 指将一个在较大的向量空间中的向量，投影到该向量空间的某个 sub space 中的操作。具体来讲，假设我们有：

• $n$ 维的向量空间 $V$
• $p$ 维的向量空间 $W$，$W$ 为 $V$ 的 sub space
• $W$ 的 orthonormal basis ${s_1,s_2,..s_p}$
• $v$ 为 $V$ 中的一个向量

那么 Orthogonal Projection 可以被定义为：

$$ v_{proj_w} = (v^Ts_1)s_1 + (v^Ts_2)s_2+....(v^Ts_p)s_p $$

如果将 orthonormal basis 扩展到基于 $V$，而不是 $W$。假设该 Basis 为：${s_1,s_2,..s_p, t_1, t_2, ...t_{n-p}}$，$t$ 为 $V$ 中额外的 basis。因为 $V$ 为 $n$ 维，因此 $t$ 的总数为 $n-p$。同样设 $v$ 为 $V$ 中向量，那么 $v$ 可以表示为： $$ v = a_1s_1 + a_2s_2... + a_ps_p + b_1t_1+b_2t_2...+b_{n-p}t_{n-p} $$ 其中 $a$ 和 $b$ 为标量。

如果将上面的 $v$ 带入到之前的公式中，那么可以发现，只要 $v$ 中与当前分量不同的项，都会被取消掉。比如 $(v^Ts_1)s_1$，只有在 $v$ 分量为 $a_1s_1$ 时，才会有乘积的结果不为 0。该结果为 $a_1s_1^Ts_1 = a_1$。因为 $s_1$ 与其他项的向量同属一个 orthnormal basis 中，因此只要不是与自身相乘的项均为 $0$，也就是： $$ (v^Ts_1)s_1 = a_1s_1 $$ 那么 $v$ Orthogonal Projection 就可以写成： $$ v_{proj_w} = a_1s_1+a_2s_2...+a_ps_p $$ 这与之前的公式是等价的。

统计学里面有一个经典的问题：The least-sqares problem（linear）。该问题描述的是：给定的一系列点，是否能找到一条直线，使得所有的点到直线距离的平方之和最小？



这个问题实际上可以转换为线性代数的问题。以上图为例，假设图中点有 $n$ 个，都是我们的 data。令每一个点的坐标为： $$ (x_1, y_1), (x_2, y_2)...(x_n,y_n) $$ 假设蓝色直接代表了所有 $x,y$ 的关系，可以设该直线的方程为： $$ \beta_0 + \beta_1x = y $$ 其中 $\beta_0$ 为直线与 $y$ 轴的交点，$\beta_1$ 为斜率。现在将所有的点都带入方程，可得： \[ \begin{align*} y_1=& \beta_0 +\beta_1x_1 \\ y_2=& \beta_0 +\beta_1x_2 \\ ...\\ y_n=& \beta_0 +\beta_1x_n& \end{align*} \] 很明显，这是一个 linear system。在这个 Linear system 中，$x$, $y$ 都是已知的，而 $\beta_0, \beta_1$ 是未知的。因此可以做下面的变型：



则整个问题就转化为了 $Ax=b$ 的问题。

不过，在上述描述的关系中，未知数只有 2 个 $\beta_0, \beta_1$，但相关的等式有 $n$ 个。这种情况被称为 over determined；这种情况下，$\beta_0, \beta_1$ 显然是没有解的。

因此，我们退而求次，希望找一条 “最适合” 的直线来表示所有 $x,y$ 的关系。由于 $Ax$ 的结果必定处于 $A$ 的 column space 中（colmun space 代表 $Ax$ 中的列项量的线性组合，也就是所有可能的解，显然 $b$ 不处于该列空间中），因此，我们将 $b$ （也就是所有 $y$ 组成的向量）投射到 $A$ 的列空间中。根据我们之前根据 Orthogonal Projection 得出的结论，具体的来说，我们应该将 $b$ 投射到 $b_{proj_{col(A)}}$上（该向量与被投射的向量最近，因此得到的误差最小），也就是求下面的解： $$ Ax = b_{proj_{col(A)}} $$

为了求解上述的等式，我们需要对 $Ax=b$ 做一些变形。如果我们将 $b$ 分解为在 $col(A)$ 上的投影 $b_{proj_{col(A)}}$，和另外一个分量，也就是： \[ \begin{align} Ax & = b_{proj_{col(A)}} + b -b_{proj_{col(A)}} \end{align} \] 由于 $b_{proj_{col(A)}}$ 是在 $col(A)$ 的投影，那么 $ b -b_{proj_{col(A)}}$ 显然垂直于 $col(A)$。而通过基础空间之间的关系可知，$col(A) =row(A^T)$。而 row space 恰好又与对应的 null space 互相垂直（互为 Orthagonal completement），因此：

• $ b -b_{proj_{col(A)}}$ 与 $col(A)$ 垂直，因此与 $row(A^T)$ 垂直
• 也就是说， $b -b_{proj_{col(A)}}$ 属于 $null(A^T)$

现在我们对 $Ax=b$ 的两边同时乘以 $A^T$。由于 $A^Tb_{proj_{col(A)}}$ 属于 $null(A^T)$，因此该分量与 $A^T$ 的乘积为 $0$。由此可以得到以下的推论：

\[ \begin{align*} A^TAx & = A^Tb_{proj_{col(A)}} + A^T(b -b_{proj_{col(A)}})\\ &=A^Tb_{proj_{col(A)}} \end{align*} \] 记作：

$$ A^TAx=A^Tb $$

当 $col(A)$ 中的向量是线性无关的时候，$A^TA$ 的结果是一个方阵，是可逆的。因此，对 Normal Equation 可以做出进一步的变形：
\[ \begin{align*} &A^TAx = A^Tb \\ \Rightarrow &x = (A^TA)^{-1}A^Tb \\ \Rightarrow &Ax = {\color{Red} A(A^TA)^{-1}A^T} b = b_{proj_{Col(A)}} \end{align*} \] 标红的部分被称为 Projection matrix。该矩阵将 $b$ 投影到 $Col(A)$ 上。

假设有数据点：$(1,1), (2,3),(3,2)$，求过这几点的 best fit line。

首先，根据数据点，以 $y = \beta_0 + \beta_1x$ 为模板，建立 linear system。通过 linear system 确定 $A$：

\[ \begin{pmatrix} 1&1 \\ 1& 2\\ 1&3 \end{pmatrix} \begin{pmatrix} \beta_0\\ \beta_1 \end{pmatrix} = \begin{pmatrix} 1\\ 3\\ 2 \end{pmatrix} \] 将 $A$ 带入 normal equation： \[ \begin{pmatrix*} 1& 1& 1\\ 1& 2&3 \end{pmatrix*} \begin{pmatrix*} 1&1 \\ 1& 2\\ 1&3 \end{pmatrix*} \begin{pmatrix*} \beta_0\\ \beta_1 \end{pmatrix*} = \begin{pmatrix*} 1& 1& 1\\ 1& 2&3 \end{pmatrix*} \begin{pmatrix*} 1\\ 3\\ 2 \end{pmatrix*} \]
计算后得到关于 $\beta_0$ 和 $\beta_1$ 的 linear system。此时的未知数与等式数量相同，因此可以求解：
\[ \begin{pmatrix*} 3 &6 \\ 6 &14 \end{pmatrix*} \begin{pmatrix*} \beta_0\\ \beta_1 \end{pmatrix*} = \begin{pmatrix*} 6\\ 13 \end{pmatrix*} \]
解得 $\beta_0 = 1$，$\beta_1 = 1/2$，因此得到的直线方程为 $y = 1 + 1/2 * x$