目录
Frequency Distributions
S.B.S book Chapter 2 notes
Intro to Frequency Distribution
当收集到数据之后,如何组织并呈现这些数据就变得非常重要。对于大量数据来说,图表 / 表格类型的数据能更好的呈现数据的特点,而这也是描述性统计学需要处理的问题之一。频数分布表(Frequency distribution table)就是一种主要呈现数据的手段。
A frequency distribution is an organized tabulation of the number of individuals located in each category on the scale of measurement.
频数分布表将数据中的每个类别及个体数量按照分数从高到低排列。通常频数分布表可以被表现表格或者图,但无论表现形式如何,频数分布表都会有如下两个特点:
- 测量尺度由类别组成。
- 每一个类别下都会有一组频率(或者该类别下个体的数量)的记录。
因此,频数分布表实际上是一张呈现了个体在特定测量尺度下的分布的图;因此被称为频数分布表。
Frequency Distributions Tables
来看一个最简单的频数分布表。假设我们有 $N=20$ 的如下数据:
$$8,9,8,7,10,9,6,4,9,8,7,8,10,9,8,6,9,7,8,8$$
根据频数分布表的定义,我们将该表分为两部分:
- $X$,即每个个体的分数
- $f$,每个个体的出现的次数
那么该表制作的步骤如下:
- 将所有个体按 $X$ 的值从高到低排序
- 将每个个体对应出现的次数写到对应的 $f$ 里
通过频数分布表计算总分数
推荐的计算$\sum X$ 的方法有:
- 还原所有的个体,依次按求和表达式中的式子求出对应的值,再累加(可以应用到所有求和)
- 先将分数与对应的出现次数相乘,再累加
Proportions and Percentages
比起 $f$,我们还有两种更直观的数据可以呈现出不同类别的个体在总体中分布,他们就是比例(Proportions )和百分比(Percentages)。
令某类别的个体所占总体数量的比例为 $p$,显然有:
$$
p = f/N
$$
而百分比则可以表示为:
$$
\% = p(100) = 100 * \frac{f}{N}
$$
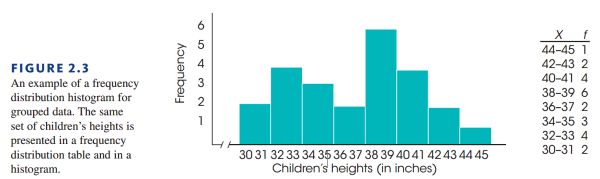
Grouped Frequency Distribution Tables
实际处理中我们面对的数据往往具有非常广的范围。一个例子就是我们的百分制分数,如果以分为精度,那么分数的范围是从 0-100。如果按照频数分布表的制作方法来处理这些数据,我们会发现我们的表会有 100 多行。
这样显然违背了我们制作频数分布表的初衷:组织数据使其能够能简单清除的呈现数据。因此,对于数据范围非常广的数据,我们可以先对其分数进行分组,再将每组的区间作为行内容呈现到频数分布表中。这种通过以组为单位呈现频数分布的表,我们称为分组频数分布表(\\Grouped Frequency Distribution Tables\\)。
分组频数分布表并没有特殊的要求,但一般而言我们遵循以下的方式来设计该表:
- 若无特殊要求,分数的分组分为 10 组。10 组是一个很好的数量,多了会影响观测,少了会丢失信息。
- 每组的区间宽度最好是一个简单的数字;比如百分制的分数,就可以以 10 分为一个区间;这样计算起来非常方便。2、5、10 都是非常好的选择。
- 每个分组的下界最好是区间宽度的整数倍。比如百分制分数按 10分 一个阶段分组,我们就可以以 10分、20分、30分等等作为每组的起点。
- 每个组的区间应该相同。
还有一些相关策略:
- 利用试错策略求出合适的区间宽度。比如 $N=50$,我们可以同时尝试 2,5,10,发现 5 最合适。
- 从最低数出发,找一个宽度的整数倍的数作为起点,使最低数处于该起点往后一个区间宽度的区间之内,然后累加。
Real Limits and Frequency Distributions
需要注意的是,如果频数分布表中处理的数据是连续变量,那么实际每个分数表示的是一个区间。这个区间是分数加减 real limit 的一半。因此,频数分布表中的 $f$ 在这里代表的是有多少分数处于这个区间。
这个概念可以推广到分组频数分布表。对于连续变量的分组频数分布表,其表示的实际区间应该是:
$$
[区间起始点 - real limit / 2, 区间起始点 + 区间宽度 + real limit / 2]
$$
举个例子,如果按秒作为精度,那么表示 40-49 秒的区间的组,实际上包含了 $[39.5, 49.5]$ 这个区间的所有分数。
Frequency Distribution Graphs
频数分布图(Frequency Distribution Graphs)是另一一种反映频数分布的手段,其内容可以从频数分布表中找到。常见的频数分布图由两条相互垂直的坐标轴组成,水平方向的为 $X$ 轴,代表了 $X$,从左到右数值增大;竖直方向上的轴为 $Y$ 轴,代表了 $f$,从下到上数值增大。
Graphs for Interval or Ratio Data
当数据中包括数字数据,并且这些数据通过等距 / 等比量表来衡量的时候,我们可以通过两种图来表示该数据的频数分布。
Histogram
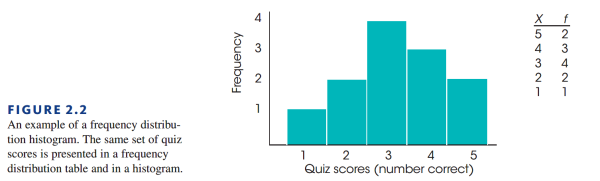
第一种我们称为直方图(Histogram):
- 普通列表项目直方图由一个个的 “bar” 组成
- 每个 “bar” 的宽度代表了数据的区间(离散数据就是一个数值)
- 每个 “bar” 的高度代表了该类别数据的频率。
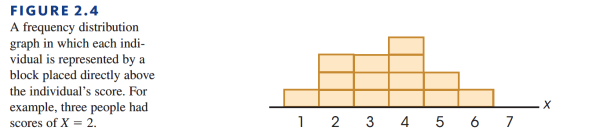
Modified Histogram
Polygons
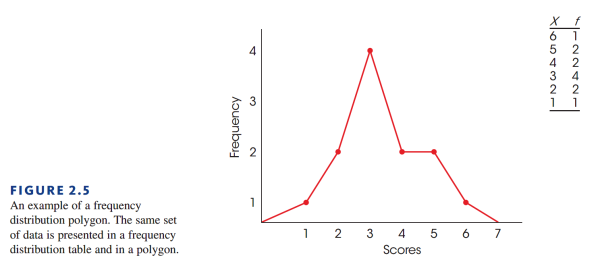
第二种图我们称之为折线图(Polygon)。下面是如何画一个折线图:
- 将所有的分数在 $X$ 上一一列出
- 处于每个分数正上方的点代表了该类数据的频数
- 然后将频数按点为单位连接起来
- 折线图在最左边和最右边都会与 $X$ 相交,相交的点正好处于分数范围外一个单位
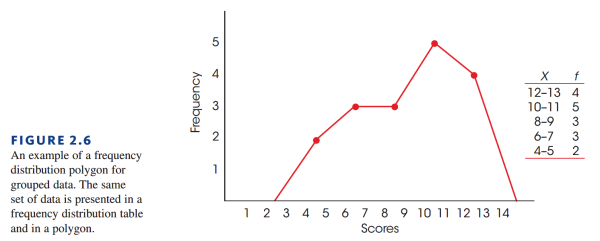
如果是分组频率分布,那么频数所对应的点的 $X$ 坐标应处于组的正中间。比如数据区间为 [8,9],那么点对应的 $X$ 坐标为 $8.5$。
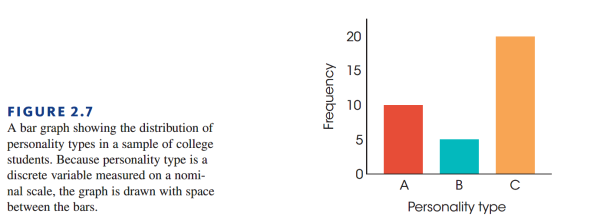
Bar Graphs
Graphs for Population Distributions
之前例子中,我们绘制的图都具有准确的频数数据。但有时候因为数据在不断变化,或者数量太大导致无法准确的计算,我们就需要通过另外一种途径来表示这样的数据了。通常用于表示这种具有模糊性质的数据的图标有两种:相对频数(Relative frequency)与平滑曲线(Smooth Curves)。
Relative frequency
相对频数通常适用于总数非常大的总体。比如我们要评估整个美国中男女的数量,我们就很难得到绝对准确的男女数量。因此,相比拿到具体的男女的人口数量,我们通过大致的数量来制作一张反映相对关系的图:

注意上图的 $Y$ 轴并没有明确的频数。但我们从整个图中也能得到美国人口中男女比例的相对关系。
Smooth Curves
The Shape of a Frequency Distribution
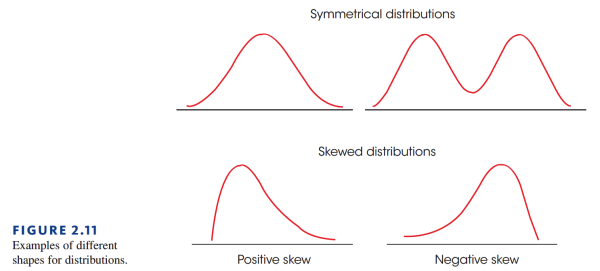
在光滑曲线中,有着很多种不同形状的曲线,而通常我们用分布来命名这些不同形状的曲线。上图就是一个非常有名的分布:正态分布(Normal Distribution)。这个分布由一个公式生成,可以描述自然界内很多现象中的关系。
常见的分布可以分为两类:
- 对称分布(Symmetrical distribution):分布相对于某条纵轴线对称。正态分布就是对称分布的一个很好的例子。
- 偏态分布(Skewed distribution)数据倾向于集中在一边,另一边则留下一条分布尾巴(Tail of the distribution)。数据集中在左边(尾巴偏右)称为正偏态分布(Positive skewed distribution),反之称为负偏态分布(Negative skewed distribution)。
Percentiles, Percentile Ranks, and Interpolation
有时候,一个单独的分数并没有给我们带来足够的信息。比如,你知道了一个人的考试分数 $X$,但你并不知道他在全班的排名是如何的,也不知道比他分低的有多少人。因此,我们考虑对分数处理一下,使其能表示该分数在频数表中的相对位置。通过该处理我们可以得到两个新概念:
- Percentile rank(百分等级):某分数的百分等级指的是在总体中不高于某分数的个体所占总体的百分比。
- Percentile:百分等级对应的分数所处的位置
比如某同学考了 43 分,如果他的百分等级为 60,那么他的百分位数为第60位(60th)。
Cumulative Frequency and Cumulative Percentage
为了求得百分等级,我们需要做一些准备工作。
第一步工作是找出有多少个体处于百分等级对应分数的位置以及其下方。该总数只需要将目标分数下方的所有频数相加即可等到结果。因为结果是累加频数得来,因此我们将该结果成为累积频数(Cumulative frequency),记做 $cf$。
接下来我们将累积频数除以总体个数 $N$,我们就能得到处于目标分数位置以及其下方的所有分数在总体中占的百分比。我们将其称为累积频率(Cumulative percentage)。这是一个更直观的,反映目标分数在个体中位置的指标。我们将其记做 $\%C$,那么很显然有如下的关系:
$$c \% = \frac{cf}{N} (100\%)$$
下面的频数表是累积频数和累积频率的一个例子:
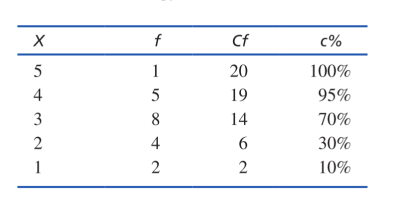
需要特别注意的是,当我们
参考资料
- 本系列笔记所有图片来自于本书中图例。