这是本文档旧的修订版!
Binary Trees, Heaps, SkipLists and HashMaps
−目录
Gtx CS1332x II Notes
BST Introduction
Trees
树(Tree) 是一种链式,非线性的数据结构。在树中:
- 每个节点都有自己的父节点(子节点):
- 每个节点最多只有一个父节点
- 每个节点可能拥有多个子节点
- 没有父节点的节点是树的起点,被称为 root
- 没有子节点的节点是树的末梢,被称为 leaf
- leaf 被称为外部节点(External Nodes)
- 所有非 leaf 的节点被称为内部节点(Interal Nodes)
- 普通列表项目树中遍历的顺序是自上而下的,链接是单向的,不存在从子节点往上开始的遍历。
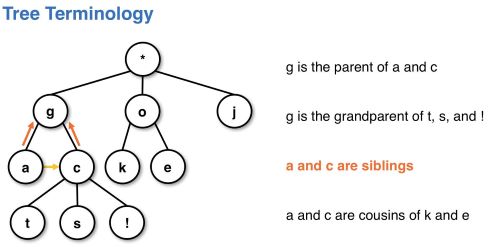
树中的一些术语示例:
- Relationship
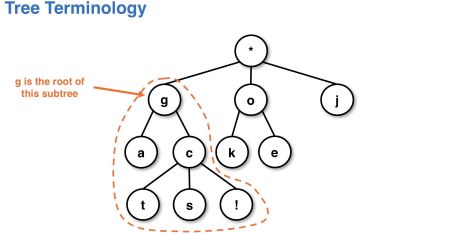
- subtree(Tree 是典型的递归数据结构)
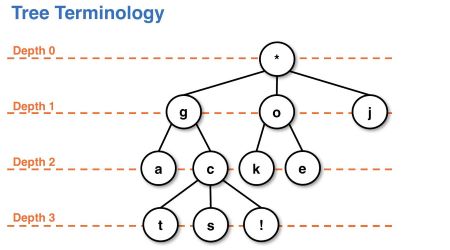
- Depth:节点到 root 的距离。
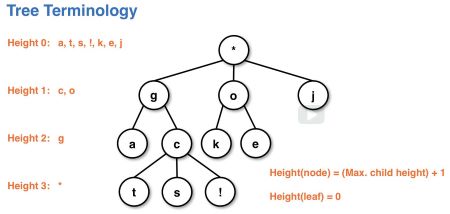
- Height:当前节点最远的 leaf 到当前节点的距离。leaf 所在处 height 为 0
树的特点
- 不是循环结构
- 树是 ADT,具体实现的方法取决于树的类型(多数为链表)
- 树的类型由以下两点决定:
- Shape:节点的结构是什么样子的?
- Order:数据在树中是如何组织的?
- 主要分类:二叉树(Binary trees), 2,4 trees
Binary Trees
二叉树的三个特点:
- 每个父节点最多只能有两个子节点
- 子节点从左到右标记
- 左边的子节点比右边的子节点优先
其节点的组成部分为:
- 指向父节点的引用
- depth
- height
Binary Tree 的形状分类
- Full Tree:除了 leaf 所有的节点都有两个子节点
- Complete Tree:除了 leaf 层,其他层都被填满的树。对于 leaf 层,至少左边要有节点。
- Degenerate Tree:除了 leaf,所有的节点都只有一个子节点。(worst case)
二叉树的遍历
Binarey Search Tree
BST 是 二叉树的一种。除此之外,BST 中内容都是有序的。排序的规则是:左子节点 < 父节点 < 右子节点。这个规则包含了子节点下面的所有子节点。比如下面的二叉树就不是一个有效的二叉树:
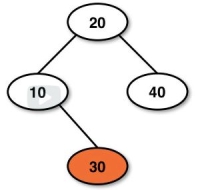
虽然右子节点 30 大于其父节点 10 满足定义,但对于其组父节点 20 来说,30 算作左子节点,不满足左子节点小于父节点的规定,因此该树不是有效的 BST。
BST in JAVA
- 由于 BST 是有序的数据结构,因此需要实现 Comparable 接口用于排序
- 通常,BST 的搜索复杂度为 ,因为在搜索的过程中每次都能筛掉一半的候选条件(类似二分查找)。
- 当树的形状不同时,算法复杂度也不同:
- 当 BST 为 filled 或是 complete 的形态,搜索复杂度为
- Degererate tree (链表) 要求 的搜索时间
- BST 不中存储重复的数据
搜索的方式
- 深度优先遍历(Depth Traversal):使用 stack 实现,对某个分支探索到底之后再返回探索另外的分支。分为 preorder / inorder / Postorder 三种方式
- 广度优先遍历 (Breadth Traversal):使用 queue 实现,对 BST 中的内容以 depth 单位,按层搜索(levelorder)
- 个元素可以组成的 BST 种类等于其卡特兰数(Catalan Numbers),公式为
- 个元素可以组成的二叉树种类等于 乘以其卡特兰数。
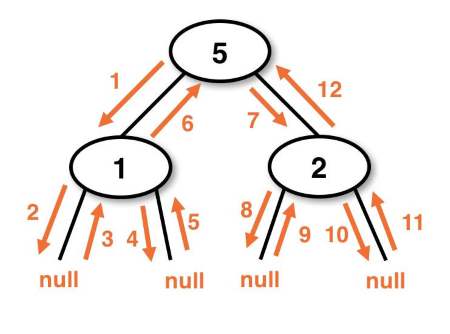
Tree Traversals
- 树中使用递归作为深度遍历的手段。根据读取当前节点内容的时机不同,深度遍历分为三种情况:preorder, postorder, inorder。
Depth Traversals: Preorder
Preorder 会首先进行节点的操作,再进行递归
Depth Traversals: Postorder
- PostOrder 会在递归完毕之后再进行节点的操作
Depth Traversals: Inoder
- Inoder 会先进行左子节点的递归,然后再进行数据的操作,然后再进行右节点数据的递归
Breadth (Iterative) Traversals
广度优先遍历 Breadth Traversals,又被称为 Levelorder,指以树中节点的层级来进行遍历。遍历从 0 层 的 root 开始,每行从左到右依次遍历,是一种很符合直觉的遍历。
实现上,Breadth Traversals 需要额外借助一个 Queue 来实现。其基本的原理为:
- dequeue 父节点
- enqueue 该父节点的所有 children
也就是每次父节点读取完毕时,都会将其清除出队列,将其子节点加入队列。如果父节点同层有其他节点,那么会接着处理其他同层节点。这样保证了父节点所有同层的节点处理完毕之后,才会接着进行下一层的遍历。
BST Operations
Searching in a BST
- 将 root 与目标相比
- 如果目标小于 root,搜索目标的左子节点
- 如果目标小于 root,搜索目标的右子节点
BST 的平均 & 最好 & 最坏复杂度
- 最好复杂度:通常通过对我们最有利的 case 来分析 (通常是单次操作)。比如一个空的 BST,是否能找到匹配结果的复杂度为
- 平均复杂度:BST 的搜索中,平均复杂度基于 amortized analysis, 也就是统计学中的随机变量的期望(exceptation)确定下来的。该类复杂度也被称为 expected preformance。
- 对多种结构(的树)进行同样的操作
- 基于的是所有形状的树的结果
- 假设的是每种树在实际应用中出现的概率都是均等的(uniform Distributed, Unweighted)
BST 的复杂度:
- 平均搜索复杂度
- worst case:degenerated tree,
Adding to a BST
Adding 的实现:Pointer Reinforcement
Adding 使用 Pointer Reinforcement 的策略:
- 通过递归函数的返回值来构建结果树:
- 如果遍历方向为左,则返回左子节点
- 如果遍历方向为右,则返回右子节点
- 构建的手段通过设置 pointer 来实现
Adding 的实现:细节
- wrapper method:对外接口 & where reinforcement happens
- implementation & helper
Adding 的边界条件
- look-ahead:parent 节点(要遍历的节点)为 null
- point-reinforcement:当前节点为 null
Removing from a BST
从二叉搜索树中移除元素需要考虑三种情况:
- 被移除的节点没有子节点
- 被移除的节点有一个子节点
- 被移除的节点有两个子节点
原理:无子节点 & 单子节点的情况
这两种情况比较容易处理:
- 无子节点的情况:移除只需要将被移除节点的父节点对的指向设置为 null
- 单子节点的情况:移除只需要将被移除节点的父节点对其的指向设置为其子节点
原理:双子节点的情况
这种情况需要详细的讨论。首先要明确的是,移除节点不能破坏 BST 的结构。也就是说,节点移除之后,BST 中节点的顺序性依然需要存在。因此,有必要思考通过什么样的手段来维持这种顺序性。
解决方案是使用 Predecessor 或者 Successor。
- 什么是 Predecessor 和 Successor?
Predecessor(最大前继) 是指在 BST 中,比 root 小的节点中最大的一个节点;而 Successor(最大后继) 是指在 BST 中,比 root 大的节点中最小的一个节点。比如下面 BST 中的 21 和 30 就是 root 24 的最大前继和最小后继:
- 为什么要使用 Predecessor 和 Successor?该如何使用?
这种解决方案来源于一种很朴素的想法,化繁为简。首先可以明确的是,直接删除拥有两个子节点的节点,并且还要保证 BST 的结构不出问题,是非常困难的。但相比之下,删除只有一个子节点或者没有子节点的节点则非常简单。因此,相比直接删除节点,我们选择替换节点中的内容,而这正是使用 Predecessor 或 Successor 的精妙之处。
首先,如果希望替换掉 root,那么新的 root 的值必须符合 BST 的规则。也就是说,该 root 必须大于其左树所有节点,并小于其右树的所有节点。root 的 Predecessor 和 Successor 都满足该要求,而且是最符合直觉的两个选择。
其次,来关注一下 Predecessor 和 Successor 所处的位置。由于 Predecessor 大于所有左树中的节点,按照 BST 的排序方法,其只能处于左树的最右端。也就是说,该节点不能拥有右子节点,否则它就不是最大的那一个了。因此可以确认, Predecessor 所在的节点,只可能有两种情况:存在一个左子节点,或者本身就是 leaf。同理,Successor 处于右树的最左边,因此其只能拥有一个右子节点,或者其本身就是 leaf。
Predecessor 和 Successor 这两个特性使得我们可以将删除带两个孩子的节点的操作转变为删除单子节点 / Leaf 的操作。具体的步骤:
- 选择 Predecessor 或者 Successor 作为新的 root
- 交换 Predecessor 或者 Successor 与当前 root 中的值
- 此时需要移除的值已经存在于 Predecessor 或者 Successor 的位置,将其移除即可
实现 1:wrapper
本实现依然使用 point reinforcement 来重建 BST。不过相较于 adding, wrapper 还需要返回被删除的数据:
由于删除节点需要搜许是否存在该节点,因此需要如下的递归搜寻操作:实现 2:found cases
这一部分是实现之前 else 部分中的内容,也就是当存在被删除的内容时,应该如何去执行。我们按照之前的三种情况来实现:
实现 3:helper method for successor
这一部分讨论 removeSucessor 的实现。该方法的功能有两点:
- 搜索 successor
- 将 root 的值进行缓存,并返回当前 successor 的右子节点
SkipLists
SkipList 是链表的一个变种。与链表不同,SkipList 是一种随机(基于概率的)数据结构。Skiplist 的主要优势是将链表中元素搜寻的平均复杂度从 降低到了 。
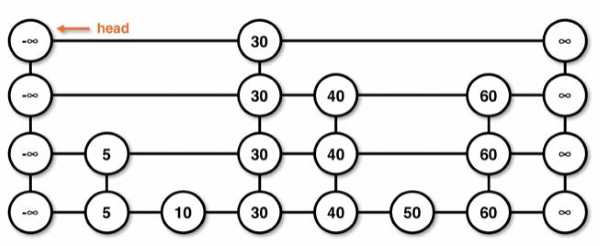
Skiplist 的结构
Skiplist 的构建
我们通过投掷硬币(Coin Toss)的方法来决定更高层的链表的元素为哪些。每添加一个元素,我们投掷一次硬币。如果掷出的硬币是正面(head),那么该元素就会被提升(poromote)到下一层;如果结果是反面(tail),则结束操作。之前我们提到过,理想状态下上层元素应该为下层元素的一半;这也很符合投硬币概率的直觉。
这样的创建方式使 skiplist 具有两个明显的特征:
- 最底层的链表一定包含了所有元素
- 上层的链表中,每个元素与其正下方的元素一定等同。
Skiplist 的不同层级可以想象成起始点一样,终点一样,但停站不一样的公交路线:
- 底层可以想象为每站都要停的公交车
- 上层可以想象为只停其中某些站的快速公交车
需要注意的是,skiplist 中存在负/正 无穷的边界。实现上,该边界被称为 Phamtom nodes,用于作为 skiplist 的起始和终止的标记。
Skiplist 的搜索原理
搜索的算法如下:
- 从左上角的 phamtom node (head)开始
- 比较当前 data 是否与同层右边的数据
- 如果大于,则移动查找位置到当前比较的节点,并继续往右边查找
- 如果小于或是本层元素已经比较完毕,则往下层进行查找
- 重复以上的处理,直到达到最底层
Adding in Skiplist
- Skiplist 的元素添加是根据硬币投掷的结果来决定的。如果按照从下到上的添加方式,那么
T则代表只在0层添加元素;HT代表在0-1两层添加元素,依次类推。 - 添加中需要判断插入元素的位置,因此需要结合搜索和添加使用。元素都会被插入到第一个大于自身的元素之前
- 添加元素需要判断是否存在该元素。可以先搜索是否存在该元素,如果不存在则以 coin toss 序列的结果添加该元素到各层。
Removing in Skiplist
- 搜索元素
- 如果元素不存在,则返回 Null
- 否则,以第一次搜索到的层级位置为基础,自上往下移除所有该元素。
Heaps
Heap(本课讨论的是 Binary Heap) 的本质是二叉完成树(Complete Tree)
- 由于完成树没有节点的间隙,因此 Heap 可以轻易使用数组实现
- 排序使用 levelorder
与 BST 不同的是,Heap 只对父节点和子节点的大小有要求(对 sibling 没有限制)。根据子节点与父节点的大小关系,Heap 分为:
- MinHeap:root 为最小值的 heap
- MaxHeap:root 为最大值的 heap
由于 Heap 的最大(最小)元素处于 root 的位置,我们通常使用其作为 Priority Queue 的实现基础。Heap 不是搜索型数据结构,在 Heap 中的元素查找复杂度为 。
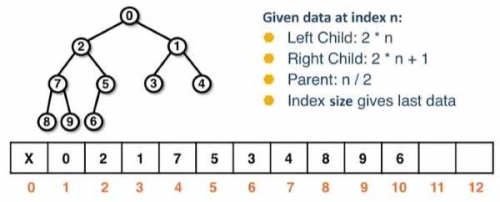
Heap 在 Array 中的表现
Heap 使用 1-indexed 的方式来决定下标,即 index 0 不存储任何值。配合 levelorder 的排序方式,假设当前节点的 index 为 ,可以得到如下几个性质:
- 其左子节点的 index 为
- 其右子节点的 index 为
- 其父节点的 index 为 (整数除法,因此左右子节点都可以得到同样的结果)
- 其最后一个节点的 index 为
size(而不是 size - 1)
Heap Operations
根据 Heap 的定义,Heap 的操作通常包括添加与删除。操作过程需要遵循如下的两个要求:
- 优先保证结构不会破坏。也就是操作完成之后,得到的结果也必须是完全树
- 其次保证节点的顺序性。在保证结构时候,根据顺序性的要求需要交换节点的位置
这两个要求决定了 Heap 的添加与删除的特性:
- 添加的节点永远都是在 leaf 层的最右边一个节点
- 删除的节点内容永远都是 root 的内容,删除的位置是 leaf 层最后一个节点。因此,删除需要将 root 与 leaf 层最后一个节点的内容进行交换
Adding in heap
Adding 的操作分两个步骤:
- 保证结构的完整性:添加元素到 leaf 层的最右边一个位置
- 保证顺序的正确性:将添加的元素与其父节点比较,如果顺序不符则进行 swap(该过程被称为 up-heap 或 heapify)
Remove in heap
Remove 的操作也分两个步骤:
- 保证结构的完整性:移除 root 处的元素,但实际上移除的是 heap 中最后一个元素(right-most element in leaf level)
- 将最后一个元素的内容替换到 root 所在节点中,并移除最后一个元素
- 保证结构的顺序性:
- 如果当前节点有两个子节点,则比较当前的两个 children,选取优先级较高的与 root 中的内容比较
- 如果当前节点有一个子节点,则直接进行比较
- 如果比较结果不符合正确的顺序,则进行 swap,一直到 leaf level 结束(not children)(该过程被称为 down-heap)
Up-heap 和 Down-heap 的复杂度均为
The BuildHeap Algorithm
如果已知一个数组,希望将其生成 Heap 的话,有两种办法:
- 从头开始往里添加元素,每次 add 操作的复杂度为 ,因此总操作的复杂度为
- 使用 Down-heap 的方式重建 heap,复杂度为
Down-heap 的生成原理和方式
Down-heap 的方式是指,从 heap 中末尾的元素所在子树开始重建;子树重建完毕之后,再基于该结果进行更大的子树重建,直到整个数组中的元素用完为止。这样做的好处是,Down-heap 的规模不会超过当前子树的规模。这样使得 down-heap 生成 heap 的方式的复杂度不会超过 。
按上述的思路,重建的父节点的遍历起始点是 size / 2,因为最后一个节点的 index 为 size。因此可以确认:
- 遍历的范围为
[size / 2, 1] - 每遍历一个父节点,则对该节点进行 Down-heap
- 直到父节点遍历到 root 并完成 down-heap 时,整个 heap 建立完成。
HashMaps
Maps
Map 是一种非顺序的数据结构。其元素由 Key 和与其绑定的 Value 组成。其中:
- Key 是唯一的,不可修改的(Immutiable)
- Value 不唯一,可以设置为修改或者不可修改
Map 的常见方法
put(<K, V>):根据关键字进行值的修改;如果关键字不存在则添加get(K):根据关键字取回值V remove(K):根据关键字移除元素,并返回对应的 valuesize():查询 Map 中由多少元素
HashMap
HashMap 是 Map 的一种。这种数据结构是基于数组实现的,并将数组中的元素(Key)与特定的数进行绑定,从而达到 查找的效果。该特定的数通过特定的 Hash Function 生成,其被称为 Hash Code。
HashCode Collision
Hash Code 有一个很重要的特性:
- 如果两个 Key
equal,那么这两个 key 的 Hash Code 相同 - 但两个相同的 Hash Code 并不能推断出两个 Key
equal
这是因为,理想状态下,HashCode 应该与 Key 一对一的关联。但实际上,这样的操作会造成大量的资源浪费。假设我们学院下存在 6 个部门,每个部门有一个 10 位长度的电话。理想情况下,我们应该使用电话号码作为与部门绑定的 Hash Code。但这样做相当于使用了 10 位长度的数组(组合为 10^9)的 Hash Code, 来表示仅仅 6 个 Key,这完全是得不偿失的。这也是为什么我们需要使用 Hash Function:尽量的使用最少的资源来绑定所有的 Key。
以上面的电话为例,一种可行的 Hash function 是,取电话的后 4 位来作为 Hash Code。这样之后,单个 Hashcode 的长度从 10 位变为了 4 位。当然,我们还可以做进一步的优化,比如将 4 位的 HashCode 末除 100,最后得到的结果只需要 2 位的数组就可以表示。这种进一步的优化过程被称为 Hash Compression。
不过,在上述的过程中,就可能会导致相同的 HashCode 指向不同的 Key。比如有两个电话:4048942261 / 4048940961。经过上述的第一步筛选后,其对应 HashCode 为 2261 / 0961;但再通过第二轮筛选后,结果都变成了 61。这种情况被称为 Hash Collision。通常情况下,这种情况是不可避免的。
减少 Hash Collsion 的策略
由于 Hash 的过程缩小了原有 Key 绑定的可选择范围,为了尽量避免出现 Hash Collision,最好的策略是对 Hash Code 数组的可选范围进行控制。一般来说,当出现了 Hash Coolsion 时,我们可以:
- 使用新的,较大的 table 来作为新的选择范围,一般新范围是
capcity * 2 + 1 - 根据 loading factor 来 resize table 的大小:
- loading factor 指 hash code 的占用率:
size / capcity - 通常这个数应该控制在 之间
从设计上避免 Hash Collision
Hash Function 的选择在设计 Hashmap 中至关重要。一个好的 Hash Function 可以阻止 Hash Collision 的发生。
以 String Key 为例子:
- 首先需要考虑的是如何将 Key 转换为 Hash Code。一种方法是按照字母的顺序将其与自然数对应,比如
A对应1,B对应2,而整个字符串可以表示为所有数之和,比如ABAB就是1+2+1+2 = 6。 - 其次应该观察 Hash Function 是否完整保留了所有的信息。本例下可以发现,
6只体现出了有哪些字母,而并未说明字母按什么顺序排列。因此,我们可以使用带权数对其进行表示。比如将字母的位置以10的指数来表示:
其他设计中的重点
首先,设计 hash function 必须满足两个条件:
- 转换结果为 integer
- 转换后,若 Key 值相同,那么对应的 hash code 必须相同
其次,需要考虑 compression function 的设计:
- 一般使用
mod capcitity的方式来实现 - 这种方式可以保证 compreesion 的结果是平均分布的(evenly distribute),这样可以更好减少 Collsion 的发生
- table size 尽量选取质数(primer numbers),这样可以有效的防止 Collsion 的放生
- table size 也可以选用 2 的幂(相较于末除,使用 Bitmask 可以有效的提高 compression 的效率)
最后,考虑 loading factror。loading factor 越低,出现 Collision 的几率就越低,但带来的资源消耗就越高。
External Caining
External Chaining 是处理 Collision 的一种方式。当 Entries 的 index 相同( Hashcode 相同或是 compreesion 的结果相同)时:
- 将该 index 代表的 entry 视作一个起点创建一条链表
- 满足条件(当前 index)的元素则插入到该链表的头部(也可以是尾部,根据实现方式)
Resizing
使用 External Chaining 管理 Collision 时,由于使用链表来存储 Index 相同的元素,在 Hash function 不是很好的情况下,有时候会导致某一个 index 下的链表特别长。链表的查询效率为 ,因此我们需要在链表的长度达到一定的情况下进行 resize,来重新排列已经存储的元素。
实现上,是否 Resizing 也根据 Loading Factor 来决定。但 External Chaining 管理的 Hashmap 中,Size 不是单指 Backing array 中所占用的空间,而是要把所有的元素都计算进去。比如整个 Backing Array 的 Capacity 是 10,Backing Array 中只有 0 位置被占用了,但 index 0 下有 5 个元素,那么该 Hashmap 的 Loading Factor 就是 5 / 10 = 50%。可以看出来,External CHaining 下的 Hashmap, Loading Factor 是可以大于 1 的。
这种类型的 Hashmap, 其 Resizing 的过程是希望重新按新的 index 进行元素的分配,通过减少 Collision 链表的长度来达到更好的查询效率,而不是像 Vector 一样翻倍空间再拷贝。因此,Hashmap 的 Resizing 不涉及元素的拷贝,而是对原有的每个 index 下 所有 的元素,使用其 Hashcode % new BackingArray.length 来进行重新排列。
Linear Probing
与 Extenral Chaining 将元素锁定在对应的 Index 不同,Probing 是一种 Open addressing 的策略。Probing 在处理 Collision 的过程中,会按相应的策略将元素置于 backing Array 的其他位置。Linear Probing 指采用了如下策略的 Probing :
put() in Linear Probing
- 如果在某个 index 处出现 Collision,那么将当前 index 加一
- 如果 backing array 的下一个位置有空,则存储元素于该处
- 否则,继续将 index 加一,直到找到空位
查询空位(index 自增)的过程是一个循环的过程。最坏情况下,查询会进行 次(如果元素为 个)。如果起点不是 index 0,那么当查询达到 backing array 的末尾时,需要回滚到数组的前段继续进行查找。因此,如果令 为当前递增的步数,那么 当前递增后的 index 的计算方式为:
remove() in Linear Probing
移除 Hashmap 中的元素与 put() 的操作类似:
- 根据初始的 Index 计算 probe 的起始位置
- 将当前元素于需要被删除的元素相比
- 如果是,则删除
- 如果不是,则递增当前 Index 进行下一个位置的比较
但上述的步骤存在一个问题:假设存在多次 remove 的操作,如果第一次删除的位置处于第二次删除的位置之前,那么第二次的 probing 会在第一次删除的位置处中断,因为此处为空,已经没有元素可以进行相比。
为了解决这个问题,probing 的删除采用了软删除(sofe removal)的方式来实现。当删除一个元素时,我们会在其位置填充一个 DEL Marker,来体现此处曾经有元素存在,从而来保证 probing 的过程不被中断。
DEL marker 会给 put() 带来一些变化。假设我们向带有 DEL marker 的 hashmap 中添加元素,如果该元素在 DEL marker 之前都没有位置可以放置,那么该元素将存放于其遇到的第一个 DEL marker 处。
resizing with DEL markers
DEL marker 会带来一个性能上的缺点:其占据 probing 的位置,但又不会影响 loading factor。可以考虑这样一种特例:数组中只有最后一个元素存在,其前面所有的空位都被 DEL marker 填充。这导致了无论是什么样的操作,都必须遍历完整个 backing array ()。因此,当 resizing 的时候,任何之前 hashmap 中 DEL marker 都会被舍弃掉,不参与 rehash。
DEL marker 应该被考虑到 loading factor 中,且应该设置一个 removal 的上限来触发 resizing。
Quadratic Probing
Linear Probing 带来的问题被称为 primary clustering(turtling)。该问题指当 hash map 中连续的区域越来越大时(这是必然的,因为递增找空最终会将整个 hashmap 变为连续的区块。),我们每做一次 Probing 找空位都要跨越之前的连续区块。因此,我们需要一种更快的方式来找空位。
一种方式是将之前计算 index 中的 (h + oriIndex) % backArray.length 更改为:
Preformance
SkipList
| Best Case | Average Case | Worst Case | |
|---|---|---|---|
| Search | |||
| Add | |||
| Remove | |||
| Space |
Heap
| Operation | Best | Average | Worst |
|---|---|---|---|
| Find Min / max | |||
| Add | |||
| Remove Min/max | |||
| Aribitray Search/Remove | |||
| BuildHeap | - | ||
| Space Complexity |