目录
Cartesian Coordinate Systems
3D math primer chapter 1
1D Mathematics
- 自然数(natural numbers) 起源于计数,可以描述为数轴(number line)的形式。
- 整数(interger)包含正(自然数)和负数。
- 分数(fractional number)作为整数的补充,填满数轴。小数(decimal)作为分数的一种书写形式存在。
- 实数(real numbers)如果以分数的形式表示,需要无限的小数位。因此,实数是不可计量的。
- 研究有限数的数学称为离散数学(discrete mathmatics),研究实数的数学称为连续数学 (continuous mathmatics)。
- 图形学 / 计算机使用有限的数字来描述CG。无论是什么类型的数据,最后都将用有限的形式表现,唯一不同的是精度。
If it looks right, it is right. - The First Law of Computer Graphics.
2D Cartesian Spcce
2D 笛卡尔空间 (Cartesian Space) 是一种使用坐标系描述平面的空间。其主要的概念包含:
- 原点(The Origin)
- X / Y 轴 (x- and y axes)
- 轴的方向
Arbitrary 2D Coordinate Spaces
任意 2D 笛卡尔空间有两个特性:
- 每个 2D 笛卡尔空间都拥有原点(origin),该位置为整个空间的中心。
- 该空间拥有两条无限长的、穿过原点的、并互相垂直的直线。
这两条直线被称为 x轴 (x-axis,从左到右)、y轴(y-axis,从下到上)。但需要注意的是,坐标轴的朝向是可以任意变换的;我们唯一要提前声明的是坐标轴的正负 与轴方向的关系。这是因为无论我们为坐标轴选择了什么样的方向,我们都可以通过旋转对应的坐标空间来达到一种约定俗成的坐标轴方向(y从下往上,x从左到右),换句话说,旋转(rotate)不会扭曲原有空间。
Specifying locations in 2D
坐标空间实际上是为了精确的定位而建立的框架。在 2D 空间中,通过一对数字(两个坐标)即可精准的指定任意该空间内位置。这一对有序的数字被称为笛卡尔坐标(Cartesian coordinates)。该对数字分别描述 x 和 y 轴上的位置。更精确的来讲,该对数字是有符号的距离(signed distance),用于描述当前位置距离远原点有多远,方向如何。描述的方式是按坐标轴的方向来描述,第一行描述在 x 轴上的位置与原点的距离,第二行描述在 y 轴上与原点的距离。
3D Cartesian Space
3D 笛卡尔空间较 2D 来说,需要讨论额外的几个问题:
- z 轴
- xy, xz 和 yz 平面
- 左手 / 右手 坐标系的判定,在不同坐标系下旋转的区别,以及这两种坐标系中如何相互转化。
Extra Dimension, Extra Axis
3D 空间较 2D 多出了一个坐标轴。像 2D 一样,3D 空间中的坐标轴是两两垂直的。但与 2D 中不同,3D 中,坐标轴的方向与物理中的方向(上下左右等等)的对应关系并没有绝对的标准。同时,在 3D 空间中,任意两条坐标轴组成的平面,必与第三条坐标轴垂直。因此,如果定义了三条坐标轴的物理方向,那么就能确定空间的“地面” 在哪里。
Specifying Locations in 3D
3D 空间中,位置同样以一组有序的,3个数字的 signed distance 来描述。不同于 2D 的是,3D 空间中的距离指的是位置在某条坐标轴上的位置与其垂直的平面的 signed distance。
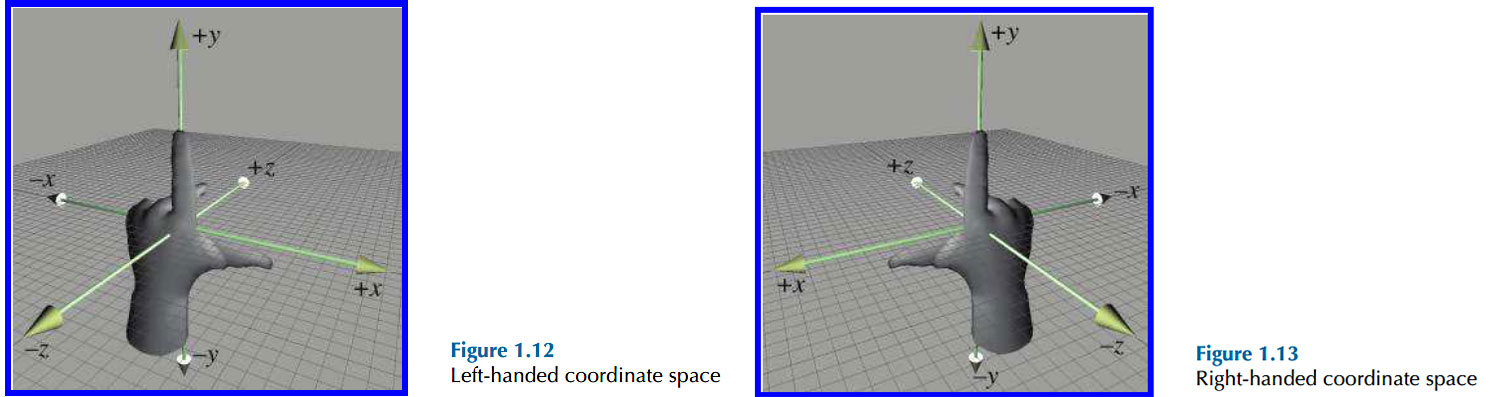
左手 vs 右手
在 2D 空间中,任意空间是等同的。也就是说,无论x,y 如何定义正负,我们都可以将其标准化。这是因为我们可以通过旋转空间来得到标准的正方向(就好像旋转一张地图一样)。
然而在 3D 空间中却不是这样的。不是所有的 3D 空间都是等同的。一个典型例子:如果 z 轴的方向是朝向 xy 平面内部,那么我们是无法通过旋转来得到以下结果的:
- z 轴指向 xy 平面外部
- 新的空间等同于原有空间
因此,z 轴指向xy平面内与指向xy平面外,实际上是两个不同的空间;我们将这两种空间区分为左手空间(Left-hand coordinate space)和右手空间(Right-hand coordinate space)。可以得出结论,如果两个空间有相同的惯用手(Handedness),那么这两个空间是等同的,可以通过旋转来对齐的;反之则不可能。
左手 / 右手 空间的判定规则如下图,大拇指方向位 +x, 食指方向为 +y, 中指方向位 +z:
Positive Rotation
在左手空间与右手空间中,正方向旋转的定义也是是不同的。假设旋转围绕着一条轴(Axis of Rotation),那么如果用大拇指代表旋转轴的正方向,那么在不同的 3D 空间中有着不同的约定俗成的正方向,也就是所谓的左手/右手定理(Left-hand / Right-hand Rule):
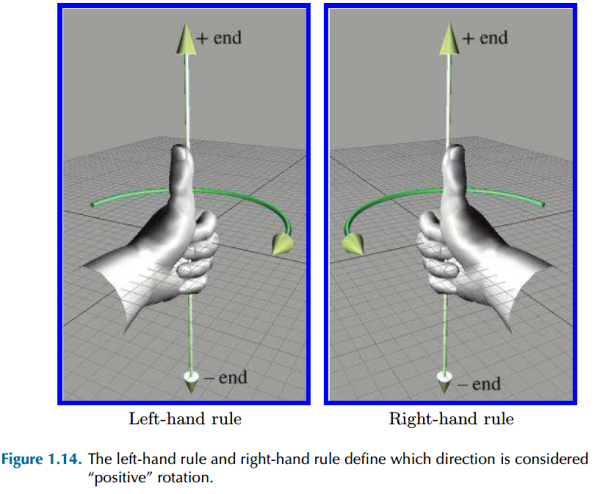 该定理规定所有除开大拇指的手指指向的方向为旋转的正方向。
该定理规定所有除开大拇指的手指指向的方向为旋转的正方向。
旋转轴自身可以为空间内任意的一条轴(自身可以随意旋转),并不一定是 cardinal axis (像 x、y、z一样的轴)
左手 / 右手空间的相互转化
左手空间与右手空间可以进行任意的转化。最简单的方式是直接将某一个坐标轴的正反对调即可。Tips:
- 同时翻转两条轴不会改变惯用手
- 工作前先检查坐标空间的惯用手。如果表现不对,尝试翻转 Z 轴的方向。
本书习俗
- 使用左手空间
- 书中指的 north / east 一般指以地面为二维平面作为衡量标准。
相关的基础数学
- 和/积的符号(sum / Product notation)
- 区间符号
- angle、Degrees、Radians
- 三角函数
术语
- Handedness: 惯用手
- Revolution: 用于描述一整圈(360 dregee / 2pi radian)
- isosceles / right triangle: 等腰 / 直角三角形