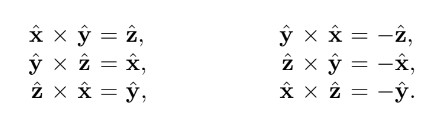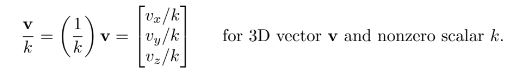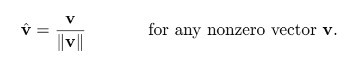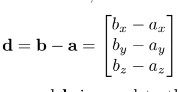目录
Vectors
3D math primer chapter 2
Vector 在数学上和物理上有不同的解释。数学上强调向量是一组数字,物理上强调向量是一个几何实体,并在尽可能的避免用坐标系去表述向量。
向量的数学定义
数学 / 计算机上来说,Vector 等同于 an array of numbers.
一些常识
- Scalar: 标量,强调不是矢量
- Dimension: 指向量包含了多少数字。
- 向量有行/列写法。通常写成列向量(column vector),也就是按从上到下的方式写。
- 指定向量的某个元素:通过下标(subscript notation)来指定。通常在2、3、4维向量中(图形学),可以使用 x、y、z、w 代替数字下标。
C++中变量的命名一般采用与3D数学中对应的符号:
- Scalar 使用小写罗马字母:$a,b,x,y,z,\theta,\alpha$ 等等。
- Vector 使用粗体的小写字母: a, b, u, v, q, r。
- Matrix 使用大写粗体字母 A, B, M, R。
- 向量一般用头顶箭头表示 $\vec\alpha$。
线性代数与3D数学
3D数学主要考虑的是向量的几何解释与向量的操作。除少数要讨论n维矩阵的特殊场景,绝大大部分情况下只会用到2D、3D、4D的向量和矩阵。
向量的几何定义
几何上来说,向量是具有 大小(magnitude)和方向(direction)的线段。向量具有头部(head)和尾部(Tail)。从尾部到头部的方向即为向量的方向。
向量没有位置
向量本身没有位置,只有大小和方向,通常用于描述事物之间的相对关系:比如 velocity 和 displacement(可对应标量的 speed 和 distance)。因此,只要大小方向一致,我们可以在任意位置描述同一个向量。
向量与笛卡尔坐标系
向量是一系列的位移
向量可以描述成一系列的累积位移而得到的最终结果;位移的顺序不重要。
零向量
零向量是一个特殊的向量,该向量的维度与空间相同,向量中每一个分量的大小都为 0。相比其他向量,零向量有两个特点:
- 大小为 0
- 没有方向
零向量满足 additive identity (也就是 $\vec{a} + \vec{0} = \vec{a}$)
零向量的描述
在示意图中一般将零向量描述为点(此处的点绝不意味着位置)。
Vectors v.s. Points
通过之前的内容可以得出的结论是:向量强调的是位移的大小与方向,点强调的是位置。但实际上这两者是具有联系的。
Relative Position
需要明确的是,绝对的位置是不存在的。任何有意义的位置描述,必须基于一个原点来描述其位置。因此,对于位置的描述,都可以视作相较于原点的相对位置。更准确的说,位置是基于某种描述框架下的相对位置。
同时,相对位置可以使用位移来描述。比如某一个位置可以描述为“从原点开始,往上移动多少,往左移动多少”。在指定的框架中,向量用于描述从原点开始的位移,而点用于描述通过该位移得到的,相对于原点的位置,因此这两者之间是可以联系起来的,也就是在数学上是等价的。
任意的点都可以表示从原点出发的向量。
Vector Operations
Negating
Negation operation 也适用于向量,如下: $$\vec{v} + (\vec{-v}) = 0$$ 当 Negating 向量的时候,需要将向量中每一个元素进行反转。
Negating 的几何解释
Negating 得到的结果是一个 magnitude 相同,但 direction 完全与原向量相反的新向量。
Vector * Scalar
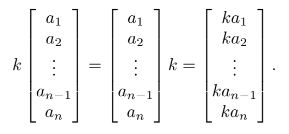
Vector * Scalar 的几何解释
向量与标量的乘法在几何上等于将向量按标量倍数缩放。
Vector 的加减法
数学上来说,当对 vector 进行加减的时候,实际上是对 vector 中的对应元素进行加减:
 加法满足交换律(Communitive),而减法满足反交换律(Anti-Cimmunitive,$a-b = -(b-a)$ )
加法满足交换律(Communitive),而减法满足反交换律(Anti-Cimmunitive,$a-b = -(b-a)$ )
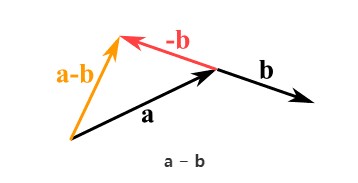
加减法的几何解释
$b$ 以 $a$ 的头部作为起始点。结果为以 $a$ 的尾部为起点,$b$ 的头部为终点的新向量。显然先 $a$ 后 $b$ 的结果与 $a+b$ 的结果相同,这也被称为向量加法的三角形法则。减法也同理:
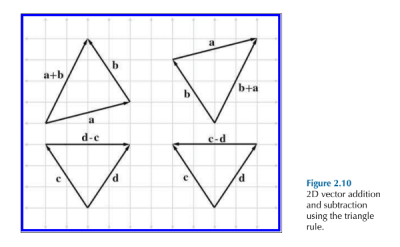
注意上图的减法,d-c 与 c-d 得到的是不同的向量。
三角形法则可以被拓展到多个向量的加减法中。从几何上来说,这就是之前提到的一个向量可以被描述为在多个方向上的位移。
三角形法则的一个重要的点就是第二个向量的tail永远是第一个向量的head,而得到的结果始终是从最初的向量的tail到最后向量的head 的连线。根据这个性质可以很简单的推导出减法。
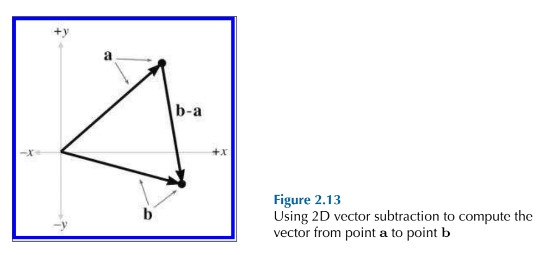
计算两点之间的 displacement
Vector Length
向量的长度又称为向量的 Magnitude, 也被称为向量的范数(norm),其计算方式为分量平方和的平方根:
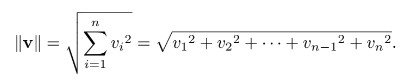
关于这里的 Norm
总的来说,Norm 是指任何满足一系列相关条件的等式。就向量长度而言,应该更精确的被称为 2-Norm,也就是用于测量欧式空间距离的范数。
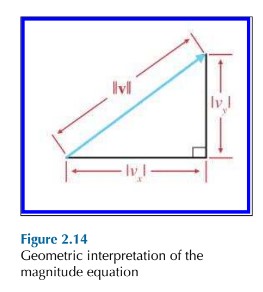
向量长度的几何解释
Unit Vector
单位向量(Unit Vector),又称标准化向量(normalized Vector),用于只考虑向量的方向而不考虑向量的大小的情况下。单位向量的 magnitude 为 1。
单位向量经常也被称为法线 (Normal),但这么做需要有一个前提:法线是垂直于某某的单位向量。比如 surface normal 就是垂直于当前表面的法线。需要注意的是,这里的 Normal 指代垂直,而不是单位长度。所以:
- Normalized Vector:单位向量
- Normal:单位向量,并垂直于某物
单位向量的计算
几何解释
单位向量的 tail 为原点。在 2D 中单位向量的 head 会达到单位圆,3D 中会达到单位球。
两点距离公式
Dot Product
点乘(Dot Product)是两种向量乘法的一种。点乘将两个向量对应的分量乘在一起,然后把所有的结果累加,最终得到的是一个标量: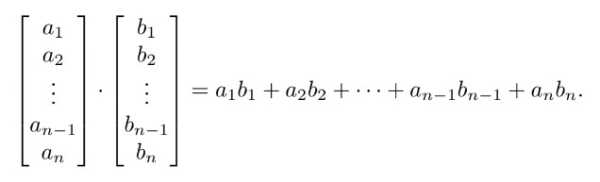 也可以用累积和的方式描述:
$$a \cdot b = \sum_{i=1}^{n}a_{i}b_{i}$$
也可以用累积和的方式描述:
$$a \cdot b = \sum_{i=1}^{n}a_{i}b_{i}$$
点乘的几何解释
第一种几何解释将点乘试做一个向量在另外一个向量方向上的投影(Projection)。假设 $\hat a$ 为单位向量,$b$为任意长度的向量,则 $\hat a \cdot b$ 的几何结果如下图: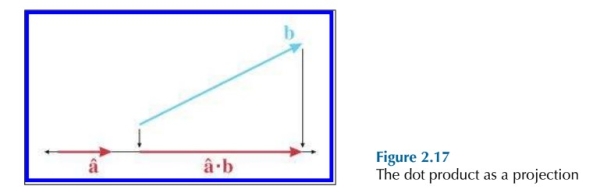 那么实际上,$\hat a \cdot b$ 的结果就可以被定义为 $b$ 在 $\hat a$ 方向上投影的长度。需要注意的是,这里得到的长度是有正负的。当 $b$ 与 $\hat a$ 的方向相反的时候,很显然得到的投影方向也是与 $\hat a$ 相反的。实际上,会出现三种情况:
那么实际上,$\hat a \cdot b$ 的结果就可以被定义为 $b$ 在 $\hat a$ 方向上投影的长度。需要注意的是,这里得到的长度是有正负的。当 $b$ 与 $\hat a$ 的方向相反的时候,很显然得到的投影方向也是与 $\hat a$ 相反的。实际上,会出现三种情况:
- $\hat a$ 与 $b$ 方向相同,点乘结果为正
- $\hat a$ 与 $b$ 方向垂直,点乘结果为 0
- $\hat a$ 与 $b$ 方向相反,点乘结果为负
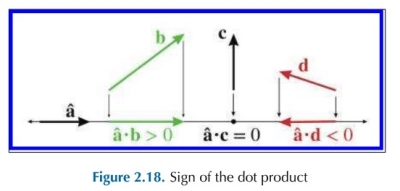 那么很容易推论出,两个向量的点乘结果,实际上在说明这两个向量在方向上的相关性。
那么很容易推论出,两个向量的点乘结果,实际上在说明这两个向量在方向上的相关性。
同时,根据点乘的公式,对 $\hat a$ 或者 $b$ 进行缩放(乘以标量),对投影只会产生相同的缩放效果:
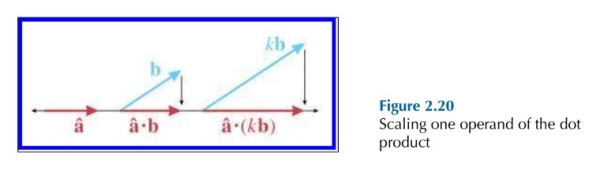 代数上可以表现为:
$$(ka)\cdot b = k(a \cdot b) = a \cdot (kb)$$
因此点乘可以定义为:
代数上可以表现为:
$$(ka)\cdot b = k(a \cdot b) = a \cdot (kb)$$
因此点乘可以定义为:
The dot product $a \cdot b$ is equal to the signed length of the projection of $b$ onto any line parallel to $a$, mulitiplied by the length of $a$.
点乘的性质
- 点乘遵循交换律(Communitive):$a\cdot b = b \cdot a$
- 点乘遵循分配律(Distributes):$a \cdot (b+c) = a \cdot b + a \cdot c$
两个性质都可以通过点乘的代数定义证明。
几何意义上:
对于交换律,$\hat a$ 投影到 $\hat b$ 上与 $\hat b$ 投影到 $\hat a$ 上的向量长度是一致的,因此无论是 $a$ 投影还是 $b$ 投影,本质上都是在对投影的结果做缩放,不影响投影的最终结果。
对于结合律,$b+c$ 可以看做 $b$ 和 $c$ 两个向量的和,而根据下图,$b+c$ 向量的投影长度正好等于向量 $b$ 和 $c$ 投影长度的和:
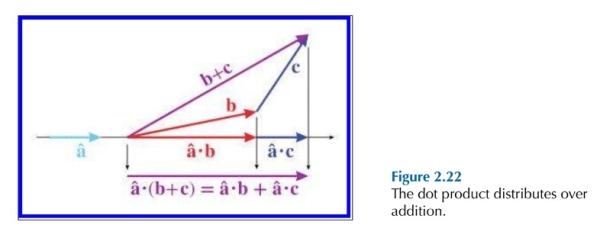
向量自身的点乘等于在 x 上的分量
来看一种特殊情况。假设坐标轴(Cardinal axis)是被投影的对象。举个例子: $\hat x \cdot b$ 。可以发现的是,该点乘的结果实际上就是 $b$ 在 x 轴上的分量的长度:
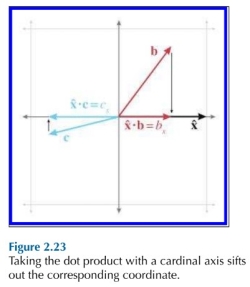 可以看出来的是,点乘结果的方向始终是被投影的向量一致的。而当参与点乘的两个向量方向一致的时候,也就是向量求自身在自身上的投影的时候,我们得到的结果实际上是向量本身的 magnitude,即:$$v \cdot v = ||v||$$
可以看出来的是,点乘结果的方向始终是被投影的向量一致的。而当参与点乘的两个向量方向一致的时候,也就是向量求自身在自身上的投影的时候,我们得到的结果实际上是向量本身的 magnitude,即:$$v \cdot v = ||v||$$
求已知向量的平行/垂直分量
假设有单位向量 $\hat a$,任意长度的向量 $b$,用 perp 表示 $b$ 在竖直上的分量,para 表示 $b$ 在水平上的分量。根据前面提到的推论,则有:
$$b_{para} = \hat a \cdot b = (\hat a \cdot b) \cdot \hat a$$
根据三角形法则:
$$b_{perp} = b - b_{para} = b-(\hat a \cdot b) \cdot \hat a$$
这一小节实际上是在利用点乘的性质来求已知向量的平行/垂直分量。首先利用点乘的结果是被投影(平行)分量的 magnitude 求出平行分量的长度,再与被投影向量的单位向量相乘得到方向,从而得到投影向量在被投影向量上的分量,也就是平行分量。
得到该分量后,因为向量可以通过自身的水平分量和垂直分量相加得到(三角形法则),因此垂直分量只需要用向量减去水平分量即可。
点乘的第二种几何解释
假设有单位向量 $\hat a$ 与 $\hat b$,且夹角为 $\theta$,根据点乘的投影解释,可以构造出一个三角形如下图:
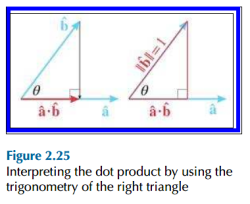 可以得出 $$cos\theta = \frac{adjacent}{hypotenuse} = \frac{\hat a \cdot \hat b}{1} = \hat a \cdot \hat b$$
也就是说,两个单位向量的点乘结果等于这两个向量之间夹角的余弦值。
可以得出 $$cos\theta = \frac{adjacent}{hypotenuse} = \frac{\hat a \cdot \hat b}{1} = \hat a \cdot \hat b$$
也就是说,两个单位向量的点乘结果等于这两个向量之间夹角的余弦值。
现在假设 $a$ 的长度为 a, $b$ 的长度为 b,那么上面的等式可以写成:
$$cos\theta = \frac{a \cdot b}{||a||||b||}$$
因此点乘从角度观点的几何解释可以归纳为:
The dot product of two vectors $a$ and $b$ is equal to the cosine of the angle $\theta$ between the vectors, multiplied by the lengths of the vectors. Stated formally,$$a \cdot b = ||a||||b||cos\theta$$
这种解释下的点乘有几个功能:
首先,可以使用该解释来求出两个向量直接的夹角:$$\theta = arccos(\frac{a \cdot b}{||a||||b||})$$如果不考虑 magnitude,可以直接使用单位向量求该夹角:$$\theta = arccos(\hat a \cdot \hat b)$$
其次,$\theta$ 的值可以用于判断当前两个向量方向的关系:

Cross Product
Linear Algebra Rules
Cross Product(叉乘&内积)记作 $a \times b$。3D 叉乘的代数公式如下:
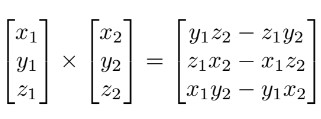 几个重要的代数性质:
几个重要的代数性质:
- 普通列表项目cross product 遵循与 dot product 同样的运算优先级。但在混合点乘与叉乘的计算中,优先计算叉乘,比如 $a\cdot b \times c = a \cdot (b \times c)$ 。
- cross product 不遵循 commutative,遵循 anticommutative,即 $a\times b = - b \times a$
- cross product 也不遵循 associative,比如 $(a\times b)\times c \neq a \times (b \times c)$
优先计算叉乘是为了保证复合计算有意义。如果先进行点乘,那么点乘得到的标量,是无法与向量进行叉乘的。
叉乘的几何解释
Cross product 结果会产生一个新的向量,该向量与参与叉乘的两个向量分别垂直:
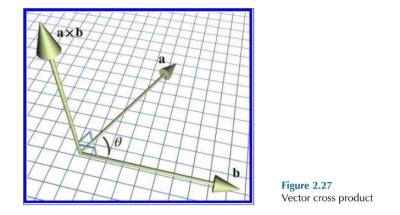 新向量的 magnitude 按如下公式计算:
$$||a \times b||=||a||||b||sin\theta$$
有意思的是,该结果正好等于 a、b 按平行四边形法则形成的四边形的面积:
新向量的 magnitude 按如下公式计算:
$$||a \times b||=||a||||b||sin\theta$$
有意思的是,该结果正好等于 a、b 按平行四边形法则形成的四边形的面积:
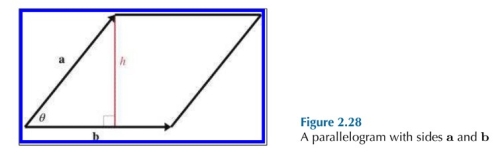 假设 b 为底,那么 高 $h=||a||sin\theta$,面积的计算结果为 $||b||\cdot||a||sin\theta$,与之前的叉乘的结果正好符合。
假设 b 为底,那么 高 $h=||a||sin\theta$,面积的计算结果为 $||b||\cdot||a||sin\theta$,与之前的叉乘的结果正好符合。
当 a、b 平行的时候,$sin\theta = sin(0) = 0$,因此两个平行向量的叉乘结果为一个零向量。几何上来说,因为零向量垂直于任意向量,因此可以解释该代数计算结果。
叉乘结果的方向
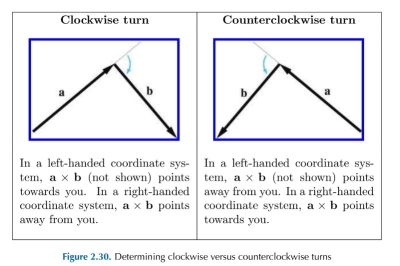
叉乘结果的方向根据坐标系的不同会有不同的计算方式。一般的方法是将参与运算的第二向量的尾部至于第一向量的头部,通过该方式来判断第一向量的旋转方向。在左手坐标系中:
- 如果是顺时针方向,叉乘结果指向我们自己
- 如果是逆时针方向,叉乘结果指向屏幕里边
右手坐标系的结果与上述的结果完全相反。
 如果指定 $\vec{x},\vec{y},\vec{z}$ 为与坐标轴方向相同的单位向量,那么无论什么坐标系都适用于以下规则:
如果指定 $\vec{x},\vec{y},\vec{z}$ 为与坐标轴方向相同的单位向量,那么无论什么坐标系都适用于以下规则: