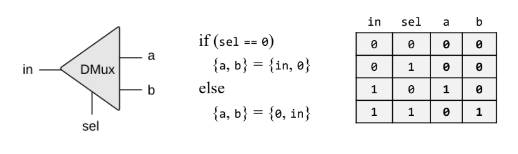目录
Week1
Week 1 notes
Introduction
- How: Implementation
- What: Abstraction
Multiple layers Abstraction
Design a chip
Folder Structures
Boolean Functions and Gate Logic
Boolean 使用 0 和 1 表示状态。
Boolean Logic
Operations & Expressions
Boolean 的基础运算有三种:AND / OR / NOT。其结果可以用真值表(Truth Table)表示:
以上的这些逻辑运算可以组合成复杂的表达式,比如:
1 AND (0 OR (NOT (1)))Boolean Functions
如果将表达式中的 0 和 1 以变量表示,那么得到的函数就被称为逻辑函数(Boolean Functions):
f(x,y,z) = (x AND (y OR (NOT (z))))(x,y,z) = (1,0,1) 时,其真值表为:
可见逻辑函数可以用函数或真值表的方式来表达。
Boolean Identites
# Commutative
(x AND y) = (y AND x)
(x OR y) = (y OR x)
# Associative
(x AND (y AND z)) = ((x AND y) AND z)
(x OR (y OR z)) = ((x OR y) Or z)
# Distributive
(x AND(y OR z)) = (x AND y) OR (x AND z)
(x OR(y AND z)) = (x OR y) AND (x OR z)
# De Morgen (when NOT involved)
NOT(x AND y) = NOT(x) OR NOT(y)
NOT(x OR y) = NOT(x) AND NOT(y)
#Idenpotence
x AND x = x
#Double Negation
NOT(NOT(x)) = xBoolean Functions Synthesis
真值表是通过逻辑函数使用不同的变量计算出来的。但在硬件设计的过程中,这个过程是相反的。我们已经知道结果(真值表),而我们希望得到实现这个结果的功能(硬件/逻辑函数)。
将真值表转换为表达式
一种方法是构建真值表的析取范式 (Disjunctive Normal Form)。其步骤:
- 按行遍历真值表,找出所有函数值为
1的行 - 对每符合条件的行,写出一个能够得到函数值的逻辑函数
- 将得到的所有符合条件的逻辑表达式,进行 OR 运算
# line 1
NOT(x) AND NOT(y) AND NOT(z)
# line 3
NOT(x) AND y AND NOT(z)
# line 5
x AND NOT(y) AND NOT(z)NP hard problem & Theorem
上述的三个表达式进行 OR 运算以后,还存在着化简的空间。化简的结果可能存在多种,也存在一个最短的表达式。我们将求这个最短表达式的问题称为NP困难问题 (NP hard problem)。
但无论如何,已经被证明的是:
Any Boolean function can be repersented using an expression contining AND, OR, NOT operations.
也就是说,无论效率怎样,所有的逻辑函数,都是可以通过有限的逻辑运算来表达的。不过,该定理可以被进一步的简化:
Any Boolean function can be repersented using an expression contining AND, NOT operations.
证明的过程很简单:如果可以用 AND 和 NOT 表示 OR,那么上面的推论就是成立的:
# proof
# using De Morgen
(x OR y) = NOT(NOT(x) AND NOT(y))NAND function
计算机学家们总结出了一种逻辑函数,NAND,用于作为构建逻辑表达式的基础。其真值表如下:
其逻辑表达式为:
$$
\texttt{(x NAND y) = NOT (x AND y)}
$$
NAND 的好处在于,只要使用这么一个逻辑运算,就能表达出所有的逻辑表达式。证明的过程也很简单:只要证明 NAND 既可以实现 AND,又可以实现 NOT 即可:
## proof
# NOT
NOT(x) = (x NAND x)
# AND
(x AND y) = NOT(x NAND y) -> ((x NAND y) NAND (x NAND y))Logic Gates
门(Gate,也称为(Chip))是一种实现了逻辑函数的物理设备。gate 的描述分为两个部分:
- 接口(Interface)来诠释其功能。其 obstruction 只能有一种
- 实现:可以有非常多种
gate 根据复杂性也分为两种:
- Elementary(Primitive) gate: 比如 AND, OR, NOT, NAND。
- Compulicated gate:通过组合基础逻辑运算的逻辑函数的实现。
gate 的接口与逻辑函数的输入和输出是一致的,不同的是其实现的方法。
Elementary logic gates: NAND
Elementary logic gates: And, Or, Not
Composite gates
Circuit implementations exmaple
AND:
- 使用了灯泡来表示 output,灯亮为
1,灯灭0 - 使用了relay 来作为输入:开着的时候为
1,关着的时候为0。显然,只有 relaya和b都开着时,灯才会亮。
- 任意一个 relay 连上时,灯都会亮:
物理层面的实现是 EE 的内容。CS 只关注功能实现。
Design with HDL
Hardware Description Languge(HDL) 是一种允许设计者在电脑上设计并模拟测试硬件结构的语言。设计者可以通过 HDL 模拟硬件,并在硬件模拟器中使用,测试。一个典型的 HDL 程序应该包括如下的信息:
- Interface
- 硬件的功能描述
- 硬件名
- 硬件的输入输出
- Implementaion
比如下面的例子:
/** API documentation: what the chip does. */
CHIP ChipName {
IN inputPin1, inputPin2, ... ;
OUT outputPin1, outputPin2, ... ;
PARTS:
// Here comes the implementation.
chipPart(connection, ... , connection);
chipPart(connection, ... , connection);
}
HDL 是一种静态描述语言(functional & declarative)。HDL 的执行会在之后交给解释器执行,但 HDL 编程本身不涉及任何的执行。因此,HDL 可以以任意顺序书写。
即便如此,为了维护可读性,HDL 的约定是按照设计图,从左到右依次描述 gate.
Design I : General Idea
Design II : Gate diagram
根据上述的信息,可以将上面的逻辑转化为包含基础逻辑运算的 idea:
out = 1 when:
a And Not(b)
or
b And Not(a)- 根据之前 idea 中的逻辑,
a和b都产生了两路信号。以a为例,存在a和Not(a)的信号。我们需要根据这些信号将存在的链接画出来:- 画出每一个链接
如果设计中使用了别的成品 gate (off the shelf gate),其命名和输入输出必须严格按照其定义在设计图上标记。
Design III: Describing diagram with HDL
接下来的工作是如何将上面的设计图用 HDL 表达出来。HDL 的描述也分为接口和实现两部分:
- 接口(header):描述目标芯片 的输入输出(XOR)
- 实现:从左到右描述所有实现中用到的芯片的输入输出,以设计图中的命名(Inner Pins):
/** out = (a And Not(b)) Or (Not(a) And b)) */
CHIP Xor {
IN a, b;
OUT out;
/* implementations */
PARTS:
Not(in = a, out = nota);
Not(in = b, out = notb);
And(a = a, b = notb, out = aAndNotb);
And(a = nota, b = b, out = notaAndb);
Or(a = aAndNotb, b = notaAndb, out = out);
}Hardware simulation
当完成 HDL 的设计后,我们使用硬件模拟器对其进行测试。测试可以通过:
- 模拟器本身(Interactive)
- Scripting Based
测试完毕后都会得到一个结果文件(compare files)用于验证测试结果。
Interactive simulation
测试的过程:
- 加载 HDL
- 赋予输入端不同的数据(0 & 1)
- 验证结果:
- out pins (
out) - internal pins
Scirpt-based simulation
我们可以通过创建后缀为 .tst 的文件来手动指定需要运行的测试。下面脚本示例可以用于测试 XOR:
// loading file
// every chips reload before each testing
load Xor.hdl;
// series of test command
set a 0, set b 0, eval;
set a 0, set b 1, eval;
set a 1, set b 0, eval;
set a 1, set b 1, eval;Result file
测试后,模拟器会返回一个后缀为 .out 的结果文件。如果我们的 HDL 正确,那么返回的结果会与真值表一致。比如 XOR 正确的返回:
| a | b | out |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |.out file 的输出可以在 .tst 文件中设置:
//setting output file
output-file Xor.out;
//output
set a 1,
set b 1,
eval,
output;compare file
对于比较复杂的检测,我们不可能去一位一位的检查结果是否正确。通用的做法是使用 .cmp 文件存储正确的真值表结果,并使用之前生成的 .out 文件与其进行对比。比较的过程是按行比较,如果两行不相同,那么模拟器会报错。
.cmp 文件的指定也是在 .tst 文件中设置:
// compare result with file
compare-to Xor.cmp;
comapare 文件是如何制作的?
就像我们生成 out 文件一样,compare 文件是通过正常的测试流程来制作的。唯一不同的是,我们使用高级语言(比如 JAVA),而不是 HDL 来制作 compare 文件。该过程被称为 Behavioral simulation。
硬件开发的流程
- 首先由系统架构师提出需求,并交由团队中的所有人来讨论实现方法
- 系统架构师来决定哪些基础芯片需要设计
- 对于每个基础芯片,系统架构师会指定
- 芯片的 API
- 测试脚本(
.tst) - 校验文件(
.cmp)
- 开发者进行开发(使用 HDL)
Multi-Bit Buses
在硬件的设计过程中,有时候需要对一组 bit 进行操作(比如数字,就可以被视作是一组 16 位 的 bit)。这一组 bit 往往被我们视作整体,并称之为 buses(拉丁语,many or multiple 的意思)。为了支持此类操作, HDL 中提供了相应的实现方法。
以两个数字相加为例,门实际上接收的是两个 16 bit 的数据,返回的是一个 16 bit 的数据:

buses in HDL
上述的 gate 在 HDL 的定义可以写为:
/* Adds two 16-bit values */
CHIP Add16 {
IN a[16], b[16];
OUT out[16];
PARTS:
//...
}在 buses 中访问 Bit
buses 中访问 bit 与数组中访问元素一致,都是使用下标访问。下标也是从 0 开始。比如 a 是一个 4bit 的 bus,访问其第一个 bit 的表达式为:
a = a[0];/* ANDs together all 4 bits of the input*/
CHIP And4Way {
IN a[4];
OUT out;
PARTS:
AND (a = a[0], b = a[1], out = t01);
AND (a = t01, b = a[2], out = t012);
AND (a = t012, b = a[3], out = out);
}HDL 中的下标是从右到左的。 a[0] 是最右边一位 bit.
buses 作为输出值
buses 本身也可以作为芯片的输出,这使得按位返回得以实现。比如下面的芯片实现了按位 AND 并按位返回的效果:
/*
Computers a bit-wise and of its two 4-bits input buses
*/
CHIP And4 {
IN a[4], b[4];
OUT out[4];
PARTS:
AND (a = a[0], b = b[0], out = out[0]);
AND (a = a[1], b = b[1], out = out[1]);
AND (a = a[2], b = b[2], out = out[2]);
AND (a = a[2], b = b[3], out = out[3]);
}sub-buses 的使用
HDL 允许定义子bus。写法如下:
//a full bus
a[16];
//two sub buses
a[0..7];
a[8..15];IN lsb[8], msb[8];
OUT a[16];
//specifies the sub range for lsb[8] and msb[8]
Add16[a[0..7] = lsb, a[8..15] = msb, b=..., out =...);
Add16(..., out[0..3]=t1, out[4..15]=t2);buses 的几个惯例
- sub-buses 输出时,允许输出的 sub-bus 在选择带宽位时有重叠。
- 内部 pin 的带宽会被自行的推断,比如下面两种情况:
// 16bits input is truncated in 14bits output
Add16(a=Bus1[0..15], b=Bus2[0..15], out[0..14]=out2[0..14]);// single bit width
x = lsb[i];
//j-i+1 bit width
y = lsb[i..j];true和false可以对所有的 bits 进行初始值设定(对应0和1)
Add16(a=true, b=false, out=out2);internal pin 不允许使用下标访问,比如 y[i] 是非法的。
Elementary Gates
Not Gate
And Gate
Or Gate
Xor Gate
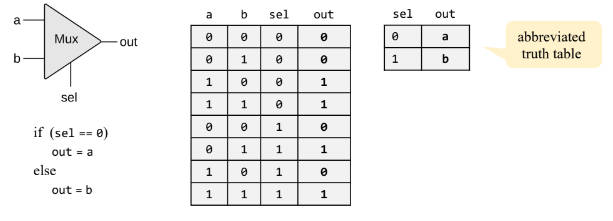
Mux Gate
- Multiplexor(Mux) 充当了一个 switch 的角色,通过
sel的开启和关闭可以选择接入a还是b。 sel可以输入周期性的信号,可以使输出在a和b之前自动切换。
- 实现:
$$\texttt{Mux(a, b, sel) = (a And Not(sel)) Or (b And sel)}$$
这类带开关的逻辑门通常可以用来创建可编程逻辑门(programmable gate)。将不同功能的门接入 MUX 即可通过 sel 信号来控制使用不同的逻辑门。
DMux Gate
- Demultiplexor(Dmux) 是 Mux 的反向操作,可以将单个输入分解为两个输出
- 实现:
\[
\begin{align*}
&\texttt{DMux(in, sel)} \\
&\texttt{a = in And Not(sel) }\\
&\texttt{b = in And sel}
\end{align*}
\]
传输过程中通常使用单路的 bit 串进行数字传输。通常传输链路都会非常长(几千公里),如果需要同时输送两组信号源比如(AAAAA… 和 BBBBB…,这种情况下比较经济的做法是将信号进行 MUX,同时将 sel 设定为周期信号(oscillator)。
经 MUX 后的信号会将两组信号源按照 bit 位单位进行交叉输出(比如输出ABABABAB…),然后在接收方通过 DMUX 以同样的 sel
进行分解来得到 A 和 B。
作业中通常涉及到组多路的基础门。这种牵涉到多路的情况一般都是用一个多 bits 的 sel 来控制输出状态。只要搞清楚哪一位 bit 控制的是哪一个层级的 switch 即可。层级可以通过真值表来判断。比如 4 way 的需要用 00 01 10 11 来控制。如果 00 对应 a, 01 对应 b,发生变化的只有 index 0,因此其控制层级就为 sel[0]。
另外一点需要注意的是区分多个输入和多个输出的情况:
- 多个输入的情况,输入的时候需要先通过低层级的选择器筛选,才能将结果交给更高层级的门进行运算
- 多个输出的情况则完全相反;首先需要从最高层级进行划分,再对 sub-group 进行次层级的选择,以此类推。