week 1 notes

• <Control>-P (previous)
• <Control>-N (next)
• <Control>-D exits a session

# import lib from specific url
from urllib.request import urlopen

编程语言通常会提供三种方式来生成复杂的指令：

• primitive expressions and statements: 编程语言提供的最基础的单位
• means of combination: 由最简单的单位组合而成的复合指令
• means of astraction：复合指令可以被抽象，也就是将复合指令命名，并整合为一个单元来使用。

• data：需要被操作的内容
• function：制定如何操作 data 的规则

表达式包括两种：

• primitive expressions：比如数字，通常以算数表达式的组合形式出现（operand + operator(infix) + operand）
• call expressions

call exressions 是复合表达式的一种，是 $f(x)$ 的一般形式，指计算（mapping）的过程。其特点：

• 组成：函数的名字，括号，参数（argument）
• 参数可以有多个，如果有输出，输出也可以有多个。
• 可嵌套

call expressions 通常是如下的形式：

name 是一种用于关联 computational objects 的方式。name 可以通过与该对象绑定（binding）的方式来与其关联，从而达到通过 name 来操作该对象的目的。name 的绑定方式有 3 种：

• import：从外部导入已绑定的 name，使其对本地可见
• assignment：最简单的抽象方法；使用自定义的 name 和赋值操作，将 name 与对象关联
• define a function：以函数的方式将自定义的 name 与对象关联，对象通常是复合对象。

由于这种绑定关系的的存在，计算机需要分配一部分空间存储这些 name, object 以及关系。被分配的空间被称为环境（environment）。下面是 python 的示例：

#binding example
#import name with bound function

>>>from math import sqrt
>>>sqrt(256)

#assign name to a value
>>> radius = 10

#assgin name to an function
>>> max
#<built-in function max>
>>>f = max

#define a function
def square(x):
    return x*x

• built-in function 的 name 可以直接与其他对象绑定
• 每次修改 name 对应的数据时，都需要进行独立赋值。只修改一个 name 并不会影响其他 name 绑定的值：

>>> area, circumference = pi * radius * radius, 2 * pi * radius
>>> area
314.1592653589793
>>> radius = 11
>>> area
314.1592653589793
#another assignment needed for updating the value of area
>>> area = pi * radius * radius
380.132711084365

• 赋值操作符右边的所有表达式都会在与 name 绑定之前先被衡量，比如下面的交换，x,y 先被取值，再进行了重新绑定：

>>> x, y = 3, 4.5
>>> y, x = x, y
>>> x
4.5
>>> y
3

基础的解释顺序为：

1. operator
2. operand（可能是 primtive expr，也可能是 subexpression）
3. subexpression 的 function (operator)

特点是：要计算主表达式，就得先计算出其子表达式的值。这种评估的过程被称为递归（recursive）

如果 operand 是子表达式(sub-expression)，那么对该表达式按基础顺序继续执行，直到得到值（value）。例子如下：


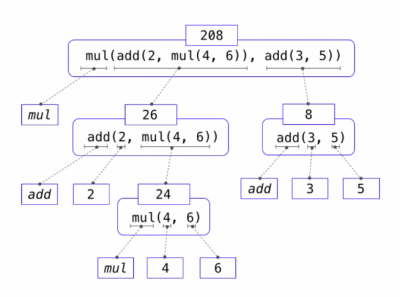
该结构被称为表达式树（expression tree）

• environment 提供 name 的意义，以及评估 name 的环境。无意义的 name 参与的运算也是意义的
• statement 不会被评估，但会被执行（exxcuted）；也就是说，statement 修改 name 的内容，但不会输出新的内容。比如：

# the operation does not return any values, but changes value of x
x = 3

纯函数（pure function）指有输入（argument）并会产生输出 (the result) 的函数，比如：

>>> abs(-2)
2

• 纯函数只影响其输出结果（返回值）
• 相同参数的纯函数返回结果也相同

非纯函数（Non-pure functions）指应用时带有“副作用（side effects）” 的函数（通常指改变解释器状态）。打印是一种常见的副作用：

>>> print(1, 2, 3)
1 2 3

>>> print(print(1), print(2))
1
2
None None

• 在复合的情况下，纯函数会更可靠
• 纯函数可以更有效的被用于函数的嵌套中
• 纯函数测试起来简单（同样的 argument 永远都会返回对应的结果）

自定义函数是抽象过程中更加高级的做法。这种做法允许我们将 name 绑定到指定的复合指令集合上。比如这段程序：

>>> def square(x):
        return mul(x, x)

def <name>(<formal parameters>):
    return <return expression>

environments 通过一系列的 frame 来衡量表达式。以 frame 为单位，每个 frame 内部都会存储对应的 name，以及该 name 绑定的 value.

在 python 中，默认存在一个全局（golbal）frame。赋值 / 外部导入的 name 都会存储在这个 frame 中：


function 的 binding (无论是导入的，还是自定义的)，也存储在这里：


我们将存储在 frame 中的 name 称为 bound name，而出现在函数内部的，同样的 name 称为 intrinsic name。每个函数可以同时存在多个 bound name，但 intrinsic name 有且只有一个。

• bound name 会在评估期间完成绑定。
• Function Signatures：通过描述参数（formal parameter）的数量来区分同名的不同函数。

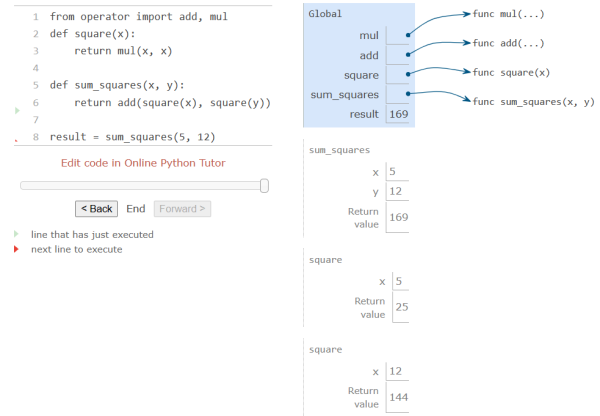
考虑以下函数：

from operator import add, mul
def square(x):
    return mul(x, x)

def sum_squares(x, y):
    return add(square(x), square(y))
	
    result = sum_squares(5, 12)

1. 首先，python 会评估 name sum_squares. 此时 sum_squares 与自定函数绑定，其关系存储在 global frame 中。
2. 当程序执行到调用 sum_square()，也就是 result = sum_squares(5, 12) 这一步时，此时：
   1. 该调用创建了一个 sum_suqare() 专属的 local frame
   2. local frame 中保存了 sum_suqare() 内部 operand 的绑定关系。此处是 square()。需要注意的是这里的 operator add() 是 built-in（外部导入的），因此其绑定存储在 global frame 中，而不是 sun_square() 的 local frame 中
3. 接下来需要应用另外一个自定义函数 square()，因此针对该函数的绑定，需要再创建一个 Local frame 进行存储
4. 执行完毕之后，将得到的结果一级一级往上反馈，最终得到最后结果：

可以发现的是：

• 存储与 global frame 中的 name 是可以共享的
• 基于 local frame 的 name，是独立的；比如上例中的 x，即便 name 相同，根据其所在的 local frame, 其绑定的 value 也不同。

函数的实现与其 formal parameter 无关。比如下面的两个函数实际上是同一个：

>>> def square(x):
        return mul(x, x)
>>> def square(y):
        return mul(y, y)

• 避免了 formal parameter 的 name 与 global frame 中的 name 同名带来的问题。
• 确保了 formal parameter 是基于函数独立的；避免了多个函数之间因为参数重名而带来的冲突

我们将 local name 生效的区域（函数体）成为它的 scope。如果某个 name 无法被访问，那么我们就称其 out of scope。

• lowercase, spearated by underscores
• 函数名通常表示操作的类型（比如 print()），或是得到的结果（比如 max）
• argument 使用 lowercase, spearated by underscores，一个词的 name 更好
• argument 的名字同样也应该表意
• 不推荐使用单字母参数

从之前的例子可以看到，我们在不考虑 square() 如何实现的情况下使用 sum_squares() 函数。我们将 square() 这种处于另一个函数内部的函数实现称之为函数抽象(functional abstraction)。从这点上来看，下面两个函数是没有区别的：

# these two functions are indistinguishable becuase of their return value
>>> def square(x):
        return mul(x, x)
>>> def square(x):
        return mul(x, x-1) + x

函数抽象需要考虑三个核心的属性：

• The domain of a function: 函数可以接受的参数范围
• The intent of function：函数的 input 与 output 之间的关系
• The range of a function: 函数返回值的取值范围

• / / 是 floor division, / 是一般除法，分别对应 floordiv() 和 truediv()

函数设计应该遵循一个 idea:

functions are abstractions.

具体的来说：

• 每个函数应该只对应一项工作，该工作可以很简单的描述。多个工作应该使用多个函数实现
• DRY(do not repeat yourself)。逻辑只需要被实现一次，并反复应用；而不是到处拷贝该逻辑
• 函数应该被定义为更泛化的形式。比如比起 square() 函数，我们应该实现的是 pow() 函数。因为指数运算包含了平方运算。

python 中通常包括了函数的描述，这类 documentation 被称为 docstring：

• docstring 使用首尾三对双引号包含
• docstring 需要遵循缩进

>>> def pressure(v, t, n):
        """Compute the pressure in pascals of an ideal gas.

        Applies the ideal gas law: http://en.wikipedia.org/wiki/Ideal_gas_law

        v -- volume of gas, in cubic meters
        t -- absolute temperature in degrees kelvin
        n -- particles of gas
        """
        k = 1.38e-23  # Boltzmann's constant
        return n * k * t / v

statement 与 expression 在本质上有不同：

• 我们评估（evaluate） expression
• 我们执行（execute）statement

statement 意味着应用更改：比如赋值，返回等等。exrepssion 在被评估的时候也可以被视作 statement，但其生成的结果会丢失。比如：

>>> def square(x):
        mul(x, x) # Watch out! This call doesn't return a value

>>> def square(x):
        return mul(x, x)

结构如下：

<header>:
    <statement>
    <statement>
    ...
<separating header>:
    <statement>
    <statement>
    ...
...

上述的结构可以被视作 sequence，也就是该结构总可以分为两个部分：

• 当前的 statement
• 余下的 statement

这是一种递归的结构。

用户自定义的函数是在对应的 local frame 中运行的。local frame 在该函数被调用时创建；函数体中的 return statement 会起到重定向的作用。函数什么时候结束取决于

• 第一个 return statement 什么时候被执行
• 返回的值

赋值语句可以处于函数内部。任何函数内部的赋值，其绑定信息都存储于local frame，对外部的 name 不造成任何影响。

if <expression>:
    <suite>
elif <expression>:
    <suite>
else:
    <suite>

• 首先会评估 header
• 某个 header 为 true, 则执行该 Header 下的 suite，其他的 suite 将会被跳过。

while <expression>:
    <suite>

python 中可以使用 assert statement 做验证。如果 assert 返回的对象为 True，那么什么也不会发生。否则，错误会被抛出：

>>> def fib_test():
        assert fib(2) == 1, 'The 2nd Fibonacci number should be 1'
        assert fib(3) == 1, 'The 3rd Fibonacci number should be 1'
        assert fib(50) == 7778742049, 'Error at the 50th Fibonacci number'

docstring 中可以包含 test case，用于测试：

>>> def sum_naturals(n):
        """Return the sum of the first n natural numbers.

        >>> sum_naturals(10)
        55
        >>> sum_naturals(100)
        5050
        """
        total, k = 0, 1
        while k <= n:
            total, k = total + k, k + 1
        return total
        
>>> from doctest import testmod
>>> testmod()
TestResults(failed=0, attempted=2)