Differentiation / 微分

MITx: 18.01.1x Calculus 1A notes

Linear Approximation

来看一个例子：

假设我们有一条船在运河里航行。我们用 $y$ 表达船在河里航行的距离（m），用 $t$ 来表达船在河中航行的时间（s），那么船在河中航行的距离与时间的关系就可以写成：
$$y=f(t)$$

如果我们知道船在 20 秒的时候船只航行了 150 米，且此时船只的速度为 0.4 $m/s$。那当船只在 30 秒的时候，我们是否能算出此时船只航行的距离呢？

很显然的是，我们没有足够的数据算出 $f(t)$ 的表达式。因此，如果需要算出 $f(30)$，我们就需要假设在 20 到 30 秒这个时间段内，船只是以 20 秒处的速度在匀速向前进的。根据以上的假设，不难得出：

$$f(30) \approx f(20) + 0.4 * \Delta t = 150 + 4 = 154$$

线性近似的公式推导

上面的例子可以抽象为以下的图像：

也就是说，我们已知了函数的斜率（速度），以及其过的点（$x(20) = 150$）,如果假设斜率（速度）不变的话，我们就可以估算未来某个时间能达到的距离（比如 $x(30)$）。这个距离的变化两近似于变化的时间 $t$ 与速度的乘积；加上之前已经走过的距离即可得到估算的结果。

什么是 linear Approximation?

上例中，我们实际上是在用函数上某一点的切线方程，代替函数进行计算。这是因为过某一点的切线与该点附近的函数图像非常接近。由于切线是线性函数，我们将以切线代替函数作为计算标准的方法称为线性近似（Linear Approximation）。

计算的过程：

求导数（斜率）
使用斜率乘以 $x$ 的变化量，得到 $y$ 的变化量
将 $y$ 的变化量与原有 $y$ 的量相加

线性近似一般公式的推导

为什么可以使用切线近似函数？

假设函数为 $g(x)$，已知：

函数在 $x_{0}$ 点的值
函数在$x_{0}$ 处的斜率($g'(x_0)$)

现在我们希望求函数上另外一个点 $x$ 的值：

首先，我们需要近似出 $g$ 的变化量 $\Delta g$，该变化量等于斜率与 $x$ 的变化两 $\Delta x$ 的乘积

推广一下，有以下过程：

\begin{align} \Delta g &= m* \Delta x \\ &\Rightarrow g(x) - g(x_0) \approx g'(x_0)*(x-x_0) \\ &\Rightarrow g(x) \approx g'(x_0) \cdot (x-x_0)+g(x_0) \end{align}

可以看出，左边是我们的函数图像，右边是 $g(x)$ 在$x_0$处的 切线公式。也就是说，切线近似于函数。

为什么可以用斜率与 $x$ 的乘积表示变化量？

根据斜率 $m$ 的定义 $\displaystyle \lim_{\Delta x \to 0}\frac{\Delta g}{\Delta x}$，可以得出结论：当 $\Delta x$ 特别小，也就是 $x$ 与 $x_0$ 两点非常接近的时候，我们就可以使用切线代替函数进行近似计算。

线性近似的正式定义

$$ \displaystyle f(x) \approx \left. \frac{df}{dx} \right|_{x=a} \cdot \Delta x \qquad \ \mathrm{for} \ \Delta x \ \mathrm{near} \ 0 $$
$$ f(x) \approx f'(a) (x-a) + f(a) \ \ \ \mathrm{for} \ x \ \mathrm{near} \ a $$

二阶导数与近似结果

在线性近似中，由于函数在对应点的导数（斜率）已知，对应的二阶导数也可以求出来。该二阶导数可以用于判断两件事情：

近似的结果是高估还是低估
近似结果的误差的增大趋势是快还是慢

第一点可以通过二阶导数的正负得知：

如果二阶导数为负，则在对应点的函数图像是 concave down 的。这就意味着，函数的图像实际上在切线以下；因此线性近似的结果大于实际的函数结果
反之，如果二阶导数为正，则线性近似的结果小于对应的函数结果

第二点可以通过二阶导数的绝对值大小得知。二阶导数反映了当前导数变化的速率；绝对值越大的二阶导数会导致导数的变化率越大，那么函数偏离切线的趋势就会越快；反之越慢。

Product Rule

某些情况下我们的函数可能牵涉到好几个变化的情况。这种情况下，我们很可能需要对好几个单变量函数的变化量进行相乘（也就是导数相乘）。这时候我们需要使用 Product Rule 来处理这样的问题。

一个典型的例子就是求长方形面积的变化量。假设有一个长方形，它自身的长宽（单位 $m$）都在根据时间（单位 $t$）的变化而变化。我们假设其长边的长度与时间的关系为 $f(t)$，宽边的长度与时间的关系为 $g(t)$。那么长方形面积的变化就是基于两个边的变化量的乘积。

Product Rule 的推导

为什么面积增长量不等于 f'(t)g'(t)

但注意的是，尽管导数的乘积在形式上表现为$ f'(t) \cdot g'(t)$，但实际上我们并不能直接这么做。原因很简单：单位不匹配。按照上面的例子：

长 / 宽长度的增长量（导数）的单位是 $m/s$。
长方形面积增长的单位应该是 $m^2/s$。

如果我们直接做 $f'(t) \cdot g'(t)$ 的乘法，那么那么得到的单位则是 $m^2/s^2$。即便是数学结果相同，但实际上这两者测量的并不是同一样事物。

正确的解决方案

对此，我们的解决方式是将长宽的变化对长方形面积带来的变化进行分别计算，然后再将得到的结果相加，这样得到的单位就和长方形面积增长的单位匹配了，即：

$$h'(t) = f(t) \cdot g'(t) + g(t) \cdot f'(t)$$

<html>

</html>

Product Rule 的证明

从相对正式的推理过程来说，当 $h(t) = f(t)\cdot g(t)$时，如果想得知 $h(t)$ 的变化量，则有：$\Delta h = h(t_{new}) - h(t)$。而显而易见的是：

\begin{align} h(t) &= f(t) \cdot g(t)\\\\ h(t_{new}) &= f(t_{new}) \cdot g(t_{new})\\\\ &=(f(t) +\Delta f) \cdot (g(t)+\Delta g) \end{align} 因此，对于 $h(t)$ 的增长量 $\Delta h$，则有：

\begin{align} \smash\Delta h &= h(t_{new}) - h(t) \\\\ & =f(t_{new}) \cdot g(t_{new}) - f(t) \cdot g(t)\\\\ & =(f(t) +\Delta f) \cdot (g(t) +\Delta g) - f(t) \cdot g(t) \\\\ & =f(t)\cdot\Delta g + g(t)\cdot\Delta f + \Delta f \cdot \Delta g\\\\ \end{align}

因此，对于 $h'(t)$，根据 Linear Approximation 的定义，则有：

\begin{equation}\begin{split} h'(t) &\approx \lim _{\Delta t\rightarrow 0} \frac{\Delta h}{\Delta t}\\\\ &= \lim _{\Delta t\rightarrow 0} \frac{f(t)\cdot\Delta g + g(t)\cdot\Delta f + \Delta f \cdot \Delta g}{\Delta t}\\\\ &=\lim _{\Delta t\rightarrow 0} \frac{\Delta g }{ \Delta t} \cdot f(t) + \lim _{\Delta t\rightarrow 0} \frac{\Delta f}{ \Delta t} \cdot g(t) + \lim _{\Delta t\rightarrow 0} \frac{\Delta f}{ \Delta t} \cdot \frac{\Delta g}{ \Delta t} \cdot \Delta t\\\\ &=f(t) \cdot g'(t) + g(t) \cdot f'(t) \end{split}\end{equation}

Product Rule 的正式定义

If $h(x)=f(x)g(x)$, then
$$h'(x)=f(x)g'(x)+g(x)f'(x)$$
at all points where the derivatives $f'(x)$ and $g'(x)$ are defined.

单个点存在乘积关系并不能代表可以使用 product rule. 使用 product rule 的前提是对于定义域的所有 $x$ 都有 $h(x) = f(x)g(x)$

Product Rule 的小推广

product rule 可以推广到多个函数的乘积，将其中一个函数与和其他所有函数视作两个函数即可。简单的三函数推导：

\begin{align} (uvw)' &= u'(vw) + (vw)'u \newline &=u'vw + (v'w + w'v)u \newline &=u'vw + v'uw +w'uv \end{align}

Quotient rule

我们在微分的过程中，通常还会遇到求形式为两个函数商的导数。与求两个函数乘积的导数类似，我们并不能直接将其的导数相除，因为这样会导致单位的错误。对于函数的商的导数，我们可以利用 Product Rule 和 linear Approximation 进行辅助推导。

Quotient rule 的推导

对于任意函数 $h(t) = \frac{f(t)}{g(t)}$，有

$$ h('t) = \lim _{\Delta t \rightarrow 0}\frac{\Delta h}{\Delta t} $$

对 $\Delta h$ 进行展开，则有：

\begin{align} \Delta h &= \frac{f(t)+\Delta f }{g(t) + \Delta g} - \frac{f(t)}{g(t)}\\\\ &=\frac{f(t)\cdot g(t)+\Delta f\cdot g(t) - f(t)\cdot g(t)-f(t)\cdot \Delta g}{g(t)^2+g(t)\cdot \Delta g}\\\\ &=\frac{\Delta f\cdot g(t) - f(t)\cdot \Delta g}{g(t)^2+g(t)\cdot \Delta g} \end{align}
因此，函数的商的导数可以有如下推导：

\begin{align} \displaystyle \lim _{\Delta t \rightarrow 0}\frac{\Delta h}{\Delta t} &= \lim _{\Delta t \rightarrow 0}\frac{\frac{\Delta f\cdot g(t) - f(t)\cdot \Delta g}{\Delta t}}{g(t)^2+g(t)\cdot \Delta g}\\ &=\lim _{\Delta t \rightarrow 0}\frac{f'(t) \cdot g(t) - f(t) \cdot g'(t)}{g(t)^2+g(t)\cdot \Delta g} \end{align}

因为 $\Delta g = g(t + \Delta t) - g(t)$，因此在 $\Delta t \rightarrow 0$ 的时候， $\Delta g$ 也是趋近于 $0$ 的。因此，我们就可以得到如下结论：

$$ h('t) = \lim _{\Delta t \rightarrow 0}\frac{f'(t) \cdot g(t) - f(t) \cdot g'(t)}{g(t)^2+g(t)\cdot \Delta g} = \frac{f'(t) \cdot g(t) - f(t) \cdot g'(t)}{g(t)^2} $$

Quotient rule 的正式定义

if $h(x) = \frac{f(x)}{g(x)}$ for all $x$, them ：
$$ h'(x) = \frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}$$
at all points where $f$ and $g$ are differentiable and $g(x) \ne 0$。

通俗的记忆方式：“ high-D-low minus low-D-high, all over low-low”

将 $x^{-n}$ 写作 $1/x^n$ 的形式，可以通过 quotient rule 证明 power rule 的负指数形式。
所有除 $sin(x)$ / $cos(x)$ 的常见三角函数都可以使用 quotient rule 求出其导数。

Chain rule

在现实生活中，关系往往是复合形式的。比如温度高低与距离的远近有关系，而距离又跟时间有关系。那么设想一下，如何建立起时间与温度的关系？
上述的函数关系很容易写成复合的形式：比如 $h(x) = f(g(x))$。如果我们需要通过 $f(x)$ 与 $g(x)$ 来求 $h(x)$ 的变化率，那么我们也应该知道如何计算复合函数的导数。这正是 Chain Rule 要解决的问题。

需要注意的是，变量在发生变化后，对应的单位也发生变化了。比如课程中的例子 $x = g(t) = f(u)$，但 $g'(t) != f'(u)$，因为 $g'(t) = \frac{dx}{dt}$，单位是 $m/min$，而 $f'(u)=\frac{dx}{du}$，单位是 $m/s$。本课的重点之一也是找出这两者之间的转换因子（conversion factor），比如这里： $$ \frac{dx}{dt} = \frac{dx}{du} \cdot \frac{du}{dt} $$ 具体来说是 $120m/min = 2 m/s \cdot 60 s/min$，也就是说，只要知晓当 u 发生变化时， t 变化的程度即可。

Chain Rule 的推导

以本节开头例子为例，我们可以用一张图来描述三个函数之间的关系：

<html>

</html>

根据 $T=g(d)$ 与 $d=f(t)$ ，有 $T=f(g(t))$。设 $T=f(g(t))$ 的导数为 $\frac{df}{dt}$，根据导数定义：

$$\frac{dT}{dt}=\lim_{t\to0}\frac{\Delta T}{\Delta t}$$

现在我们希望求出 $\frac {\Delta T} {\Delta t} $ 的结果。通过观察，发现 $\Delta T$ 的变化导致了 $\Delta d$ 的变化，而$\Delta d$ 的变化又引起了 $\Delta x$ 变化。如果将 $\Delta d$ 作为中间数，则有：

\begin {align} \frac{dT}{dt} &=\lim _{\Delta t\to 0} \frac{\Delta T}{\Delta t}\\
&=\lim_{\Delta t\to 0}(\frac{\Delta d}{\Delta t}\cdot\frac{\Delta T}{\Delta d})\\
& =\lim_{\Delta t\to 0}\frac{\Delta d}{\Delta t}\cdot\lim_{\Delta t \to 0}\frac{\Delta T}{\Delta d}\\
\end {align}
因为当$\Delta t \to 0$ 的时候，$\Delta d = f(t+\Delta t) - f(t)$ 也趋近于 $0$，因此上述的式子可以改写为：

\begin {align} \lim_{\Delta t\to 0}\frac{\Delta d}{\Delta t}\cdot\lim_{t\to 0}\frac{\Delta T}{\Delta d} &=\lim_{\Delta t\to0}\frac{\Delta d}{\Delta t}\cdot\lim_{\Delta d\to0}\frac{\Delta T}{\Delta d}
&=\frac{dd}{dt}\cdot\frac{dT}{dd} \end {align}
这里看起来像是 $dd$ 被“消除”了，实际上在正式的写法里并不会出现这样的误解。

正式的 chain rule 定义

if $y = f(u)$, and $u=g(x)$, then $$\left. \frac{dy}{dx} \right|_{x = a} = \left. \frac{dy}{du} \right|_{u=g(a)} \cdot \left. \frac{du}{dx} \right|_{x=a}$$

In newton notation:

if $h(x) = f(g(x))$, then
$$h'(x) = f'\left(g(x)\right) g'(x)$$
at all points where the derivatives $f'(g(x))$ and $g'(x)$ are defined.

求当 $h(x) = f(u)$，且 $u = g(x)$时,$h'(x)$ 的常见的解题顺序：

找出 $u$ 与 $x$ 之间的关系
套用 chain rule 求出带中间形式的导数结果 $\frac{df}{du} \cdot \frac{du}{dx}$
使用 $u$ 带入 $\frac{df}{du}$ 中，即可得出最后结果

比较复杂的符合情况：通过组合 product rule 和 quotient rule 将目标函数分割为子函数，再分别求出需要的 term。比较典型的类型：

$f(x)=g(x) \cdot h(x)$： product rule first
$f(x) = \sqrt{f(x)\cdot g(x)} $：chain rule first, then product rule

最终的考虑点应该基于最后一步计算该函数需要采取哪些步骤，将其作为分割函数的第一步（最后意味着最上层的步骤，第二个例子的最后一步是需要开方）。

chain rule 要求中间变量与其他变量的对应关系是一对一的。比如令直角三角形的三边为$x,y,z$（$z$为斜边）。如果 $x,y$ 同时随着时间 $t$ 在进行变化，那么我们是不能得到 $\frac{dz}{dt} =\frac{dz}{dy} \cdot \frac{dy}{dt}$ 和 $\frac{dz}{dt} =\frac{dz}{dx} \cdot \frac{dx}{dt}$ 的。这种情况下，$z$ 的函数中有两个变量 $z^2 = y^2+x^2$，因此 chain rule 不适用。
详细例子见 Unit.4 - related rates - 8. Fire truck problem

Implicit differentiation

有时候我们会遇到一些隐式方程（隐函数）。相对于显函数，这些方程并没有直接地反映明显的 $x$ 与 $y$ 之间的关系，有时候会导致求导的困难。而在几何中，隐函数往往表现为曲线（曲面）；因此对这些函数的求导的几何意义也是很重要的。因此，我们有必要研究一种新方法来对隐函数求导。

隐函数的特征

判断隐函数实际上非常简单，就看函数是否写成了 $f(x,y)$ 的形式，也就是 $y$ 是否算成了该函数里的一个变量，比如：$y^2 + x^2 = 1$ 就是一个非常典型的隐函数。隐函数也可以转换会显函数，但通常这个转换过程都非常复杂。

隐函数的求导

隐函数的求导（微分）方式通常是对方程等号两边的表达式同时求导。对于隐函数来说，等号的某一边往往是常数，因此可以利用该性质在不将隐函数转化为显函数的情况下，推算出导数的表达式。以 $y^2 + x^2 = 25$ 为例子的解法如下：

\begin {align} &y^2 + x^2 = 25 \newline &\Longrightarrow \frac {d}{dx} (y(x)^2+x^2) = 0 \newline &\Longrightarrow \frac {d}{dx} (y(x))^2 +2x = 0 \newline &\Longrightarrow 2y \cdot \frac {dy}{dx} + 2x = 0 \newline &\Longrightarrow \frac {dy}{dx} = -\frac {2x}{2y} = -\frac {x}{y} \end {align}

需要注意的是，对于因变量 $y$ 的求导，需要应用 Chain rule，因为 $y$ 是相对于 $x$ 的函数，因此对 $y$ 的求导必须同时计算内部包含的函数的导数。比如这里的 $y^2$ 求导，实际上求的是复合函数 $(y(x))^2$ 的导数，因此结果是 $2 \cdot y(x) \cdot \frac{dy}{dx}$。

上述隐函数的结果中同时有 $x,y$。这样写是没有问题的，代表着函数上任意一点的斜率都可以用 $-x/y$ 的方式来表示

隐函数求导的关键是找出 $\frac {dy}{dx}$ 的项。这些项通常由 $y(x)$ 通过 chain rule differentiate 后得到

Power rule 的分数形式证明

隐函数的导数计算方式可以用于证明 power rule 的分数形式。假设指数为分数 $m/n$，我们希望证明 $\displaystyle \frac{d}{dx}x^{\frac{m}{n} } = \frac{m}{n} \cdot x^{\frac{m}{n}-1}$。证明如下：令 $y = x^{\frac{m}{n}}$, 对两边同时 $n$ 次方，可得： $$y(x)^n = x^m$$ 此时我们得到了一个隐函数，因此对两边同时求导： \begin{align} &\frac{d}{dx}y(x)^n = m \cdot x^{m-1} \newline &\Longrightarrow n \cdot y(x)^{n-1} \cdot\ \frac{dy}{dx} = m \cdot x^{m-1} \newline &\Longrightarrow \frac{dy}{dx}= \frac{m}{n} \cdot \frac{x^{m-1}}{y(x)^{n-1}} \end{align} 此时将 $y = x^{\frac{m}{n}}$ 带入右边： \begin{align} &\frac{dy}{dx}= \frac{m}{n} \cdot \frac{x^{m-1}}{y(x)^{n-1}} \newline &\Longrightarrow \frac{dy}{dx}= \frac{m}{n} \cdot \frac{x^{m-1}}{(x^{\frac{m}{n}})^{n-1}} \newline &\Longrightarrow \frac{dy}{dx}= \frac{m}{n} \cdot \frac{x^{m-1}}{x^{\frac{m}{n} \cdot (n-1)}} \newline &\Longrightarrow \frac{dy}{dx}= \frac{m}{n} \cdot x^{m-1-(m-m/n)} \newline &\Longrightarrow \frac{dy}{dx}= \frac{m}{n} \cdot x^{\frac{m}{n}-1} \end{align}
自此得证。

某些情况下，求出来的导数可能只包含 $y$。此时需要将 $y = f(x)$ 带入进去，替换成 $x$ 为变量的表达式，才是 $\frac{dy}{dx}$ 的最终结果
函数两边不能随便化简，比如 $w^2v^3=w^3v^2$，化简以后将导致函数表示的空间维度坍塌。

Inverse Functions

有时候在两个具有关系的变量之间，我们往往希望通过彼此来确定对方的状态。而函数与反函数（Inverse Functions）则被应用到这两者之间的关系中，充当一正一反的桥梁。因此，对于反函数的学习以及的求导也是非常重要的内容之一。

反函数的定义

反函数的定义非常简单。通俗的说来，就是一个函数的作用与另外一个函数的作用完全相反，就可以称该函数为对应函数的反函数。反函数的定义如下：

If functions $f$ and $g$ satisfy $g(f(x)) = x$ and $f(g(y)) = y$, then we say $g$ is the inverse of $f$, and denote it by $f^-1$.
if a function $f$ has an inverse function $f^-1$, then $f^-1(b) = a$ if and only $f(a) =b $.

几何上来说，如果两个函数互为反函数，这两个函数上的点会关于 $y = x$ 对称（比如$(2,5)$ 与 $(5,2)$）

不是所有函数都有反函数

定义的第二段非常关键。从该段我们能看出，一个函数入股具有反函数，是从其本身是否具有 one-to-one 特性来判断的，也就是说，如果一个函数具有反函数，那么：

代数上：当 $a \ne b$ 的时候，总有 $\ f(a) \ne f(b)$
几何上：该函数的图像与任意水平线没有一个以上的交点（水平线测试）。比如抛物线（$y=x^2$），就有很多水平线与其相交；因此 $y$ 没有反函数。

总结一下正式定义：

A function f is one-to-one if $f(a)≠f(b)$ whenever $a≠b$. It is one-to-one if and only if its graph satisfies the horizontal line test (no horizontal line intersects its graph at more than one place).

某些情况下可以利用导数来判断函数是否具有反函数。比如 $g(x)=2x^3+3^x-1$，其导数为 $6x^2+3$，可以看出的是该导数恒为正，因此该函数的图像是单调递增的。也就是说，不可能与任意水平线出现两个及以上的焦点。

反函数 & 三角函数 & 导数

Partial inverses

某些函数在总的定义域上是没有反函数的。但当定义域被指定范围后，我们可以找出其在指定定义域的反函数。我们称这样的反函数为 Partial inverses。

三角函数与反函数

三角函数的反函数，也就是反三角函数 arc，正是 Partial inverses 中的典型例子。由于三角函数具有周期性，因此讨论反三角函数需要在其定义域内讨论。常见的反三角函数的定义域如下：
\begin {split} {\arcsin x} =\theta\qquad &in \qquad \left[-\pi /2,\pi /2\right] \newline \displaystyle {\arccos x} =\theta\qquad &in \qquad \left[0,\pi \right] \newline \displaystyle {\arctan x} =\theta \qquad &in\qquad (-\pi /2,\pi /2) \newline \end {split}

在计算中利用反三角函数

反三角函数作为三角函数的反函数，其因变量是和三角函数的自变量对应的，也就是 $\theta$。由于这个特性，让我们在三角函数与反三角函数的符合计算中，不用计算出 $\theta$ 的值，就可以直接求出三角函数的值。来看看例子：$tan(arccos(8/9))$：

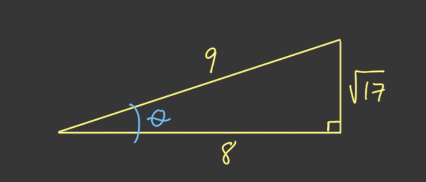
通过画图就能发现，$arccos(8/9)$ 代表的是临边 9 与斜边 8 之间的夹角 $\theta$
由 8/9 我们可以根据勾股定理算出第三边（对边）等于 $\sqrt{17}$
而求 $\theta$ 只需要用该对边除以临边即可，也就是$\frac {\sqrt{17}} {8}$

这个技巧可以用于后面的反三角函数求导。

反函数的导数

反函数的导数推导过程非常容易。由反函数与原函数的性质可以知道：

$$f(g(x)) = x$$

对等式两边同时求导，可得： $$\frac{d}{dx}f(g(x)) = \frac{d}{dx}x = 1$$

化简以后则可得到反函数的导数公式：

$$\displaystyle {g'(x) = \frac{1}{f'\left(g(x)\right)}} $$
if $g$ is a inverse (full or partial) of a function $f$, at all $x$ when $f'(g(x))$ exists and is non-zero.

从几何的描述上来看，反函数的导数则是在求目标曲线相对于 $y=x$ 的对称曲线，在目标点的斜率，如下图：

<html>

</html>

由上述图像同样也可以推导出反函数的导数公式：

$$ f^{-1}(x)' = \frac{1}{f'(y)} $$

反三角函数的求导

反三角函数的求导会利用到反函数求导的公式，以及反三角函数自身的意义。总的来说：

列出函数与反函数（三角函数与反三角函数）
将上述两个函数带入到反函数求导公式中
此时会得出$\frac{1}{f'(g(x))}$ 结构的结果，我们把注意力放到分母上
由于 $f$ 代表三角函数，其导数也应为三角函数
因此 $f'(g(x))$ 实际上是一个 $trig(arctrig)$ 的形式
此时利用反三角函数的意义即可求出分母，进而求出最后答案

反三角函数在求导中的应用

反三角函数的求导主要利用三角函数边的关系进行运算，从而避免了直接求夹角的角度。如下图的例子，对于 $sin(arccos(x))$ 的求导，可以先利用三角形边的关系算出对应的 $sin(\theta)$ 的值，再对整个函数进行导数计算。

<html>

</html>

如上图所示，这里的求导过程实际上可以写为：

$$ \frac{d}{dx}sin(arccos(x)) = \frac{d}{dx}sin(\theta) = \frac{d}{dx}\sqrt{1-x^2} =-\frac{x}{\sqrt{1-x^2}} $$

这个三角形是根据当前的三角函数构造出来的（注意：并不是一成不变的）。以 $sin(arccos(x))$ 为例，因为 $cos$ 是临边除以斜边，因此可以令临边为 $x$，斜边为 $1$，那么对应的角度正好是 $cos(x)$ 中的 $x$。此时等于我们知道了 $cos(x)$，再去算 $sin(x)$。

可见该三角形是基于 $cos(x)$ 构造出来的。如果 $\theta$ 以另外的形式（比如 $arctan(x)$），那么该三角形的构造则要以 $tan$ 的定义为准，即，领边为 $x$，对边为 $1$ 进行构造。因此，构造该三角形的策略实际上要根据 $\theta$ 的表现形式来决定的。

Exponential Functions

指数函数在非常多的领域里都有重要应用，比如生物学中的细胞分裂，物理学中的弹簧。对指数函数变化程度的评估，也是非常重要的。因此，了解如何对指数函数求导，也是非常必要的。

指数函数的求导过程推导

因为之前学习过的求导方法均不适用于指数函数，我们可以利用导数的定义公式来尝试对指数函数进行求导。因此，将指数函数带入求导公式，可有：

$$\frac {d}{dx}a^x= \lim_{\Delta x\to0} \frac{(a^{x+\Delta x}) - a^x}{\Delta x}=\lim_{\Delta x\to0}a^x\frac{a^{\Delta x}-1}{\Delta x}$$

对于上述的极限来说，$\Delta x$ 才是变化的主要原因，而 $x$ 并没变化，因此我们可以将 $a^x$ 考虑为常量，从而可以将其从极限里去掉（因为其并不影响极限的结果）。因此，我们可以得到：

$$ \lim_{\Delta x\to0}a^x\frac{a^{x+\Delta x}-1}{\Delta x} = \displaystyle a^x\lim_{\Delta x\to0}\frac{a^{\Delta x}-1}{\Delta x} $$
也就是：
$$ \frac {d}{dx}a^x = a^x\lim_{\Delta x\to0}\frac{a^{\Delta x}-1}{\Delta x} $$
令 $M(a) = \displaystyle \lim_{\Delta x\to0}\frac{a^{\Delta x}-1}{\Delta x}$ ，将其带入之前的等式中，可得：

$$\frac {d}{dx}a^x = M(a)a^x$$
可以看出，$a^x$ 的导数可以表示为一个数乘以他自身。很容易发现的是：当 $x$ 为 $0$ 的时候：

$$M(a) =\left. \frac{d}{dx}a^ x\right|_{x=0} = \lim _{\Delta x\rightarrow 0} \frac{a^{\Delta x}-1}{\Delta x}$$
可以明显的看出，$a^x$ 在 $x=0$ 处的导数等于 $M(a)$，也就是说 $M(a)$ 是 $a^x$ 在 $x=0$ 时的斜率。比如 $2^x$ 在 $0$ 处的斜率等于 $M(2)$。

指数导数的公式

$$\frac{d}{dx}a^x = M(a) a^x, $$
where the mystery number $M(a)$ is the slope of the tangent line at zero:
$$M(a) =\left. \frac{d}{dx}a^ x\right|_{x=0} = \lim _{\Delta x\rightarrow 0} \frac{a^{\Delta x}-1}{\Delta x}$$

e 的概念以及存在性证明

从上面的内容中我们知道可以用 $M(a)$ 来表示任意的底 $a$ 的指数函数在 $x=0$ 时的斜率了，但我们还是无法求 $M(a)$ 的具体值是什么。为了解决这个问题，前人们引入了一个特别的值 $e$，使得 $M(e)=1$。

我们先抛开为什么需要 $e$ 的疑问，来看看 $e$ 能达到什么样的效果。显然，当 $M(e)=1$ 的时候，我们有：

$$\frac{de^x}{dx} =M(e)\cdot e^x = e^x$$
这个性质会在之后使用对数推导指数求导公式的时候起到非常关键的作用。

e 的定义

The base $e$ is the unique real number so that: $M(e) = \displaystyle \left.\frac{d}{dx} e^x\right|_{x=0} = 1$. Then:
$$\displaystyle \frac{d}{dx}e^x = e^x.$$

e 的存在性证明

而为了证明 $e$ 是否存在，我们来考虑一下如下的推导过程：

首先我们引入一个具体的指数函数 $f(x)=2^x$来说明这个问题。很显然对于这个指数函数，我们有 $$f'(0) = m(2)$$ 假设我们为该函数添加一个系数 $k$，从几何上说也就是拉伸该函数。按照指数函数，我们有： $$f(kx) = 2^{kx} = (2^k)^x$$ 因为 $k$ 是常数，所以 $2^k$ 也应该是常数。那么理论上来说，不管是什么样的底数，都可以用 $2^k$ 来表示。

而在指数的图像中，$k$ 意味着对图像的拉伸或者挤压。这就意味着根据 $k$ 的不同，图像在 $x=0$ 的斜率是可以变化的。因此我们对 $y = {(2^k)}^x$ 求导，则可以得到函数在该点斜率的表达式：

$$ \frac{d}{dx}{(2^k)}^x = \frac{d}{dx} f(kx)= kf'(kx) $$

那么该函数图像在 $x=0$ 的时候的斜率表达式可以写成：

$$ \left. \frac{d}{dx}{(2^k)}^x \right |_{x=0} = kf'(0) = kM(2) $$

令 $b = 2^k$，有： $$\left. \frac{d}{dx}b^x \right |_{x=0} = k \cdot M(2)$$ 当 $k=\frac{1}{M(2)}$ 的时候，右边等于 1；由于 $M(e) = 1$，因此 $b = e$。至此可知 $e$ 存在。

Logarithms

上一节我们并没有解决指数函数的求导问题，而是挖了很多坑。原因是如果想解决指数函数的求导问题，我们必须知道对数的一些知识。而扮演主要角色的，则是自然对数这一概念。

简单的联系：以 $a$ 为底，值为 $x$ 对数函数是以 $a$为底，指数为 $x$ 的指数函数的反函数： $$log_a(x) ⇔ a^x$$

自然对数的导数

自然对数（Natural logarithm）是相对于指数函数 $y = e^x$ 来说的，以 $e$ 为底的对数，记做 $y = lnx$。而自然对数的求导方法可以用指数与对数的关系得出：

因为自然对数函数是对应同底的指数函数的反函数，所以我们有

$$ e^{ln(x)} = x $$

令 $ln(x) = u$，则可以得到一个隐函数：

$$ e^u=x $$

对两边同时求导，则有：

$$ \frac{d}{dx}e^u=\frac{d}{dx}x=1 $$

根据 chain rule，上面的式子可以改写为：

$$\frac{d}{du}e^u \cdot \frac{du}{dx} = 1$$

根据 7.2 中我们得到的 $e^x$ 的导数的性质，上述式子可以改写为：

$$ e^u \cdot \frac{du}{dx} = 1 $$
将 $e^u = x$ 带入上面的式子，则有：
$$ x \cdot \frac{du}{dx} = x \cdot \frac{dln(x)}{dx} = 1 $$
因此，可以得出自然对数导数的计算公式：

$$ \frac{d}{dx}ln(x) = \frac{1}{x} $$

这个公式非常的重要，因为它在求解指数函数的导数的过程中扮演了非常重要的角色。

指数函数的导数

对指数函数的求导我们有两种方式来进行计算；但无论哪种方式，我们都需要使用与 $e$ 相关的知识来进行推导。

Method 1: Changing to base e

该方法使用 $e$ 作为底数来进行指数函数的求导。如果我们希望求 $a^x$ 的导数，那么我们可以将该函数的底换成 $e$：
$$a^x = (e)^{ln({a^x)}} = e^{xlna}$$

接下来我们对两边同时求导：
\begin{split} \frac{d}{dx}a^x &= \frac{d}{dx}e^{xlna} \newline &= ln(a) \cdot e^{xlna} \newline \end{split}
将 $a^x = e^{xlna}$ 带入上面的式子，可得： $$\frac{d}{dx}a^x =ln(a) \cdot a^x$$ 根据 7.1 中推导出来的公式，我们发现之前不知道的 $M(a)$，实际上就是这里的 $ln(a)$。因此，我们就得到了指数函数的求导公式：

$$\frac{d}{dx}a^x = ln(a) \cdot a^x$$

辅助记忆：底的指数乘以底的自然对数，底是常量

Method 2: Logarithmic differentiation

有时候如果在微分函数的时候遇到困难，我们可以选择对其的对数进行求导。假设我们有函数 $u$，则对其的对数求导的过程可以写为：

$$ \begin{split} \frac{d}{dx}ln(u) &= \frac{dln(u)}{du} \cdot \frac{du}{dx}\\\\ &= \frac{1}{u} \cdot \frac{du}{dx} \end{split} $$

本方法实际上利用了对函数的对数求导可以得到函数的导数与其倒数乘积的性质。

假设 $u = a^x$，那么 $ln(u)$ 实际上可以转写为：
$$ ln(u) = ln(a^x) = xln(a) $$
对两边同时求导，可得： $$ ln(u)' = ln(a) $$

根据之前的计算， $(lnu)'$ 可以写成 $\frac {u'}{u}$，因此我们可以推导出 $u' = u\cdot ln(a)$。根据这个结果，我们也能同样得到指数函数 $a^x$ 的求导公式：

$$\frac{d}{dx}a^x = ln(a) \cdot a^x$$

利用对数形式求一般函数的导数步骤：

首先将 $f(x)$ 替换为 $u$
根据之前的推理，有 $\frac{d}{dx}ln(u) = u'/u$
接下来将函数两边同时求对数，并进行简化
最后可以得到 $\frac{u'}{u}$ 等于简化后的式子，将 $u = f(x)$ 带入计算即可。

Eule's Number: e

通过定义欧拉数 $e$ 我们可以对指数函数进行有效的求导，但我们还需要一个计算 $e$ 的具体公式。用于计算 $e$ 的方法有很多，课程中提供了一种计算 $e$ 的方式：

$$ e = \lim_{n \to \infty} \left(1+\frac{1}{n} \right)^n $$

推导过程如下：

\begin{split} \lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n\ &=\ e^{ln \left(\lim \limits_{n \to \infty} \left(1+\frac{1}{n} \right)^n \right) }\\
&=e^{\left(\lim \limits_{n\to\infty}\ln\left(\left(1+\frac{1}{n}\right)^n\right)\right)} \end{split}

对 $\lim \limits_{n\to\infty} ln \left(1+ \frac{1}{n}\right)^n$ 来说：
$$ \lim_{n\to\infty}\ln\left(\left(1+\frac{1}{n}\right)^n\right)=\lim_{n\to\infty}n\cdot\ln\left(1+\frac{1}{n}\right) $$
令 $\Delta x = \frac{1}{n}$，可以看出来的是当 $n\to\infty$ 时，$\Delta x \to 0$。因此上式可以改写为：

\begin{split} \lim_{n\to\infty}n\cdot\ln\left(1+\frac{1}{n}\right) &=\lim_{\Delta x\to 0} \frac{ln\left(1+\Delta x\right)}{\Delta x}\\
&=\lim_{\Delta x\to 0} \frac{ln\left(1+\Delta x\right) + ln(1)}{\Delta x}\\
&=\left. \frac {d}{dx}ln(x) \right|_{x=1}\\
&= 1 \end{split}

所以有：

$$ \begin{split} \lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n = e^1 = e \end{split} $$

附：常用反三角函数求导公式

$\displaystyle \frac{d}{dx} \arcsin x = \displaystyle \frac{1}{\sqrt {1-x^2}}$
$\displaystyle \frac{d}{dx} \arccos x = \displaystyle -\frac{1}{\sqrt {1-x^2}}$
$\displaystyle \frac{d}{dx} \arctan x = \displaystyle \frac{1}{\sqrt {1+x^2}}$

What & How & Why

[ About ]

[ My Links ]

[ Notice ]

页面工具

站点工具

用户工具

目录