MITx: 18.01.2x Calculus 1B notes

首先思考一下，如何求下图中两个函数图像之间包裹的面积？


解决方案是使用黎曼和的方法来近似：

1. 首先进行 $x$ 上的细分，即 $dx$；将 $dx$ 视作长方形的底
2. 其次求出对应的 $y$ 作为高。可以观察到的是，此时的高是两个函数在 $x$ 时的差，即 $f(x)-g(x)$

因此，整个问题就可以转化为求定积分的问题，也就是：

$$ Area = \int_a^b(f(x)-g(x))dx $$ 其中 $[a,b]$ 为指定的 $x$ 上的区间。

来看一下例子：求 $x=y^2$ 与 $y=x-2$ 之间的面积。

为了更直观的理解我们需要求的面积，第一步通常会先做出图：




通过作图可以判断出我们要求的面积是图中紫色的部分；接下来需要求高的表达式，即之前提到的 $f(x)-g(x)$。通过观察：

• $f(x)$ 的表达式是 $x=y^2$ 在 $x$ 轴的上方部分，即 $y=\sqrt{x}$
• $g(x)$ 的表达是则有些复杂。可以观察到，在 $x=y^2$ 与 $y=x-2$ 两个函数的 $x$ 轴下方的交界处，$g(x)$ 发生了变化。交接点左边是 $y=-\sqrt{x}$ 的一部分，而右边是 $y=x-2$ 的一部分。显然 $g(x)$ 是一个分段函数，因此需要分段对高进行讨论。

为了明确分段的范围，我们需要求出该面积在 $x$ 轴上的起点和终点，以及 $g(x)$ 分段的分界点。可以看出来的是：

• 起点 $A$ 是原点
• 终点 $B$ 与分界点 $C$，实际上是函数 $x=y^2$ 与 $y=x-2$ 的两个交点。

令 $x=y^2$ 与 $y=x-2$ 相等，可得：

\begin{align} &y^2-y-2 = 0 \\ \Rightarrow &(y+1)(y-2)=0\\ \Rightarrow &y=-1 \,\,or\,\,y=2 \end{align}
将 $y=2$ 带入 $x=y^2$，$y=-1$ 带入 $y=x-2$，即可得到 $B$ 点坐标 $(4,2)$，$C$ 点坐标 $(1,-1)$。因此，$g(x)$ 的表达式可以确认为：

$$ \begin{cases} y=-\sqrt{x} \,\,\, 0<x\leq1\\ y=x-2\,\,\, 1<x\leq 4 \end{cases} $$
接下来只需要按照之前提到过的形式分段建立定积分进行计算即可，即：

$$ Area =\underbrace{ \int_0^1({\color{Red} \sqrt{x} }-(-{\color{Violet} \sqrt{x}} ))dx}_{left}+\underbrace{\int_1^4({\color{Red} \sqrt{x}} -({\color{Blue} x-2} ))dx}_{right} $$

上后面的例子可以用另外一种方法来解决。如果将 $y$ 作为细分的对象，很容易发现积分函数的上部和下部都是完整的，不用讨论分段的情况了。这种情况下，只需要将 $f(x)$ 与 $g(x)$ 转换为以 $y$ 为自变量的函数即可，即：

$$ Area = \int_{ya}^{yb}(g^{-1}(y)-(f^{-1}(y))dy $$

使用定积分求体积的思想也是基于黎曼和的。相比起 2D 面积，体积赋予被积函数（integrand）面积的意义，而细分的 $dx$ 则被视作高的细分。因此，求体积的过程实际上被视作了求以面积 $A(x)$ 为底，$dx$ 为高的“片”的黎曼和。表现为定积分形式即：

$$ V = \int A(x) \, dx $$
之后讨论的几种方法，都是基于以上理论的，针对于不同类型体积的具体方案。

某一类的体积可以被视作是多个圆盘体积的累积和，其函数在 $2D$ 空间上一般表现为抛物线：

这种情况下：

• 在 $x$ 处的$y$ 的值，为圆盘底面积的半径
• $dx$ 为圆盘底的厚度

因此每一片切片的体积可以表示为：

$$ Dv = \pi y^2dx $$
假设 $x$ 的范围是 $(a,b)$，且$y=f(x)$；那么该体积可以表示为：
$$ V= \int_a^b \pi (f(x))^2dx $$

该方法是体积求法的第二种变形。相较将单位体积视作 disk，该方法将单位体积视作 shell，而整个体积被视作多个 shell 的黎曼和：




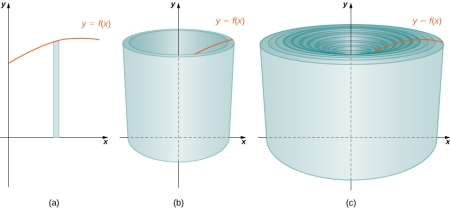
来看看该单位体积的表达式是如何建立的。首先细分的对象还是 $dx$。但与 disk 方法不同的是，此处的底面积变成了 $dx$ 与 $f(x)$ 的乘积：



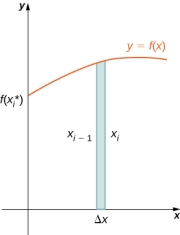
之所以这么处理，是因为在这种方法中，我们设想单位体积的形成是该底面绕 $y$ 轴一周形成的空心圆柱体。而该体积如果展开，就可以视作一个长方体，其长边即为底面旋转一周的周长：



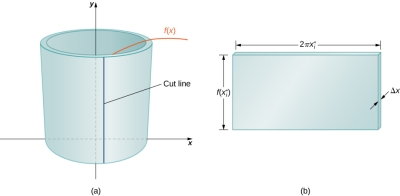
那么到此单位体积的计算方式已经非常清楚了：

$$ Dv = 2\pi x\cdot f(x) \cdot dx $$

假设 $x$ 的范围是 $(a,b)$，则总体积可以表示为：
$$ V = \int_a^b 2 \pi x f(x)dx$$
本节图片来源：lumen

以课程中的案例为例，其得到的计算公式为：

$$ V = \frac{\pi}{2}a^2 $$ $a$ 代表整个体积的高。此时我们希望利用该公式计算具体的体积，并将得到的结果用升表示。 当 $a$ 的单位是 $cm$ 时，令 $a=100cm$：

$$ V = \frac{\pi}{2}a^2 = \frac{\pi}{2} \cdot (100)^2 cm^3 = 5 \pi \cdot 1000cm^3 = 5 \pi L $$
当我们将 $a$ 的单位换成 $m$：
$$V = \frac{\pi}{2}a^2 = \frac{\pi}{2} \cdot 1^2 m^3 = \frac{\pi}{2}m^3 = \frac{\pi}{2}(100cm)^3 = 5000 \pi L $$
我们发现，使用不同的单位以后，公式计算出来的结果竟然完全不同了。这是因为积分中的上下极限是基于 $a$ 计算出来的。以本例中的 $a$ 为例：按 $y=x^2$ 计算 $x$ 的右极限，如果使用的是 $100cm$，那么计算出来的就是 $10cm$；如果使用的是 $1m$，那么计算出来的是 $1m$。这导致了定积分的范围变化了 10 倍，因此计算出来的结果肯定不会一样。

从结果上来说，两种情况都是正确的，因为 $f(x)$ 根据单位的不同被诠释成了不一样的函数关系。但实际情况下，我们需要赋予每个推导步骤实际的单位来获取正确的结果。不带单位的，推导出来的公式，是正确的，但给出的结果是取决于单位的，是破坏了标度无关性的（scaling violation）。

该方法基于 disk 方法，用于计算两个函数围成的不规则面积进行旋转后得到的体积。其核心思想是分别计算出两个部分的单位体积，用两个单位体积之差进行积分，就能得到最终的体积。比如下面的例子：求 $y=x^2$ 与 $y=x$ 围成的面积绕 $x$ 轴旋转的体积。



该问题实际上是在求 $y=x$ 和 $y=x^2$ 旋转之间的部分的差：

现在对两个体积分别使用 disk 方法，求出单位体积：

• $Dv_{y=x} = \pi x^2$
• $Dv_{y=x^2} = \pi x^4$

然后直接对其单位体积的差求积分即可：
$$ V= \int_0^1 \pi (x^2-x^4)dx $$ 该方法的流程与 2D 中求两个函数之间的面积极为类似。

离散型的平均值类型分为：

• 平均值（mean）：所有数的和除以个数
• 中位数（median）：有序数列中处于中间位置的数的值
• 众数（mode）：出现频率最高的数

与积分相关的是 mean。在几何意义上，定积分的平均值被定义为平均单位面积。也就是说，定积分的平均值与区间的乘积，等于该定积分表示的面积，即：

$$ ave(f)=\frac{1}{b-a}\int_a^bf(x)dx $$

假设 $f(x)$ 在 $[a,b]$ 上连续。如果将 $[a,b]$ 细分为 $n$ 份，那么每一份的大小为： $$ \Delta x=\frac{b-a}{n} $$ 根据黎曼和与定积分的关系，当无线细分，也就是 Delta x 趋近于 $0$，该黎曼和等于定积分： $$ \displaystyle \sum_{}f(x)\frac{b-a}{n}=\int_a^bf(x)dx $$ 此时对两边同时除以区间长度 $b-a$，得： $$ \displaystyle \sum_{}\frac{f(x)}{n}=\frac{1}{b-a}\int_a^bf(x)dx $$ 左边是平均值的定义，右边是连续型平均值的公式，至此连续性平均值与定积分关联了起来。

带权平均值即将数值以及对应的单位数相乘，再求和得到总体值，在除以总的单位数而得到的平均值。如果令数值为 $x_i$，对应的单位数（权，weight）为 $w_i$，那么带权平均值可以表示为：

$$ \frac{x_1w_1+x_2w_2+...+x_iw_i}{w_1+w_2+...w_i} $$
设 $f(x) = x$ 与 $w(x) = w$ 在 $[a,b]$ 上连续。如果将 $[a,b]$ 进行微分，那么每一份的值为：

$$ D_{weightSum} = f(x)w(x)dx $$ 在 $[a,b]$ 上的总体值则为： $$ \int_a^b f(x)w(x)dx $$ 同理，在 在 $[a,b]$ 上的总单位数为： $$ \int_a^b w(x)dx $$ 因此，带权平均值的定积分形式可以表示为：

$$ \frac{\int_a^b f(x)w(x)dx}{\int_a^b w(x)dx } $$

重心（center of mass）是带权平均值的应用。重心指的是一个可以使物体处于平衡状态的位置，是基于位置与重量的带权平均值。

一维重心的求解是求基于位置（此处为长度）与质量的带权平均值，即： $$ \displaystyle \bar{x} = \frac{\int _0^ L x \lambda (x)\, dx}{\int _0^ L \lambda (x)\, dx}. $$ 从单位上来讲：

• 分子的单位为 $Len \cdot Mass/Len \cdot Len = M \cdot L$
• 分母的单位为 $Mass/Len \cdot Len = M$

因此最终得到的结果单位为长度 $L$，也就是重心所处整个一维轴上的位置。

二维重心是一维重心的扩展。二维重心可以被视作使得某个带质量的面积平衡的的点。求解二维重心可以将 $x,y$ 轴上的一维重心分别求出，最后得到一个二维的坐标即为该面积的重心。该重心也被称为 Centorid，也就是质量基于面积的带权平均值。

求解需要分别求出 $x,y$ 上的重心： \begin{eqnarray} \displaystyle \bar{x}\displaystyle = \frac{\int _ a^ b x \, dA}{\int _ a^ b dA} \displaystyle \qquad dA = y\, dx\\ \displaystyle \displaystyle \bar{y} = \frac{\int _ a^ b y\, dA}{\int _ a^ b dA}\displaystyle \qquad dA = x\, dy \end{eqnarray}

这里的面积 $dA$ 需要根据细分的对象来表示。

假设有一个盛满水的锅。锅高 $1m$，其形状满足 $y = x^2$ 曲线。现对其进行加热，已知其底部的水温为 $100C$，如果希望其顶部（开口处）的水温达到 $70C$，需要多少能量？平均水温是多少？



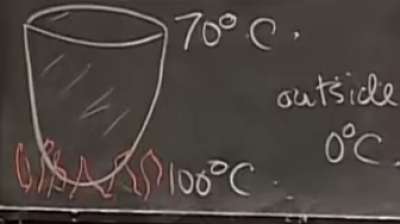
对于第一个问题，首先可以明确我们需要什么样的信息。能量可以通过体积与温度的乘积来表示： $$ \displaystyle \underbrace{\text {Heat energy}}_{\text {cal}} = \underbrace{\text {(Volume)}}_{\text {mL}} \cdot \underbrace{\text {(Temperature)}}_{{}^{\circ {}} \text {Celsius}}. $$ 因此只需要找出体积与温度的表达式就可以。根据 method of disk，以 $y$ 轴做细分，那么每一层的细分的体积为： $$ \pi x^2 \, dy $$ 根据温度与 $y$ 轴的关系，可知当前 $y$ 处的温度为： $$ T = 100-30y $$

因此，达到底部 $100C$，顶部 $70C$ 水温需要的总能量为： $$ \int _0^1 \left(100-30y\right)\cdot \pi y\, dy $$

接下来需要求平均温度。由前面可知，能量可以表示为体积与温度的乘积。根据单位，可以判断出平均温度是基于温度与体积的带权平均值，因此只需要使用总的能量除以总的体积即可得到平均温度值，即： $$ \displaystyle \frac{\int _0^1 T\cdot \pi y \, dy}{\int _0^1 \pi y \, dy} $$