LAFF Week 1 Notes

本章的一个核心概念是，某些对 Vector 的操作都可以被称之为一个 Vector Function。Vector Function 与我们正常接触的函数一样，有输入也有输出。它输入向量（可能夹杂着标量），得到一个新的向量。换句话说，这种 Vector Function 完成了 一个向量到另外一个向量的转化 （map a vector to vector）。理解这个点非常重要，这是第二章理解线性变换和矩阵的基础。

• 代数上：一个标量与一个矢量的每一个分量相乘，得到新的向量
• 几何上：向量的缩放

$$ ax = \begin{pmatrix} ax_{0}\\ ax_{1}\\ \vdots\\ ax_{n} \end{pmatrix} $$

• 代数上：两个向量的对应分量相加，得到新的向量
• 几何上：三角形法则

$$ x+y = \begin{pmatrix} x_{0}+y_{0}\\ x_{1}+y_{1}\\ \vdots\\ x_{n-1}+y_{n-1}\\ \end{pmatrix} $$ 向量的加法规则同样适用于向量的减法。

$ax+y$，即一个标量乘上一个向量，再加上另外一个向量的运算；也就是向量的缩放与相加的复合运算。

$$ ax+y = \begin{pmatrix} ax_{0}+y_{0}\\ ax_{1}+y_{1}\\ \vdots\\ ax_{n-1}+y_{n-1}\\ \end{pmatrix} $$

Dot product / 点积是本章的一个比较重要的概念。

点积通常表示为：

$$dot(x,y) = x^Ty$$ 这是因为在代数上人们习惯于在形式上将点积写成一个行向量与与一个列向量相乘，而在线性代数中默认的向量都是列向量，因此实际上这个写法就是在告诉我们，这是我们习惯上的点积的形式，即： $$ \begin{pmatrix} x_{0}\\ x_{1}\\ \vdots\\ x_{n} \end{pmatrix}^T \begin{pmatrix} y_{0}\\ y_{1}\\ \vdots\\ y_{n} \end{pmatrix} = \begin{pmatrix} x_{0} x_{1} \cdots x_{n} \end{pmatrix} \begin{pmatrix} y_{0}\\ y_{1}\\ \vdots\\ y_{n} \end{pmatrix} $$

点积的代数意义是将两个向量对应分量相乘，再将所有相乘的结果相加，最终得到一个标量，即： $$x^Ty = x_{0}y_{0}+x_{1}y_{1}\cdots x_{n-1}y_{n-1}$$

点积的几何意义是与向量的（欧式）长度相关的，放到之后的向量长度一起讨论。

向量的长度在几何上指的是向量在欧式空间中的长度，而在代数上表现为分量的平方之和再开方得到的结果，即： $$||x||_2 = \sqrt{\sum_{i=0}^{n-1}Xi^2}$$

而有趣的是，我们将根号中间的内容展开，得到的是： $$x_0x_0+x_1x_1 \cdots x_{n-1}x_{n-1}$$ 这不正好是向量 $x$ 与其自身的点积表达式吗？因此，向量的长度在代数上可以写成另外一种形式，即： $$||x||_2 = \sqrt{x^Tx}$$

先来看看一张图：



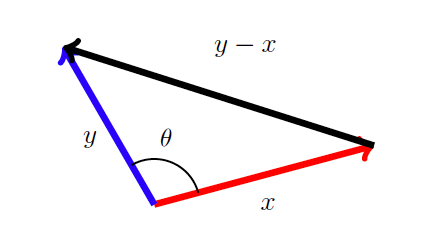
图片来源：LAFF课件

针对这种二维空间中的向量长度，我们在高中学过一个公式，即：
$$cos \theta = \frac{x^T y}{(\| x \| _2 \| y \| _2)}$$

来看看这个是怎么推导来的。对于三角形来说，我们有一个定理称为余弦定理。因为余弦定理中所有的边都是标量，因此我们用向量的长度来表示每个边。按上图的向量，我们将余弦定理写出来，即：
$$||y-x||^2_2 = ||x||^2_2+||y||^2_2-2||x||_2||y||_2cos\theta$$

通过之前的点积与向量长度的公式，上述式子可以写成：
$$y^Ty -2x^Ty +x^Tx = x^Tx + y^Ty - 2||x||_2||y||_2cos\theta$$

化简一下上式就能得到之前提到的公式。

不仅如此，点积还有一个妙用：我们通过计算发现，在两个向量正交（几何上垂直）的时候，$x^T y = 0$。以此为分界线，点积的正负可以判断 $\theta$ 的大小；而通过这个性质，我们可以用点积来判断两个向量之间的关系如何。

Vector Addition:

• $x+y = y+x$, commutative
• $(x+y)+z = x+(y+z) $, associative
• $x + 0 = x$
• $-x + x = 0$

Dot product:

• $x^Ty = y^Tx$, commutative
• $x^T(y+z)=x^Ty+x^Tz$, Distributes over vector addition
• $(x+y)^Tz=x^Tz+y^Tz$
• $(x+y)^T(x+y)=x^Tx+2x^Ty+y^Ty$
• $x^Ty=0$ 意味着 $x,y$ 正交
• $cos(\theta) = \frac{x^Ty}{||x||_2||y||_2}$
• For $x\in R^n, x^Te_i=e_i^Tx=\chi_i$

Slicing and Dicing 指的就是将向量或者矩阵划分为更小的子向量与子矩阵。该操作的更多的意义在于方便设计向量和矩阵的某些运算算法；通过 Slicing and Dicing 我们可以将某个向量或矩阵的运算分解为更小的运算的单位，从而方便写成迭代的模式。

一个比较重要的性质：

$$x^Ty = \left( \frac{x_0}{x_1}\right)^T\left(\frac{y_0}{y_1} \right) = x_0^Ty_0 + x_1^Ty_1$$

其中的 $x_1$、$y_1$ 是 $x、y$ 的子向量，也就是说，两个向量的点积等于其子向量的点积之和。

• 本章所有操作算法 matlab文件