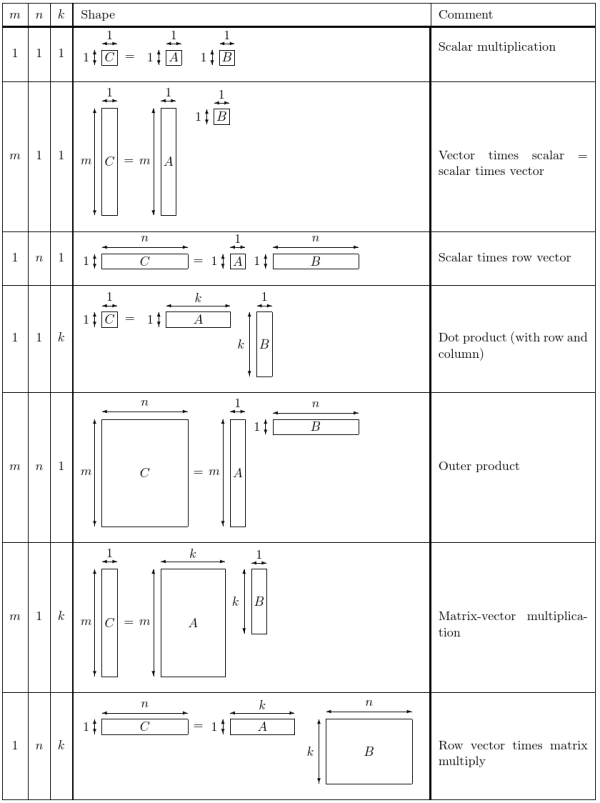
目录
Matrix-Vector to Matrix-Matrix Multiplication
LAFF Week 4 Notes
本章的核心概念主要介绍了如何对矩阵和向量的乘法进行象限分割,并利用这种象限分割优化特定矩阵与向量的乘法的算法。除此之外另外一个比较重要的内容是如何从矩阵向量乘法的角度去解释矩阵与矩阵的乘法。
矩阵向量乘法的象限分割
通过第三章,我们得知矩阵可以使用象限分割的方法来分割矩阵;同时,我们也知道通过对行或者列进行优先分割,我们可以将矩阵的乘法用点积或者 AXPY 的方式进行计算。那有没有办法将这两者联系到一起呢?来看看下面的修改:
对 A, x, y 进行分割
我们知道在矩阵向量乘法中,每次迭代的最终结果都会加到对应的 $y$ 的分量上,无论是哪一种方式来计算。想象一下之前的象限分割下的各种算法,每一次迭代中 $y$ 的分量作为结果,都是有对应区域的 $A$ 与 $x$ 的分量产生的。因此,我们可以认为在分割向量乘法中,$A$、$x$、$y$ 中的元素是一一对应的。那么我们很容易得出一个结论: $$ \displaystyle \left( \begin{array}{ c | c | c | c } A_{0,0} & A_{0,1} & \cdots & A_{0,N-1} \\ \hline A_{1,0} & A_{1,1} & \cdots & A_{1,N-1} \\ \hline \vdots & \vdots & \ddots & \vdots \\ \hline A_{M-1,0} & A_{M-1,1} & \cdots & A_{M-1,N-1} \end{array} \right) \left( \begin{array}{ c } x_0 \\ \hline x_1 \\ \hline \vdots \\ \hline x_{N-1} \end{array} \right) \\ = \left( \begin{array}{c c c} A_{0,0} x_{0} + A_{0,1} x_{1} + \cdots + A_{0,N-1} x_{N-1} \\ \hline A_{1,0} x_{0} + A_{1,1} x_{1} + \cdots + A_{1,N-1} x_{N-1} \\ \hline \vdots \\ \hline A_{M-1,0} x_{0} + A_{M-1,1} x_{1} + \cdots + A_{M-1,N-1} x_{N-1} \end{array} \right) $$
象限分割下的矩阵向量乘法
点积观点的算法改写
点击观点的算法在一般情况下是行优先的算法,总的来说就是 $A$ 的每一行作为一个整体与 $x$ 做点积,得到的值加到 $y$ 对应分量上。经过象限分割后,我们的三个变量发生一定的变化:
- $A$ 的行从整体到被分割成三部分(从左到右)
- $x$ 从整体到被分割成三部分(从上到下)
- $y$ 保持状态不变(之前的算法中就被分割了)
那么算法的变动实际上就很清楚了,请参考下图:
<html>
<img src=“/_media/math/linear_algebra/laff/q_M_dot.svg” width=“500”>
</html>
那么实际上,每次迭代中的变动如下:
y1 = a1t * x + y1 // M mult V via dot
y1 = a10t * x1 + a11 * chi1 + a12t * x2 + y1; //M mult V via dot in quadrantsAXPY观点的算法改写
AXPY 观点下的矩阵向量乘法是列优先的,也就是用 $x$ 的分量来乘以对应矩阵的列,再将结果加到整个 $y$ 上。我们也来看看经过象限分割后,三个变量发生了什么样的变化:
- $A$ 在行中也有分割,因此之前作为单位的列分割成了三部分 ((a01, a11,a21)t)
- $x$ 之前就有从上到下的分割,保持原样
- $y$ 不再是一个整体,而是从上到下分割成了三部分((y0, psi,y2)t)
算法的变动可以参考下图:
<html>
<img src=“/_media/math/linear_algebra/laff/q_M_AXPY.svg” width=“300”>
</html>
实际上的算法变动为:
y = chi * a1 + y; //M mult V via AXPY
//--M mult V via AXPY in quadrants---//
y1 = chi * a01 + y1;
psi = chi * a11 + psi;
y2 = chi * a21 + y2;Transposing a Partitioned Matrix
对分割后的矩阵转置分二步:
- 按区域为单位,对整个矩阵进行转置。区域内部的不转置
- 对区域内部的单位分别进行转置。
特殊矩阵与矩阵向量乘法
转置矩阵的矩阵向量乘法
假设我们要求 $y = A^Tx +y$。通常情况下,我们会先求 $A$ 的转置矩阵,再与 $x$ 相乘,最后累加到 $y$ 上。然而,在计算机中,如果我们有了转置的中间步骤,我们就需要找一块空间来存储 $A$ 的转置结果;更坏的是,为了转置 $A$,我们很可能需要遍历整个矩阵 $A$。因此,我们需要设计一种算法来避免这些情况的发生,该算法的核心就是避免转置操作的发生。
实际上,不管是通过点积观点还是AXPY观点,我们都会发现一个现象:那就是原矩阵的列就是转置矩阵的行,原矩阵的行就是转置矩阵的列。因此,我们只需要通过点积运算,就可以将当前的行(列)作为列(行)进行运算,即:
- 如果是点积观点的乘法,那么是行优先,那么需要按列划分 $A$, 然后做 $x$ 与 $A$ 中列的点积,即$A_1^Tx$;
- 如果是AXPY观点的乘法,那么是列优先,那么只需要按行划分 $A$,然后做 $x$ 与 $A$ 中行的AXPY 操作,即 $A_1x$(因为按行划分,因此原有的行为 $A_1^T$)。
三角矩阵与矩阵向量乘法
三角矩阵是一个很比较特殊的存在。在三角矩阵中,有一半的元素都是 0,而 0 意味着我们没有必要在这些 0 元素上浪费时间进行计算。因此在设计算法的时候,我们必须要考虑如何使用迭代将 0 的区域划分出来,并舍弃这一部分本应存在于一般矩阵与向量的乘法中的运算。
从点积角度来看
上三角矩阵:
以上三角矩阵为例,我们来看一看在正常的点积矩阵向量乘法中,属于上三角矩阵的 0 会在每一次迭代中处于什么样的位置:
<html>
<img src=“/_media/math/linear_algebra/laff/m_m_v_tr.svg” width=“400”>
</html>
以上图为例($U$ 为上三角矩阵的简称),可以看到的是,每一次迭代中, $U_{10}^T$ 都是 $U$ 中元素为 0 的区域,因此这部分的运算对于一般的矩阵向量乘法来说是不必要的,可以删去:
y1 = a10t * x1 + a11 * chi1 + a12t * x2 + y1; //M mult V via dot in quadrants
y1 = u11 * chi1 + u12t * x2 +y1; //U mult V via dot in quadrants反过来看,如果是下三角矩阵,则是 $L_{12}^T$ 的部分在每次迭代中(图中绿色的区域)都为 0,因此下三角矩阵只需要将 $L_{10}^T$ 的运算部分去掉即可:
y1 = a10t * x1 + a11 * chi1 + a12t * x2 + y1; //M mult V via dot in quadrants
y1 = l10t * x1 + l11 * chi1 +y1; //L mult V via dot in quadrants那么对角线为 0,只需要将迭代中的对角线部分($A_{11}$)去掉就好。
x = Ux:
以上是求 $y = Ax +y$ 的情况。再来看看 $x = Ux$ 的情况,这种情况下输入和输出的都是 $x$。那么意味着:
chi1是每次迭代会被覆盖数据的那个分量。chi1会参与其中的一次运算(点积的一部分)
因此我们需要注意的是在 chi1 被覆盖之前,先让其参与点积的运算,于是就有:
chi1 = u11 * chi1; // compute dot with original chi1, then overwrite it
chi1 = u12t * x2 + chi1;不过这里又会出现一个问题:上面的做法对于上三角矩阵是没有问题的;但对于下三角矩阵来说就会出问题了:对于下三角矩阵,舍去的是 $L_{12}^T$ 部分,$L_{10}^T$ 是需要先被计算的(遍历的顺序)。但我们不能将其存到
chi1 里,因为我们接下来还要对 $U_{11}\chi_1$ 进行计算,如果覆盖了 chi1,那么接下来的结果就不正确了。那应该怎么办呢?
很简单,我们只需要将其作为一个 “上三角矩阵” 来处理就可以了;也就是说,我们可以从右下角开始我们的遍历,这样之前的 $L_{10}^T$ 就变成了 “$L_{12}^T$” 了,计算的第一位就变成了 $L_{11} \chi_1$ 了。 因此 $x = Lx$ 可以写成:
chi1 = u11 * chi1; // compute dot with original chi1, then overwrite it
chi1 = u10t * x0 + chi1; //这里的u10t / x0 都是从右下方开始计数的,因此遍历位置处于 u11 的后面y = U^Tx + y:
除了以上情况,在象限分割下我们也能更好的处理转置矩阵与向量的乘法。我们知道在点积观点下进行转置矩阵的运算都是将行看成列然后与 $x$ 进行点积的;鉴于上三角矩阵对角线下方都是 0,那么只需要对对角线元素 $U_{11}$ 与对角线上方元素 $U_{01}$ 与对应 $x$ 分量进行点积就可以了:
psi1 = laff_dots(upsilon11, chi1, psi1);
psi1 = laff_dots(u01, x0, psi1);注意:该运算与 $x=Ux$ 不同。转置矩阵乘法使用列与 $x$ 做点积,如果从左上方开始遍历,那么县运算会是 $U_{01}$。由于 $U_{01}$ 的运算会覆盖 $\chi_1$ 的结果,因此会导致 $\chi_1$ 的值错误。所以该运算需要从右下角开始遍历(正好与 $x=Ux$ 相反)
chi1 = laff_dot(upsilon11, chi1);
chi1 = laff_dots(u01, x0, chi1); // 这里的 u01 实际上是 u01t,但laff_dots支持u01到u01t的点积转换。该运算与向量的乘法与之前类似:只需要把
l01 替换成 l21 就可以了:
/*y = L^Tx + y*/
psi1 = laff_dots(lambda11, chi1, psi1);
psi1 = laff_dots(l21, x2, psi1); % l21t in the algorithm but OK for laff_dots()
/*x = L^Tx*/
chi1 = laff_dot(lambda11, chi1);
chi1 = laff_dots(l21, x2, chi1);从AXPY角度来看
还是从上三角矩阵谈起。先来看看在 AXPY 算法的迭代中,0 都处于哪些区域:
<html>
<img src=“/_media/math/linear_algebra/laff/m_m_v_tr_axpy.svg” width=“300”>
</html>
上三角矩阵:
对于上三角矩阵来说, $U_{21}$ 区域的元素全为 0,因此可以去掉。因此将一般情况下 AXPY 象限分割算法应用到上三角矩阵中,迭代部分就可以改写为:
y0 = u01 * chi1 +y0;
psi1 = u11 * chi1 +psi1;下三角矩阵需要去掉的部分为图中所有绿色的部分,也就是 $L_{01}$ 的部分。因此算法可以改写为:
psi1 = l11 * chi1 +psi1;
y2 = l21 * chi1 +y2;只需去掉
u11/l11 部分即可。
x = Ux: 对于 AXPY 的迭代部分,
chi1 是需要保证在所有运算结束之前不变的。不过在该运算中,采用左上开始的遍历进行运算,并不会在运算结束之前改变 chi1 的值。
x0 = chi1 * u01 + x0;
chi1 = chi1 * u11;这个运算与点积观点下的运算类似。如果从左上开始,
chi1 与 l11 的运算会改变 chi1 本身的值,造成后面的运算出错。因此我们从左下开始遍历,将整个运算换成了上三角矩阵的运算,也就是下三角矩阵里的 l21 编程了 上三角矩阵里的 l01:
x2 = chi1 * l21 +x2;
chi1 = l11 * chi1;AXPY观点下的乘法只需要将列视作行进行 AXPY 操作,就可以得到转置矩阵与向量相乘一样的结果了。分别来看看算法的改动:
y = U^Tx + y:
之前参与运算的区域是 $U_{01}$,那么对应的转置区域就是 $U_{12}^T$。
psi1 = laff_axpy(chi1, upsilon11, psi1);
y2 = laff_axpy(chi1, u12t, y2);y0 = laff_axpy(chi1, l10t, y0); // l10 in the algorithm but OK for laff_axpy()
psi1 = laff_axpy(chi1, lambda11, psi1);与点积观点的乘法类似,因为需要先算
u12t 再算 u11,因此必须从右下角开始遍历才能保证 u12t 在 u11 区域之前计算:
x2 = laff_axpy(chi1, u12t, x2); // u12 in the algorithm but OK for laff_dots()
chi1 = laff_axpy(chi1, upsilon11, 0);同样与点积观点类似,先算
u10t 再算 u11,从左上角开始遍历正好可以满足该顺序。
y0 = laff_axpy(chi1, l10t, y0); // l10 in the algorithm but OK for laff_axpy()
psi1 = laff_axpy(chi1, lambda11, psi1);对称矩阵与矩阵向量乘法
对称矩阵的元素相对于主对角线对称,因此在对阵矩阵与向量的乘法中,我们只需要利用一半的矩阵空间就可以表达整个对称矩阵,并提供足够的信息完成运算。
实现该算法实际上非常简单,只需要利用转置矩阵就可以。通过转置某一个区域,我们能用一个区域存储的内容表达两个区域的内容。下面来看看矩阵内容存储在下部和上部分别需要置换哪些区域:
内容在下部
点积观点:
内容在下部,意味着 $A_{12}^T$ 区域的内容在对角线以上,替换成 $A_{21}$ 即可:
psi1 = laff_dots( a10t, x0, psi1 );
psi1 = laff_dots( alpha11, chi1, psi1 );
psi1 = laff_dots( a21, x2, psi1 );内容在下部,意味着 $A_{01}$ 区域的内容在对角线以上,替换成 $A_{10}^T$ 即可:
y0 = laff_axpy( chi1, a10t, y0 );
psi1 = laff_axpy( chi1, alpha11, psi1 );
y2 = laff_axpy( chi1, a21, y2 );内容在上部
点积观点: 内容在下部,意味着 $A_{10}^T$ 区域的内容在对角线以下,替换成 $A_{01}$ 即可:
psi1 = laff_dots( a01, x0, psi1 );
psi1 = laff_dots( alpha11, chi1, psi1 );
psi1 = laff_dots( a12t, x2, psi1 );内容在上部,意味着 $A_{21}$ 区域的内容在对角线以上,替换成 $A_{12}^T$ 即可:
y0 = laff_axpy( chi1, a01, y0 );
psi1 = laff_axpy( chi1, alpha11, psi1 );
y2 = laff_axpy( chi1, a12t, y2 );更效率的算法
矩阵在计算机中如果以列为单位存储,访问起来会更加快速(计算机中内存单元就是以列为单位存储的)。来看看如何实现该算法:
- 假设 $A$ 是对称矩阵,那么 $A$ 可以由两个三角矩阵组成,记做$A = L + \hat{L}^T$
- 令 $L$ 为下三角矩阵,$\hat{L}$ 为严格下三角矩阵。
此处还没有看明白,待完善。
Matrix-Matrix Multiplication
为什么会有矩阵乘法
先来看一个预测天气的例子:
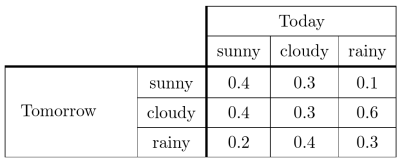
表中的元素是概率。行列的交界处的元素是对应今天的天气转变到对应的明天的天气的概率。假设我们要求明天是晴天的概率,那么我们就要考虑三种情况:今天是晴天或者阴天或者雨天的情况下,明天是晴天的概率,然后将其求和:
$$X_{sunny}^{tomo}=X_{sunny}^{today} *0.4 + X_{cloudy}^{today} *0.3 +X_{rainy}^{today} *0.1$$
因此整个明天的所有天气预报可以表示为一个向量:
$$
X_{sunny}^{tomo}=X_{sunny}^{today} *0.4 + X_{cloudy}^{today} *0.3 +X_{rainy}^{today} *0.1\\
X_{cloudy}^{tomo}=X_{sunny}^{today} *0.4 + X_{cloudy}^{today} *0.3 +X_{rainy}^{today} *0.6\\
X_{rainy}^{tomo}=X_{sunny}^{today} *0.2 + X_{cloudy}^{today} *0.4 +X_{rainy}^{today} *0.3
$$
那么再将其做一个推广,也就是 $k+1$ 天后的天气向量可以由 $k$ 天后的天气向量表示,即
$$
X_{sunny}^{k+1}=X_{sunny}^{k} *0.4 + X_{cloudy}^{k} *0.3 +X_{rainy}^{k} *0.1\\
X_{cloudy}^{k+1}=X_{sunny}^{k} *0.4 + X_{cloudy}^{k} *0.3 +X_{rainy}^{k} *0.6\\
X_{rainy}^{k+1}=X_{sunny}^{k} *0.2 + X_{cloudy}^{k} *0.4 +X_{rainy}^{k} *0.3
$$
上面的方程组是不是很熟悉?那么实际上将上面的式子转化为 $y = Ax$ 的形式就是:
$$
\begin{pmatrix}
X_{sunny}^{k+1}\\
X_{cloudy}^{k+1}\\
X_{rainy}^{k+1}
\end{pmatrix}
=
\begin{pmatrix}
0.4& 0.3 &0.1 \\
0.4& 0.3 &0.6 \\
0.2& 0.4 &0.3
\end{pmatrix}
\cdot
\begin{pmatrix}
X_{sunny}^k\\
X_{cloudy}^k\\
X_{rainy}^k
\end{pmatrix}
$$
那么再往前一步,如果我们要从 $k-1$ 天前推测 $k+1$ 天的天气,那么就应该有:
$$
\begin{pmatrix}
X_{sunny}^{k+1}\\
X_{cloudy}^{k+1}\\
X_{rainy}^{k+1}
\end{pmatrix}
=
\begin{pmatrix}
0.4& 0.3 &0.1 \\
0.4& 0.3 &0.6 \\
0.2& 0.4 &0.3
\end{pmatrix}
\cdot
\begin{pmatrix}
0.4& 0.3 &0.1 \\
0.4& 0.3 &0.6 \\
0.2& 0.4 &0.3
\end{pmatrix}
\cdot
\begin{pmatrix}
X_{sunny}^{k-1}\\
X_{cloudy}^{k-1}\\
X_{rainy}^{k-1}
\end{pmatrix}
$$
这里就出现了矩阵的乘法了!我们知道,矩阵就是映射。如果令当前表示天气概率的矩阵为 $A$, 令线性变换 $L(x+1) = Ax$。那么我们这里做的操作实际上就是:
$$L(k+1) = L(k) = L(L(k-1)) = AA(k-1))$$
从上式可以推断,矩阵的乘法类似于复合函数的用法,类似于 $ y=g(f(x))$ 一类的运算。
来看看矩阵乘法的正式定义:
$\text{Let }L_A:\Bbb{R}^k\to\Bbb{R}^m\text{ and }L_B:\Bbb{R}^n\to \Bbb{R}^k$ both be linear transformations and, for all $x\in \Bbb{R}^n$,define the function $L_C:\Bbb{R}^n\to \Bbb{R}^m\text{ by }L_C(x) = L_A(L_B(x))$. The operation that computes $C$ from $A$ and $B$ is called Matrix-matrix multiplication.
注意这个定义里有一个重点:
矩阵 $A$ 的映射是 k → m,因此矩阵 $A$ 应该是 m*k 的矩阵。同理,矩阵 $B$ 应该是 k*n 的矩阵。矩阵乘法要求矩阵 $A$ 的列数必须等于矩阵 $B$ 的行数,这样才能使整个矩阵乘法有意义(well-defined)。而 $A$、$B$ 两者相乘的结果 $C$ 是一个 m*n 的矩阵。
如何计算矩阵乘法
先从定义上来看如何计算结果 $C$。按照之前推导矩阵的手法我们可以将 $C$ 划分成以列为单位的很多向量 $C_0,C_1\cdots C_{n-1}$。用 unit basis vector 来表示第 $j$ 个向量,那就有: $$C_j =C_{e_j} = L_c(e_j)$$
又因为 $C$ 的列数等于 $B$ 的列数,因此:
$$L_c{e_j} = L_A(L_B(e_j)) = A(B_{e_j}) = AB_j$$
由此可见,矩阵的乘法实际上就是由一系列的矩阵向量乘法组成的。
接下来我们将这些矩阵中的第 $j$ 个列向量再进行细分,那么根据上面的式子有:
$$C_{i,j} = A^T_{i}B_j$$
那么实际上 $C_{i,j}$ 的值就等于 $A$ 的第 $i$ 行 与 $B$ 的第 $j$ 列的点积。那么归纳下来就是:
$$\begin{array}{c c} C = \left( \begin{array}{c c c c } \gamma _{0,0} & \gamma _{0,1} & \cdots & \gamma _{0,n-1} \\ \gamma _{1,0} & \gamma _{1,1} & \cdots & \gamma _{1,n-1} \\ \vdots & \vdots & \vdots & \vdots \\ \gamma _{m-1,0} & \gamma _{m-1,1} & \cdots & \gamma _{m-1,n-1} \\ \end{array} \right) , \quad A = \left( \begin{array}{c c c c } \alpha _{0,0} & \alpha _{0,1} & \cdots & \alpha _{0,k-1} \\ \alpha _{1,0} & \alpha _{1,1} & \cdots & \alpha _{1,k-1} \\ \vdots & \vdots & \vdots & \vdots \\ \alpha _{m-1,0} & \alpha _{m-1,1} & \cdots & \alpha _{m-1,k-1} \\ \end{array} \right), \\ \mbox{and} \quad B = \left( \begin{array}{c c c c } \beta _{0,0} & \beta _{0,1} & \cdots & \beta _{0,n-1} \\ \beta _{1,0} & \beta _{1,1} & \cdots & \beta _{1,n-1} \\ \vdots & \vdots & \vdots & \vdots \\ \beta _{k-1,0} & \beta _{k-1,1} & \cdots & \beta _{k-1,n-1} \\ \end{array} \right). \end{array}
$$
then $C = A B$ means that $\gamma _{i,j} = \sum _{p=0}^{k-1} \alpha _{i,p} \beta _{p,j}$
外积
跟点积相反,外积是一个列向量与一个行向量相乘,记做 $xy^T$。外积的计算如下:
$$xy^T = \displaystyle \left( \begin{array}{c} \chi _0 \\ \chi _1 \\ \vdots \\ \chi _{m-1} \end{array} \right) \left( \begin{array}{c} \psi _0 \\ \psi _1 \\ \vdots \\ \psi _{n-1} \end{array} \right)^ T = \left( \begin{array}{c} \chi _0 \\ \chi _1 \\ \vdots \\ \chi _{m-1} \end{array} \right) \left( \begin{array}{c c c c} \psi _0 & \psi _1 & \cdots & \psi _{n-1} \end{array} \right) \\=
\displaystyle \left( \begin{array}{c c c c} \chi _0 \psi _0 & \chi _0 \psi _1 & \cdots & \chi _0 \psi _{n-1} \\ \chi _1 \psi _0 & \chi _1 \psi _1 & \cdots & \chi _1 \psi _{n-1} \\ \vdots & \vdots & & \vdots \\ \chi _{m-1} \psi _0 & \chi _{m-1} \psi _1 & \cdots & \chi _{m-1} \psi _{n-1} \end{array} \right)$$
可以看出来的是,点积得到是标量,而外积得到的是一个矩阵。
用矩阵乘法描述之前的操作
参考资料
- 所有非 svg 图片均来自 LAFF 课件。