目录
Vector / 向量空间
所有 math 条目下的内容均以极不严谨的个人理解方式书写,请见谅!
除非特别标明,本笔记中所有图片版权属于马同学线性代数课程。
向量是什么?
向量是一个很古老的物理概念,用来表示物体的运动性质。它可以代表力,可以代表速度或者加速度等等,是一个具有方向与大小的几何对象。
随着科学的发展,科学家们试图从数学上去诠释向量。与物理的定义不同的是,数学家们需要找到一种更严谨的方式来定义向量。科学家们通过复数,找到一种方法来诠释向量:即将向量至于坐标系中,用坐标来讨论向量。
向量的表示
为了表示方向,我们在数学中始终遵循向量的起点在原点;正因如此,我们就可以用终点的坐标来表示整个向量。
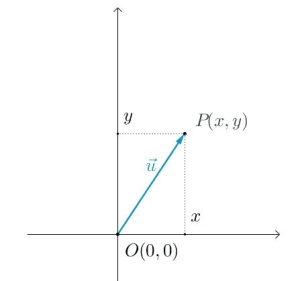
从上图我们可以看出,$P$ 点的坐标可以很好的表示向量。推广到整个坐标系,则可以发现向量与坐标系中的点形成了一一对应的关系。
$$\overrightarrow{u} = (x,y)$$
以上的几何解释显而易见的可以应用到三维坐标系中:
$$\overrightarrow{u} = (x,y,z)$$
需要注意的是,超过三维,就没有几何意义了。此时的向量更像是计算机中的数组。比如我们描述一个游戏角色的属性,可以通过一个向量来描述:
$$(生命,能量,攻击,防御....)$$
通过以上视角,我们可以整理出向量的定义:
$n$ 个有序的数 $a_1,a_2,...,a_n$ 所组成的数组称为 $n$ 维向量,这 $n$ 个数称为该向量的 $n$ 个分量,第 $i$ 个数 $a_i$ 称为第 $i$ 个分量。$n$ 维向量可写成一行,也可写成一列。分别称为行向量和列向量,比如:
$$\begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \\ .... \end{pmatrix} \tag{列向量}$$ $$(a_1,a_2,a_3,....) \tag{行向量}$$
向量的长度与方向
物理中的向量是有长度与方向的。
令一个向量 $\overrightarrow{u} = \overrightarrow{OP}$,其中$O$代表原点,$P$代表其终点,那么向量的长度就被记做 $||\overrightarrow{u}||$ 或者 $||\overrightarrow{OP}||$,其几何表示如下:
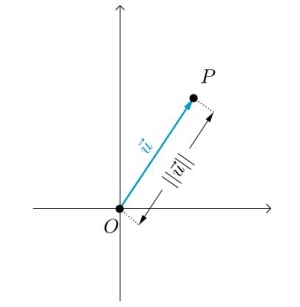
而其方向可以通过向量与坐标轴之间的夹角来表示:
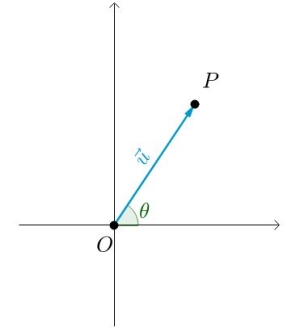
因为向量是有方向的,如果我们调换向量的起点与终点,那么得到的向量与原有的向量长度相同,方向向相反,即:
$$||\overrightarrow{AB}|| = ||\overrightarrow{BA}||$$
零向量
还有一种特殊的向量,被称为零向量,也就是起点与终点为同一个点的向量。零向量的长度为零,记做 $\overrightarrow{0}$
平行的向量
满足下列条件的向量平行:
- 两个具有相同或者相反方向的向量平行
- 零向量与任意向量平行
向量的基本操作
向量具有两种操作:加法与数乘。
向量的加法
向量加法的几何意义
我们在物理中学到的力的合成实际上就是向量的加法。向量的加法分成两步:
- 首先将两个向量首尾相连
- 再以原点为起点,连接平移后的向量,作出有向线段。
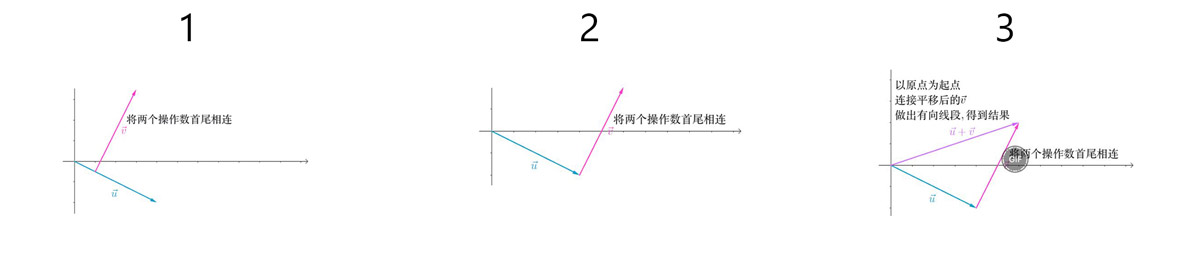
可以看到的是,图中的三个向量最后形成了一个三角形,因此我们将向量的加法又称为三角形法则。三角形法则也同样适应于三维空间中。
向量加法的代数意义
以列向量为例,设:
$$\vec{a} = \begin{pmatrix}
a_{1}\\
a_{2}\\
a_{3} \\
... \\
a_{n}
\end{pmatrix},
\vec{b} = \begin{pmatrix}
b_{1}\\
b_{2}\\
b_{3} \\
... \\
b_{n}
\end{pmatrix}
$$
则 $\vec{a}+\vec{b}$ 的结果定义为:
$$\vec{a}+\vec{b}= \begin{pmatrix}
a_{1}\\
a_{2}\\
a_{3} \\
... \\
a_{n}
\end{pmatrix}+
\begin{pmatrix}
b_{1}\\
b_{2}\\
b_{3} \\
... \\
b_{n}
\end{pmatrix} =
\begin{pmatrix}
a_{1}+b_{1}\\
a_{2}+b_{2}\\
a_{3}+b_{3} \\
... \\
a_{n}+b_{n}
\end{pmatrix}
$$
可以看出来,向量相加的过程就是对应的分量相加的过程。如果反映到几何中,就是按照分量一步一步的平移,这与之前提到的三角形法则是符合的。
根据三角形法则,与三角形的定义,我们可以直接得出一个结论:
$$|\vec{u}|+|\vec{v}| \geq ||\vec{u}+\vec{v}||$$
当$\vec{u}、\vec{v}$ 共线的时候取等号。
向量的数乘
向量允许自身与一个实数进行相乘的运算,我们称之为向量的数乘。
向量数乘的几何意义
令 $k \in \mathbb{R}$,则 $k\overrightarrow{u}$ 的结果可以表示为如下图:
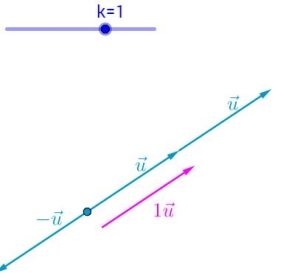
可以看出来,向量数乘的几何意义为缩放,其中:
- $|k|$ 为缩放比例(系数)
- $k$ 本身的正负决定缩放后的向量与原向量的方向是否相同。
- $k$ 为 $0$ 时,会得到一个零向量。
向量数乘的代数意义
对于: $$ \vec{a} = \begin{pmatrix} a_{1}\\ a_{2}\\ a_{3} \\ \ldots \\ a_{n} \end{pmatrix} $$, 数乘的代数意义可表达为其每个分量与系数 $k$ 相乘再组成的新向量,即: $$ k\vec{a} = k\begin{pmatrix} a_{1}\\ a_{2}\\ a_{3} \\ \ldots \\ a_{n} \end{pmatrix}= \begin{pmatrix} ka_{1}\\ ka_{2}\\ ka_{3} \\ \ldots \\ ka_{n} \end{pmatrix}, k \in \mathbb{R} $$
相关性质
向量的加法满足交换律与结合律,即:
- $\vec{a}+\vec{b} = \vec{b} + \vec{a}$
- $\vec{a} + \vec{b} + \vec{c} = \vec{a} + (\vec{b}+\vec{c})$
向量的数乘满足交换律,结合律,分配律,即:
- $\vec{a} \cdot k = k \cdot \vec{a}$
- $\vec{a} \cdot m \cdot k = k \cdot (m \cdot \vec{a})$
- $k \cdot (\vec{a} + \vec{b})= k \cdot \vec{a}+ k \cdot\vec{b}$
线性表示与线性相关
在讨论线性相关的概念之前,先来看下面的例子:
我们的人眼大概有三种感光细胞。这三种细胞分别能分辨出红色、绿色、蓝色。不过实际上,我们看到的世界是五彩缤纷的;也就是说,通过这三种感光细胞的混合使用,我们能够分辨非常多的颜色。但实际上,这些我们看到的颜色,实际上都是由红绿蓝三种颜色组成的。因此我们将红绿蓝三种颜色称为三原色,简称为 $RGB$:
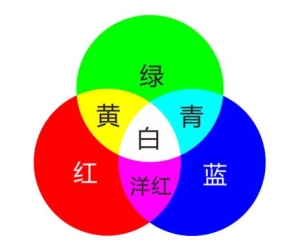
下面则是一些通过三原色组合得到的新颜色:
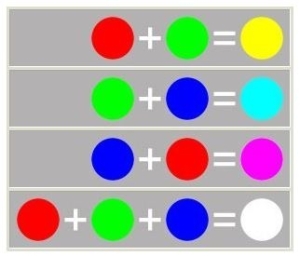
下面我们来对上面这些信息进行数学化。假设 $RGB$ 各为一个长度为 $3$ 的向量,其每个分量的上限是 $255$,那么我们的红绿蓝三原色则可以表示为:
$$
R: \begin{pmatrix}
255\\
0\\
0
\end{pmatrix}\,\,\,\,
G: \begin{pmatrix}
0\\
255\\
0
\end{pmatrix}\,\,\,\,
B: \begin{pmatrix}
0\\
0\\
255
\end{pmatrix}
$$
假设有一种海棠色,分别需要强度为 $255$ 的红色光线、$52$ 的绿色光线、$85$ 的蓝色光线混合组成,那么实际上我们可以将海棠色表示为代表红绿蓝的三个向量的运算:
$$
\begin{pmatrix}
255\\
52\\
85
\end{pmatrix} \approx
\begin{pmatrix}
255\\
0\\
0
\end{pmatrix} +
\frac{1}{5}\begin{pmatrix}
0\\
255\\
0
\end{pmatrix} +
\frac{1}{3}\begin{pmatrix}
0\\
0\\
255
\end{pmatrix}$$
我们发现,某些向量可以通过一些基础的向量进行运算而得到。也就是说,这个向量可以表示用某一组基础向量来表示。我们将这样的一组向量(集合),称为向量组。下面是向量组的定义:
若干同维数的列向量(或者同维数的行向量)所组成的集合,叫做向量组。
显然,先前例子中的 ${R,G,B}$ 就是一个向量组。
因为海棠色可以由三原色组成,因此我们称代表海棠色的向量可以由代表三原色的向量线性表示;换句话说,代表海棠色的向量是向量组 ${R,G,B}$ 的一个线性组合。来看下正式的定义:
给定向量组 $A:\vec{a_1},\vec{a_2},...\vec{a_m}$ 和向量 $\vec{b_{}}$,如果存在一组实数 $k_1,k_2,...,k_m,$ 使:
$$\vec{b_{}}=k_1\vec{a_1}+k_2\vec{a_2}+...+k_m \vec{a_m}$$则称向量 $\vec{b_{}}$ 能由向量组 $A$ 线性表示,也可以说向量 $\vec{b_{}}$ 是向量组 $A$ 的线性组合。
线性相关
通过上面的例子,我们发现海棠色可以由三原色“调”出来。但同时,我们也发现,三原色之间是无法互相“调”出来的:我们没有办法用红色表示绿色,或者蓝色。
在数学中,如果一个向量能被另外一组向量表示出来,那么我们就说该向量与对应的向量组线性相关。反之,我们就说该向量与对应的向量组线性无关。比如这里的海棠色,与 向量组 ${R,G,B} $ 线性相关;而 $R$ 则与 向量组 ${G,B}$ 线性无关。
从以上的信息我们也可以推导出:如果一个向量能被某一个向量组线性表示,那么这个向量与可以线性表示它的向量组组成的新向量组,也是线性相关的。
这里马同学讲的并不是很清楚。我姑且理解为判断一个向量是否与一个向量组线性相关的条件是该向量能被向量组线性表示;而判断一个向量组是否线性相关(注意这里是单个的向量组)的条件则是,该向量组内的任意向量可以被同组的另外多个向量组成的向量组线性表示。
来看下线性相关正式的定义:
给定向量组 $A:\vec{a_1},\vec{a_2},...\vec{a_m}$,如果存在不全为零的实数 $k_1,k_2,...,k_m$,使
$$k_1\vec{a_1}+k_2\vec{a_2}+...+k_m\vec{a_m}=\vec{0},$$ 则称向量组 $A$ 是线性相关的,否则称它为线性无关。
注意这里线性无关的条件是 实数 $k_1,k_2,...,k_m$ 全部为零。
上面这个等式很好理解。如果我们将左边的其中一项移到右边,当等式成立,也就是向量组线性相关的时候,我们发现右边的向量可以由左边的某些或全部向量组线性表示。
常见的线性相关判断
线性相关的判断有一些常见的定理:
- 单元素的向量组:仅含一个向量 $\vec{v}$ 的向量组线性无关,当且仅当 $\vec{v}$ 不是零向量。
- 两个元素的向量组:两个向量的集合 $\{\vec{v_1},\vec{v_2}\}$ 线性相关,当且仅当其中一个向量是另一个向量的倍数(也就是几何中的共线)。
- 多个向量的向量组:这种情况需要进行具体的判断。
- 含零向量的向量组:若向量组 $S=\{\vec{v_1},...,\vec{v_n}\}$ 包含零向量,则该向量组线性相关(零向量与向量组的任意向量共线)
向量空间
之前我们提到,向量可以由坐标系的点表示,而且向量与坐标系里的每个点都是一一对应的。那么,我们应该怎么描述所有向量(所有点)形成的概念?
可以来看看由向量组成的概念具有那些性质:
- 具有元素(该概念由向量组成,因此元素是向量)
- 具有运动(可以在其中进行向量的操作)
- 封闭性(经过向量的操作,生成的新向量依然属于概念中)
我们将这样的概念称为向量空间。
再从数学上来看看这三个性质怎么描述。如果将向量空间表示为 $V$:
首先,向量空间具有元素向量,因此向量空间可以表示为:
$$V=\{\vec{v_1},\vec{v_2},\cdots,\vec{v_n}\}$$
其次,向量空间具有运动。根据我们已知的向量的操作,数学上可以将其描述为加法与数乘,即:
- $\vec{v_1}+\vec{v_2}$ 生成新的向量
- $k\vec{v_1},k\in\mathbb{R}$ 缩放向量
再次,生成的新向量依然在空间中。也就是说,需要满足以下关系:
- $\vec{v_1}+\vec{v_2} \in V$
- $k\vec{v_1},k\in\mathbb{R} \in V$
通过以上,我们可以得到向量空间正式的数学定义:
设 $V$ 为一向量组。
如果 $V$ 非空,且 $V$ 对于于向量的加法及数乘两种运算封闭,那么就称 $V$ 为向量空间。
所谓封闭,是指在V中向量进行数乘和加减,其结果依然在 $V$ 中(即向量空间性质第三条)。
向量空间的例子
二维空间
显然二维空间满足向量空间的所有要求:
- 包含向量(二维空间所有点可以用向量表示)
- 包含向量的运动(二维空间内可以对向量进行平移和拉伸)
- 封闭性(新生成的向量也在二维空间内)
色彩空间
$RGB$ 色彩空间同样满足要求:
- 包含向量(红绿蓝可以视作向量)
- 包含向量的运动(颜色可以叠加,缩放)
- 生成的新颜色仍然属于 $RGB$ 色彩空间。
多项式
如果以 $\{1,x,x^2,\cdots,x^n\}$ 为基,则多项式 $a_0+a_1x+a_2x^2+\cdots+a_nx^n$ 可以如下的向量形式: $$ \begin{pmatrix}
a_{0}\\
a_{1}\\
a_{2} \\
...\\
a_{n}
\end{pmatrix} $$
显而易见的是,任意一个符合写法的多项式,都可以表示为向量。
除此之外,我们注意到多项式也可以进行加法与数乘的操作,而这些操作与向量的操作是等同的,比如:
$$
(a_0+a_1x+a_2x^2+\cdots+a_nx^n)+(b_0+b_1x+b_2x^2+\cdots+b_nx^n) = \begin{pmatrix}
a_{0}\\
a_{1}\\
a_{2} \\
...\\
a_{n}
\end{pmatrix} +
\begin{pmatrix}
b_{0}\\
b_{1}\\
b_{2} \\
...\\
b_{n}
\end{pmatrix}
$$
而这样得到的结果,显然也是可以用该多项式表示的:
$$\begin{pmatrix}
a_{0}\\
a_{1}\\
a_{2} \\
...\\
a_{n}
\end{pmatrix} +
\begin{pmatrix}
b_{0}\\
b_{1}\\
b_{2} \\
...\\
b_{n}
\end{pmatrix} =
\begin{pmatrix}
a_{0} + b_{0}\\
a_{1} + b_{1}\\
a_{2} + b_{2}\\
...\\
a_{n} + b_{n}
\end{pmatrix}$$
即:
$$(a_0+b_0)+(a_1+b_1)x+(a_2+b_2)x^2+\cdots+(a_n+b_n)x^n$$
因此,多项式也是向量空间。
注意:不含有零向量的向量组一定不是向量空间。这个是很好证明的:如果向量空间中所有向量进行 $0$ 的数乘,那么得到必然是一个零向量。如果向量空间不包含零向量,那么得到的新向量(零向量)就破坏了向量空间的第三个性质:封闭性。
子空间
由 $n$ 维向量组成的向量空间的维数通常与其向量相等,记做 $\mathbb{R^n}$ 。但有时候,有时候向量空间的维数是要低于组成其向量的维数的。来看看下面的例子:
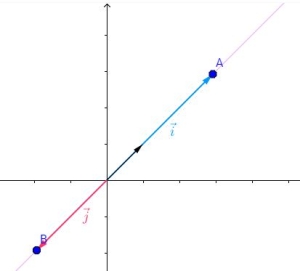
如图,$\vec{i}$ 与 $\vec{j}$ 均属于 $\mathbb {R^2}$,但他们组成的向量空间是一条直线。而显然,该直线是 $\mathbb {R^2}$ 的子空间。
注意:子空间也是向量空间,因此也必须包含零向量。
如何判断是否是子空间
是否是子空间可以通过定理来判断:
- 判断子空间是否具有零向量
- 判断子空间是否加法封闭
- 判断子空间是否乘法封闭
- 某些简单例子可以通过几何方法来判断
基
张成空间
回忆一下之前的 $RGB$ 组成的向量空间,我们发现这个向量空间既包含三原色代表的向量,也包含由三原色组合形成的颜色向量(线性组合)。对于这样的情况数学上称,$RGB$ 空间由代表红绿蓝的向量张成;而由这些向量与向量的线性组合组成的空间,我们称之为该 $RGB$ 的张成空间。来看一下正式的定义:
向量空间 $V$ 中一向量组 $\vec{v_1},\vec{v_2},...,\vec{v_p}$,其所有线性组合构成的集合称为 $\vec{v_1},\vec{v_2},...,\vec{v_p}$ 的张成空间,记为 $span(\vec{v_1},\vec{v_2},...,\vec{v_p})$,即:
$$span(\vec{v_1},\vec{v_2},...,\vec{v_p})=\{c_1\vec{v_1}+c_2\vec{v_2}+...+c_p\vec{v_p},c_1,c_2,...,c_p\in\mathbb{R}\}$$我们也称 $span(\vec{v_1},\vec{v_2},...,\vec{v_p})$ 为 $\vec{v_1},\vec{v_2},...,\vec{v_p}$ 所张成。
等价向量组
代表红绿蓝的向量可以对 $RGB$ 色彩空间进行描述。不过人们发现,我们不仅可以用红绿蓝来描述色彩,也可以用 $CMY$ (青色、洋红、黄色)来描述色彩:

不但如此,通过上图我们发现,这两组向量居然是可以互相表示的。也就是说,这两个向量组可以相互线性表示。我们将这样的两个向量组称为等价向量组。下面是正式的定义:
设有两个向量组 $A:\vec{a_1},\vec{a_2},...,\vec{a_m} $及$ \vec{b_1},\vec{b_2},...\vec{b_l}$,若 $B$ 组中的每个向量都能由向量组 $A$ 线性表示,则称向量组 $B$ 能由向量组 $A$ 线性表示。若向量组 $A$ 与向量组 $B$ 能相互线性表示,则称这两个向量组等价。
等价向量组与向量空间
我们知道,$RGB$ 与 $CMY$ 表示的是同一个色彩空间。由此我们可以想到:等价的向量组所张成的向量空间应该相等,即:
$$
\begin{align}
A=\{a_1,a_2,...,a_n\}\quad&\sim\quad B =\{b_1,b_2,...,b_m\} \\\\
&\Downarrow \\\\
span(A)\quad&=\quad span(B)
\end{align}
$$
一个具体的例子就是,假设我们有向量组 $A=\{\vec{i}=(1,0),\vec{j}=(0,1)\}$,向量组 $B=\{\vec{i'}=(1,1),\vec{j'}=(-1,1)\}$。两个向量组等价,而他们以不同的方式张成了等价的向量空间 $\mathbb {R^2}$:
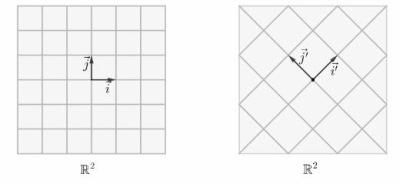
最大无关线性组
我们知道 $RGB$ 色彩空间中,红绿蓝是不能相互线性表示的。假设红绿蓝组成的向量组为 $A_{0}$, 现在我们再往中加入黄色,组成一个新的向量组 $A$:${R,G,B,Y}$。
我们知道黄色可以由红色与绿色生成。根据线性相关的定义,我们可得知 $A$ 这个向量组是线性相关的,而 $A_{0}$ 是线性无关的。
这种情况下,我们称向量组 $A_{0}$ 为 $A$ 的一个最大线性无关向量组。正式的定义如下:
设有向量组 $A$,如果在 $A$ 中能选出 $r$ 个向量 $\vec{a_1},\vec{a_2},...,\vec{a_r}$ 满足:
* 向量组 $A_0:\vec{a_1},\vec{a_2},...,\vec{a_r}$ 线性无关
* 向量组 $A$ 中任意 $r+1$ 个向量(如果 $A$ 中有 $r+1$ 个向量的话)都线性相关
那么称向量组 $A_0$ 是向量组 $A$ 的一个最大线性无关组(简称最大无关组)。最大无关组所含向量个数 $r$ 称为向量组 $A$ 的秩,记做 $rank(A)$ ,有时也记作 $R(A)$。只含零向量的向量组没有最大无关组,而我们规定它的秩为$0$。
基的基本概念
再回到 $RGB$ 这个例子。根据最大无关线性组的定义,红绿蓝可以作为色彩空间的一个最大无关组(所有其他颜色都可以通过红绿蓝线性表示)。我们把这样一组向量,称为色彩空间的一个基。以 $RGB$ 三色为基的色彩空间,被称为 RGB 色彩空间。
来看看基的正式定义:
设 $V$ 为向量空间,如果 $r$ 个向量 $\vec{a_1},\vec{a_2},...\vec{a_r}\in V$,且满足 $\vec{a_1},\vec{a_2},...,\vec{a_r} $线性无关、$V$ 中任意向量都可由 $\vec{a_1},\vec{a_2},...,\vec{a_r}$ 线性表示;
那么,向量组 $\vec{a_1},\vec{a_2},...,\vec{a_r}$ 被称为向量空间 $V$ 的一个基。
两个同维数的向量组,若其中一个线性无关,那么另外一个也线性无关的充要条件是两个向量组的秩相等。
基的不唯一
由 $RGB$ 与 $CMY$ 的例子我们可以看出,$RGB$ 与 $CMY$ 可以张成相同的色彩空间。又因为这两个向量组均是色彩空间的最大无关线性组,因此,这两个向量组都可以被称为色彩空间的基。由此可见,一般情况下,对于向量空间,基并不是唯一的。
自然基
基是向量空间的最大无关线性组,那么也就意味着向量空间里所有的向量都可以用基表示。换句话说,向量空间中所有的坐标(点)都可以用即表示。然而我们之前已经知道,对于同一个向量空间来说,基是不唯一的。因此,使用不同的基来表示的向量,结果会造成坐标系衡量标准不同。也就是说,选择了不同的基,就选择了不同的坐标系。
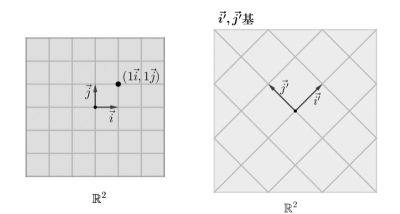
因此,坐标的定义则可以表述为:
如果在向量空间 $V$ 中取定一个基 $\vec{a_1},\vec{a_2},...,\vec{a_r}$ ,那么 $V$ 中任一向量 $\vec{x}$ 可唯一的表示为:
$$\vec{x}=k_1\vec{a_1}+k_2\vec{a_2}_+...+k_r\vec{a_r}$$数组 $k_1,k_2,...,k_r$ 称为向量空间 $\vec{x}$ 在基 $\vec{a_1},\vec{a_2},...,\vec{a_r}$ 中的坐标。
(这个很好理解:每一个分量对应的系数组合起来,就是该向量在当前坐标系的坐标。)
基是不唯一的,为此我们需要找出一个基作为标准化的参照;于是有了自然基。自然基的定义如下:
在 $n$ 维向量空间 $\mathbb{R^n}$ 中取单位坐标向量组 $\vec{e_1},\vec{e_2},...,\vec{e_n}$ 为基,则 $x_1,x_2,...,x_n$ 为分量的向量 $\vec{x}$ ,可表示为:
$$ \vec{x}=x_1\vec{e_1}+x_2\vec{e_2}+...+x_n\vec{e_n}$$可见,向量在基 $\vec{e_1},\vec{e_2},...,\vec{e_n}$ 中的坐标就是该向量的分量。因此, $\vec{e_1},\vec{e_2},...,\vec{e_n}$ 叫做 $\mathbb{R^n}$ 中的自然基。
乍看这个定理,说的确实比较抽象。参考WIkipedia 的解释之后,从几何的角度可能更好理解自然基这个概念。以三维空间为例,它的自然基就是与三个坐标轴方向分别相同的三个向量组成的向量组: $ {(1,0,0), (0,1,0),(0,0,1)}$。
很明显的是,自然基的成员向量具有两个特点:
- 在与对应坐标轴相同的方向上的长度为 $1$(也就是单位向量)
- 除此之外其他方向的分量均为 $0$
即使 $n\geq4$ 后没有几何解释,我们也可以很容易的将这种解释推广到 $n$ 维向量空间中。
维度与秩
基作为向量空间的最大无关线性组也是拥有秩的。但与将一般的最大无关线性组称为秩不同,通常我们将基的秩(也就是向量空间的秩)称为维度。比如 $\mathbb {R^2}$ 的秩为 $2$:
$$\mathbb {R^2} = {(x,y)|x,y \in \mathbb {R}} \xrightarrow{basis} \underbrace{ {(1,0), (0,1)} }_\text {2}$$
我们可以简单概括一下:
若向量组 $\vec{a_1},\vec{a_2},...,\vec{a_r}$ 是向量空间的一个基,则向量组的秩 $r$ 就称为向量空间的维数,并称向量空间为 $r$ 维向量空间。如果向量空间没有基,那么它的维数为$0$,$0$维向量空间只含一个零向量。
向量的维度与空间的维度
向量的维度在某些情况下与向量空间的维度不相等。以三维空间为例,我们很多时候认为三维向量只能存在于三维空间中,其实不然。某些向量不但能存在三维空间中,而且能存在于三维空间的子空间中,比如一个平面,甚至一条直线。不过需要注意的是,三维向量是不能存在于四维空间中的,也就是说:
$$向量的维数 \geq 空间的维度$$
点积
向量空间具有描述现实空间的基础;为了更好的描述现实空间,古希腊数学家提出了一种用于描述现实的世界空间,数学上称为欧几里得空间。和我们的向量空间相比,这种空间多了两个概念:长度与角度。
而为了从数学上描述长度与角度,欧几里得空间在向量空间的基础上添加了一个运算点积。我们来看看点积这个运算是怎么描述角度与长度的。
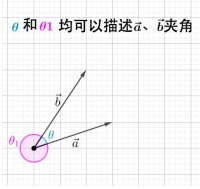
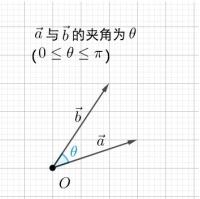
角度
角度的计算
有了角度的定义,再来看看角度是怎么计算的:
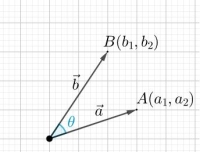
如上图所示,根据欧式几何中的余弦定理,可得:
$$AB^2=OA^2+OB^2-2OA\cdot OBcos\theta$$
将上述的线段表示转化为向量,则有:
$$||\vec{a_{}}-\vec{b_{}}||^2=||\vec{a_{}}||^2+||\vec{b_{}}||^2-2||\vec{a_{}}||||\vec{b_{}}||cos\theta$$
对上面的式子进行化简,有:
$$
\begin{aligned}
||\overrightarrow{a_{}}-\overrightarrow{b_{}}||^2
&=(a_1-b_1)^2+(a_2-b_2)^2\\
\quad\\
&=\underbrace{(a_1^2+a_2^2)}_{||\overrightarrow{a}||^2}+\underbrace{(b_1^2+b_2^2)}_{||\overrightarrow{b}||^2}-2a_1b_1-2a_2b2\\
\quad\\
&=||\vec{a_{}}||^2+||\vec{b_{}}||^2-2||\vec{a_{}}||||\vec{b_{}}||cos\theta
\end{aligned}
$$
整理一下可得:
$$cos\theta=\displaystyle\frac{a_1b_1+a_2b_2}{||\vec{a_{}}||||\vec{b_{}}||}$$
到此我们得到了 $cos\theta$,通过求其反函数,就可以得到夹角的大小了。
现在我们希望用向量来表示整个表达式,因此我们用点乘符号 来表示 $a_1b_1+a_2b_2$, 即:
$$\vec{a}\cdot\vec{b}=a_1b_1+a_2b_2$$
这个过程,我们就称为向量的点积。而前面提到的计算夹角的公式,就可以变为:
$$cos\theta=\displaystyle\frac{\vec{a}\cdot\vec{b}}{||\vec{a}||||\vec{b}||}$$
长度
根据勾股定理,某一条向量的长度可以由另外两边求出,即:
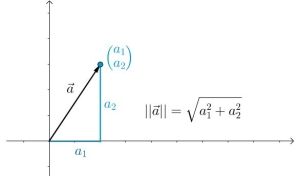
用之前我们提到的点积来表示这个过程。将 ${a_1}^2$ 与 ${a_2}^2$ 的和视作 $\vec a$ 自身的点积,那么有:
$$\vec{a}\cdot\vec{a}=a_1 \cdot a_1 +a_2 \cdot a_2=||\vec{a}||^2$$
即:
$$||\vec{a}||=\sqrt{\vec{a}\cdot\vec{a}}$$
点积
我们之前在 $\mathbb {R^2}$ 中用点积表示了长度与角度;将其推广到 $\mathbb{R^n}$,就可以得到以下点积的正式数学定义:
在向量空间 $\mathbb{R}^n$ 中,向量 $\vec{x}=(x_1,\ldots,x_n)$ 和 $\vec{y}=(y_1,\ldots,y_n)$ 的点积 (dot product),或称内积 (inner product),定义为:
$$\vec{x}\cdot\vec{y}=x_1y_1+\cdots+x_ny_n=\displaystyle\sum_{i=1}^{n}x_iy_i$$
点积的性质
点积具有以下的三种性质:
- 交换律:$\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a}$
- 数乘结合律:$(k\vec{a})\cdot\vec{b}=k(\vec{b}\cdot\vec{a})$
- 分配律:$(\vec{a}+\vec{b})\cdot\vec{c}=\vec{a}\cdot\vec{c}+\vec{b}\cdot\vec{c}$
根据之前的角度公式,我们可以得到:
$$\vec{a}\cdot\vec{b}=||\vec{a}||||\vec{b}||cos\theta$$
从几何上来说,$\vec{a}\cdot\vec{b}$ 的几何意义就是一条乘以另外一条在其上的投影:
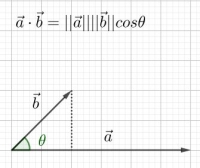
关于这个几何意义是如何得来的,请参考这里:(需要学习完矩阵变换的知识)。
再来看看对于点积的性质的几何解释。根据之前的说明,点积可以看做是两条向量长度的乘积;因此点积的结果可以看作是一个如下的矩形:
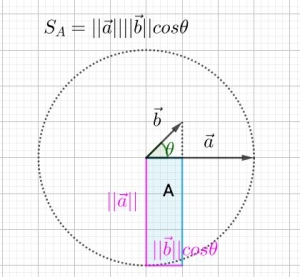
那么这样一来,从集合上解释点积的几个性质就很容易了:
首先,因为向量的点乘可以表述为两个长度的乘积,所以交换律是肯定适用的。
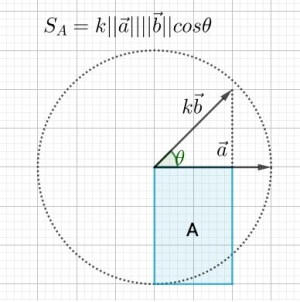
其次,如果我们将一条向量的长度放大 $k$ 倍,那么得到的面积也必然放大 $n$ 倍,因此数乘的结合律也是成立的:
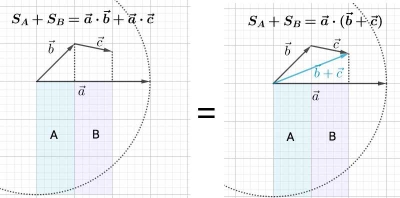
再来看分配律。我们发现,两个向量分别与第三个向量进行点积运算后得到的面积大小,实际上与他们之和与第三个向量进行点积运算后得到的大小是一样的,原因是因为前两个向量在第三个向量上的投影长度之和等于其和的投影长度:
点积的应用
点积的第一个作用是用来求距离。点积可以分别描述长度与角度,因此我们将点积所求的距离分为欧氏距离(长度)和余弦距离(角度)。
欧式距离是指两个向量之间的距离。根据三角形法则,其长度可表示为:
$$|AB|=||\vec{a}-\vec{b}||$$
再根据点积的长度公式,其长度可以表示为:
$$||\vec{a}-\vec{b}||=\sqrt{(\vec{a}-\vec{b})\cdot(\vec{a}-\vec{b})}$$
而余弦距离,也就是我们所说的余弦值。根据点积的角度公式,我们可以发现:
- 当两个向量方向相近的时候,余弦值为正
- 当两个向量垂直的时候,余弦值为零(我们称这种情况为向量的正交)
- 当两个向量方向相腻的时候,余弦值为负
鉴于向量的夹角取值范围为 $[0, \pi]$,我们发现在两个向量在方向相同的时候,余弦值达到最大值 $1$,而完全相反的时候,余弦值达到 $-1$。
可以看出来的是,余弦距离可以很好的描述两个向量之间的方向关系。而当向量空间超出三维以后,余弦距离可以用于解释向量所代表数据之间的相关性,如下图:
<html>
<img src=“/_media/math/linear_algebra/ma/cosdistance.svg” width=“500”>
</html>
也就是说:
- 余弦值的绝对值代表了两组数据的相关性,绝对值也大,相关性越强(可能是爱也可能是恨
)
- 两组数据完全不相关的时候,也就是代表他们的向量处于正交状态的时候
查漏补缺
向量组是否能互相表示
可以通过向量组的秩来判断:秩相同,且其中一个能线性表示另外一个,那么两个向量组可以互相表示。
线性无关与维度
- 线性无关的向量,升维度后依然线性无关
- 线性相关的向量,降维度后依然线性相关