S.B.S book Chapter 3 notes

为什么要引进 集中趋势 （Central Tendency）这一概念?

很多情况下，我们通过频数分布表推断的出的结果并不像我们想象中的那么准确。比如如果两个组的分布重合较多，我们就很难通过直接对比分布图来得出正确的结果。

为了解决这个问题，统计学中提出了一个新的概念：集中趋势。这个概念是一种应用于整个分布的测量标准；一般说来，这个概念定义了整个分布的中心点。而我们希望用这个概念来找出一个最有代表性的数据来表示整个组。

Central tendency is a statistical measure to determine a single score that defines the center of a distribution. The goal of central tendency is to find the single score that is most typical or most representative of the entire group.

在很多情况下，集中趋势这个概念可以与 “平均值”（Avenge）等同；比如天气预报中的平均温度，平均降雨量等等，这些数据都可以在某种程度上直接反应某些年的天气趋势。换句话说，通过该平均值，天气的变化更容易描述了。

不过遗憾的是，平均值并不能准确的描述某些场景。来看看下面的例子：



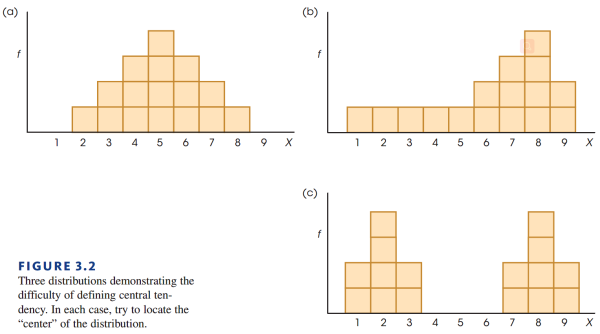
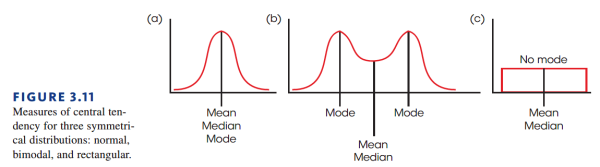
来分别看看对于上面的例子：

• 例 a，对称分布，因此中心处 $X=5$ 可以很好的表示整个组。
• 例 b, 这个分布范围在1-9之间，但是很显然呈现负偏态分布。它的中心点是多少？看起来 $X=8$ 的频数最高，但是平均起来大多数分数都小于 8。因此我们并没有一种无争议的方法确定其中心。
• 例 c，这个分布虽然是对称的，但是分数集中在两边。它的中点是 $X=5$ ，但是却没有任何一个分数是5。$X=2$ 和 $X=8$ 是两群集中的分数的中心，但是一个分布可以有两个中心吗？

因此可以看出，我们并没有一种标准、无争议的方法确定集中趋势。针对上述的这些常见的分布，我们将集中趋势大致分为三种：平均值（Mean）、中位数（Median）、众数（Mode）。

平均值，又被称为算术平均数（Arithmetic average），其计算方法就是用分布中所有分数的和除以个体的总个数。

The mean for a distribution is the sum of the scores divided by the number of scores.

针对总体和个体，平均值的记号不同：

• 针对总体的记号是 $\mu$，读作“谬”
• 针对样本的记号分两种：
  • 如果用于研究报告，使用 $M$ 作为样本的平均值记号
  • 一般的书中记做 $\bar{X}$，读作 “x-bar”

使用上述记号，平均值的公式可以表示如下： $$ \mu = \frac{\sum X}{N} \\ M = \frac{\sum X}{n} $$

• Dividing the Total Equally ：平均数可以想象成组中每个个体平均分配总的分数
• Balance Point：将频数分布图想象成一个跷跷板，平均数就是跷跷板的平衡点。

有时候我们需要计算好几个组的平均值。比如我们知道两个班分别的平均分和班级人数，要想计算两班总体的平均分，那么计算方法应该如下：

$$ M = \frac{\sum X_1 + \sum X_2}{n_1 + n_2} $$

比如，一班平均分80分、共有60人，二班平均分90分、共有40人。两个班整体的平均分为：
$$M=\frac{80\times 60+90\times 40}{60+40}=\frac{8400}{100}=84$$
也就是第一班的总分数加上第二班的总分数，除以两个班的总人数。而需要注意的是，两个班的人数可能不同，总分数可能不同。换句话说，将两个班放在一起的时候，每个班对于总体的“贡献”可能也不同，因此我们不能简单的将两个班的平均成绩加起来除以二来得到两个半总体的平均分数。因为这个原因，我们又将这种平均数称为加权平均数（Weighted mean）。

我们也可以从“贡献”的角度来考虑：一班有全体人数的 $60%$ 的人数，它对整体平均分的贡献应当就是 $60%$ ，同理二班就是 $40%$。把这个“贡献程度”分别乘以各班平均分，也能得到相同的结果：
$$M=80\times 60\%+90\times 40\%=48+36=84$$

需要注意的是，每个分数都对平均分的计算有贡献，因为每一个分数既参与了总分数的累积，也参与了个体数量的累积。因此如果改变其中一个分数，那么平均数一定会变，因为总分数会变，但个体数量没有发生变化。

如果增加或去掉一个个体，除非这个个体的分数恰好等于平均数，否则平均数也一定会变。一种直观的理解方式如下：

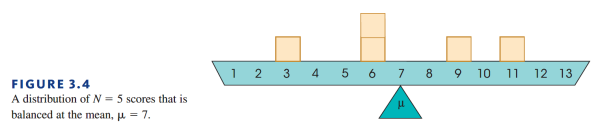
如果把整个分布当成一个天平，那么在平衡状态时支点一定就是平均数那一点。如果增加或去掉一个分数，那么除非这个分数就在支点的正上方，否则天平一定会倾斜，必须调整支点的位置才能重新平衡。

同时需要注意，添加或者去除个体（分数）对总体和样本同样有影响。

如果将每一个分数都加、减、乘或者除以一个固定的常数（除数不为 0），那么平均数也应当相应加、减、乘或者除以这个常数。乘除操作常用于对目标组的计量单位的换算，比如长度之间的换算。

集中趋势的第二种测量尺度称为中位数（Median）。中位数 的目标是找出整个分布的中间点（Midpoint）。因为对于每种分布，中间点都有不一样的描述，因此我们没有办法用统一的符号来描述中位数。取而代之的是，我们用词：中位数 来描述这个概念。

If the scores in a distribution are listed in order from smallest to largest, the median is the midpoint of the list. More specifically, the median is the point on the measurement scale below which 50% of the scores in the distribution are located.

找出中位数有两个前提：

• 必须对整个分数组进行从小到大的排列。
• 中位数必须处于分布的中间点，也就是可以将整个分布分成两个相同大小组的点。

对于离散变量来说，中位数分为以下的两种情况：

• 如果分数的个数为奇数，那么最中间的一位分数就是中位数。
• 如果分数的个数是偶数，那么最中间的两个分数的平均数就是中位数。

比如下面的例子：

$$3,5,8,10,11$$
最中间的是 8，所以中位数是 8。再比如：
$$1,1,4,5,7,8$$
最中间的两个是 4 和 5，取它们的平均数，中位数就是 4.5。

连续变量的中位数计算与离散变量类似；不同之处在于，连续变量表示的是区间。因此，我们可以精确的找出指定分布的中间点，并将其作为该分布的中位数。

来看一个例子。比如我们有一个包含 $8$ 个分数的样本如下：
$$1,2,3,4,4,4,4,6$$
如果该组变量是离散变量，那么很明显，该组变量的中间数是 4。可是如果是连续变量呢？

来看一下下面的分布图：



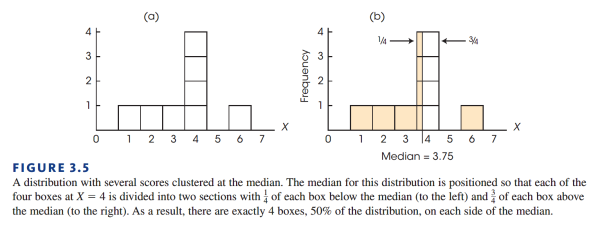
我们知道，离散变量中的 4，在连续变量中其实表示为区间 3.5-4.5。但是，中间数永远都一个点，因此上图中作为离散变量分布中的中间数 4，就不能再作为连续变量的中间数了。下面是求上图连续变量的中间数的大概步骤：

1. 我们观察到整个分布由 8 个分数表示的区间组成，每一个分数占了一个格子。
2. 按照中位数的定义，中位数必须能将该区域平均分成两部分。
3. 第一部分应该由 $1,2,3$ 和四个 4 中的，靠近左边的 4 组成，也就是 ${1,2,3,4}$
4. 第二部分应该由四个 4 中的其余三个 4，与剩下的 6 组成，也就是 ${4,4,4,6}$
5. 在分布图中，4 对应的区块有 4 个，都处于中间。但因为第一部分只有一个 4，第二部分有三个 4，为了保证中位数恰好位于整个分布的中心，那么 4 这个分数需要按前后部分所占 4 的比例来划分。本例中是 $1：3$，因为整个区间的宽度是 1，因此中位数的位置是：

$$3.5+1\times \frac{1}{4}=3.75 $$

同时，按照百分位数的定义，中位数也可以表示为 50th Percentile。因此对于上例，我们也可以按照百分位数的定义来计算中位数。本例中个体总数为 8, 3.5 处的累积频率为 $3 / 8 = 37.5%$，4.5 处的累积频率为 $7 / 8 = 87.5%$。根据百分位数的定义：

$$ cf(50) = 3.5+1\times \frac{50\%-37.5\%}{87.5\%-37.5\%}=3.5+\frac{12.5\%}{50\%}=3.5+0.25=3.75 $$

除了平均数与中位数，我们还有一种测量标准来衡量集中趋势，也就是众数（Mode）。众数代表了频数出现最多的分数（类别）。

In a frequency distribution, the mode is the score or category that has the greatest frequency.

相较于平均数与中位数，众数的适用性更广。比如下面的例子，我们需要处理一个类别量表：



这个表中我们需要测量学生们最爱去的餐馆。因为是类别量表，因此平均数和中位数都不能被用于该测量。而上图中的众数，Luigi's，就能完美的表现出测量的结果。

另外需要注意的是，一个分布中可以拥有不止一个的众数。在分布中，如果有多个分数或类别对应的频率并列最高，那么这些分数和类别都是众数。我们将这样的分布大致分为两类：

• 双峰分布（Bimodal distribution）：有两个众数的分布
• 多峰分布（Multimodal distribution）：有两个以上众数的分布

如何针对不同的分布采用不同的集中趋势来测量呢？

首先要明确的是，如果分数是以数值的形式存在，一般来说使用平均数作为集中趋势是最合适的。因为平均数来源于分布中的所有分数，因此其本身就是一个可以很好表达整个分布的值。除此之外，平均数对方差与标准差的生成起到了不可或缺的作用。因此，平均数本身可以认为是三种集中趋势中最好的一种。

不过在很多特定的情况下，我们也需要采用中间数、众数来解决实际问题。

总的来说，在数据由数值组成的前提下，有三种情况我们可以使用中位数来取代平均数：

1. 无法计算平均数
2. 平均数的值不处于分布的中心
3. 平均数的值无法代表整个分布

还有一种情况是我们需要测量顺序量表的集中趋势，那么这种情况是无法使用平均数计算的。

如果分布中存在少数与分布中其他分数差异十分巨大的分数，那么这些分数将会对平均数造成非常大影响。比如，有 10 个人参加考试，9 个人的分数都是在 90 分以上，只有一个人分数只有 5 分，那么如果简单地把 10 个人的分数作平均，得到的结果并不能体现这 10 个人整体的分布情况，因为平均分会被那个 5分的人显著拉低。

而从另外一方面看，中位数基本上不会被被比较极端的分数影响。在排序后的分数序列中，中位数的位置永远是在 50% 的位置的，而极端的分数一般都在分布的最左或者最右。由于这种特性，中位数一般用于表示偏态分布的平均值。

某些情况下，个体会带有一些位置的分数。这种情况主要出现在有前提的测量中，比如测量完成任务所消耗的时间。在这种类型的测量中，我们会遭遇到一种很尴尬的情况：任务无法完成，无法测量消耗的时间。比如如下的频数分布表：



注意到上图有个人无法完成任务。我们应该怎么处理这个数据呢？

首先，这个数据是不能被丢弃的。我们的目标是对整个总体进行测量，而这个人的数据告诉了我们总体中存在有人不能完成任务的情况。其次，即便该个体没有完成任务，我们也不能使用任务完成时间来取代不能完成任务作为分数值，因为我们并不知道该个体完成任务需要多少时间。

因此，平均数是无法处理这种情况的，因为存在未知的分数，所以我们无法求得平均数。但我们可以通过中位数来表达整个分布。这种情况下，中位数的可计算性是显而易见的。

有一种分布被称为开口分布（Open-ended distribution）。这种分布有一个显著的特点：在这个分布中，有某个类别没有上界和下界。来看下面的一个关于学生消费披萨的例子：



注意看数据的第一行：5 or more。这就是一个很典型的没有上限的类别，因为我们并不知道该类别中的学生具体吃掉了多少个披萨。同样，对于这种情况，我们也无法计算平均数，也需要使用中位数来表示整个分布。

如果一个量表有确定的顺序，但是并不能量化地体现它们的准确关系，那么同样没办法计算其平均值。因为其本身的“距离”并没有被量化。就好像去星巴克点咖啡，店员问你要什么尺寸，你可以点大杯、中杯、小杯。杯子的尺寸是可以排序的，但是不能被准确度量的；我们并不能说中杯是小杯和大杯的平均值。因此这种情况下，我们只能选择中位数。

通常有三种情况需要使用众数。

众数最大的优势就是其可以描述类别量表的集中趋势，而这也是这种情况下的唯一选择。因为类别量表并没有测量的顺序与距离，因此我们无法用平均数与中位数来描述整个分布。

当然，如果数据是等距或等比量表，那么众数往往不是最优方案。

有些情况下，计算离散变量的平均数会得到一个不可能由离散变量取得的值。

比如我们统计每个家庭的小孩个数和房间个数，如果计算平均数，很可能得到这样的情况：“据统计每个家庭平均有2.4个小孩和 5.33个房间”。但很显然，小孩不能是 2.4 个，房间也不能是 5.33 间。但如果我们使用众数来表达这个分布，就很可能得到“一个典型的家庭有两个小孩和5间房” 这样的结论。

因此可以看出，在数据是离散变量的情况下，众数更能准确的表达分布，因为人们往往比较适应用真实、完整的值来诠释分布，而这种值是可以由众数带来的。

因为众数几乎不需要计算就能获得，所以它一般会在有平均数或中位数的情况下也作为补充信息列出。在频数分布图表中，众数对应的一定是图形的最高峰，所以知道了众数就能大致知道分布的图形，而平均数本身并不能体现这样的信息。

根据美国心理学会（American Psychological Association, APA）指定的学术论文期刊的格式标准：

• $M$ 表示平均数
• $Mdn$ 表示中位数
• 没有专门的符号表示众数。

通常我们也使用图表来表示集中趋势。使用图表的优势是我们可以同时参考几张图中的集中趋势，从而可以快速的比较不同组之间的情况。图的形式有：线性图、直方图和柱状图。

作图的时候有两个要点需要注意：

• 图的起点（零点）不应与坐标系的原点重合。
• 图的高度应该处于图的长度的三分之二到四分之三之间。

因为集中趋势的三种形式都是为了描述分布，因此在某些分布下，三种情况可能相等，而某些情况下可能不相等。而通过分布的形状，我们是可以确认这三种情况是否相等，以及其大小情况的。

前面提到过，对称分布是图形的右侧完全是左侧的镜像的分布。如果一个分布式完美对称的，那么该分布的平均数、中位数会均属于分布对称轴处，也就是分布的中心。而众数的位置需要根据该对称分布的类型来判断：

• 如果该分布只有一个众数，那么众数与中位数，平均数所处同一个位置。
• 如果该分布是 Bimodal Distribution，那么众数离中心的距离不定。
• 该分布也可能没有众数，即所有取得的频数一致。

在偏态分布中，尤其是连续变量的偏态分布，平均数、中位数、众数有很大的可能处于分布中不同的位置。根据偏态分布的正负，可以得出两种情况：



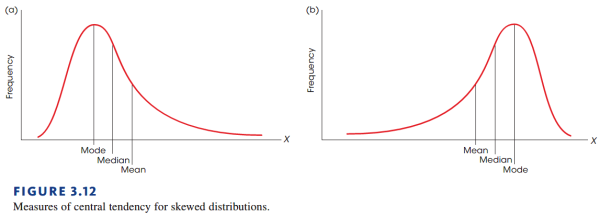
从上图可以看出：

• 正偏态分布下：众数 < 中位数 < 平均数
• 负偏态分布下：平均数 < 中位数 < 众数

这个非常好理解。

1. 众数一定是处于分布的最高点的，因此正分布下必然靠左，负分布下必然靠右
2. 中位数需要将整个分布平均分成两半，那么正分布中会右于众数，负分布中会左与众数
3. 平均数容易受极端分数的影响，因此往往更靠近频率低，但分数非常高的一端。正分布中是右边，负分数中是左边。

• 本章所有参考图来自行为统计学一书