MITx 6.431x notes Unit.1

建立概率模型分为两个步骤：

• 描述所有可能的结果
• 描述所有结果的可能性

Sample space 描述的是一个包含了所有可能结果的 set，记作 $\Omega$

• 结果的独立性（Mutually exclusive），即最终只会出现一个结果
• 结果的有穷性（Collectively Exhaustive），即 set 中所有的元素代表了所有可能得结果

在 sample space 中，如果两个元素之间所有相关的层面（relevant aspects）上均不同（互斥），那么可以称这两个元素为 Physically different outcomes。选取 sample space 应该基于 Physically different outcomes。比如下面的 sample space：

//sample space 1:
硬币朝上
硬币朝下

//sample space 2:
硬币朝上，天下雨
硬币朝上，天不下雨
硬币朝下，天下雨
硬币朝下，天不下雨

sample sampce 分为两种类型：

• 离散型，即元素数量可数
• 连续型，即元素数量不可数

离散型的的 sample space 有两种描述方式：

• 网格表示法
• 树形表示法

比如描述表示扔两次四面骰子（每次 4 种）的所有结果的 sample space：

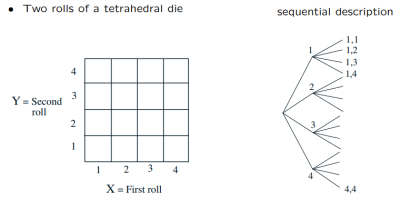
• 网格表示法中，每一个格子代表了一种可能的结果。需要注意的是，不同的顺序代表了不同的结果，比如 (2,3) 代表投 2 再投 3，而 (3,2) 则是 投 3 再投 2
• 树形表示法中，节点代表了阶段 (stage)，而终点（也被称为 leave）被视作当前阶段下的最终结果。所有的结果可以通过 stage 与 leave 的组合表示出来。

连续型的 sample space 存在着无限多的元素，因此通常使用区间来表示。比如下面的例子：


任何方形区域中的结果都可以用 $(x,y)$ 表示（$x,y$ 为实数）

与离散型的 sample space 不同，连续型的 sample space 拥有无限的精度，因此基于某个确切点（元素）的概率为 $0$。因此，在正式的描述中，概率的表示以 set 为单位。该单位被称为 Event，每个 event 都是 sample space 的子集。Event 使用大写的字母标记（比如 $A$），而概率被记作 $P(A)$。

描述过程中，如果某个结果出现，则称描述该结果的 Event 出现。

概率的三大公理：

• 概率不能为负（Nonnegtivity)：$P(A) \geq 0$
• 概率的范围为 $[0,1]$（Normalization），$1$ 代表了所有的结果，即：$P(\Omega)=1$
• （有限情况下）叠加定理（Additivity）：如果 $A$ 与 $B$ 没有交集，那么 $P(A∪B) = P(A)+P(B)$

• $P(A) \leq 1$
• $P(\varnothing) = 0$

在 Events 均为独立的（disjointed）的情况下：

• event 与其补集的概率之和为 $1$，即 $P(A)+P(A^c) = 1$
• $P(A∪B) = P(A) +P(B)$ 可以推广到无限多个 disjointed events，即：

$$ P(s_1,s_2....,s_k) = P(s_1)+...P(s_k) $$

• 子集的概率小于等于父集：$if \,\, A ⊂ B, \,\, then\,\, P(A) \leq P(B)$
• 并集的概率等于集合概率之和减去交集的概率：$P(A∪B) = P(A)+P(B)-P(A∩B)$
  • 推广版本：$P(A ∪ B ∪ C) = P(A) + P(A^c ∩ B) + P(A^c ∩ B^c ∩ C)$
• 并集的概率小于等于集合概率之和：$P(A∪B) \leq P(A)+P(B)$

概率的计算分为如下几个步骤：

1. 指定 sample space
2. 指定对应的 probability law
3. 选取需要计算的 event 进行计算

对于离散 / 有限的样本空间，probability law 可以视作对应元素（outcome）的概率。比如之前扔四面骰子的例子，我们可以假设投掷两次骰子得到的每种结果，其概率是相等的。由于有 $4 \times 4=16$ 种结果，因此每种结果的概率为 $\frac{1}{16}$。

如果需要求指定 set 的概率，那么只需要知道该 set 中存在多少个元素，再与每个结果的概率进行相乘就可以。本例中，假设我们要求两次投掷的点之和是偶数的概率，很容易得出满足条件的 set 为 $\text{{1,1}, {1,3}, {2,2},{4,4}, {3,1},{3,3}, {4,2}, {4,4}}$ ，总计 $8$ 个。因此该 set 出现的概率为 $8 \times \frac{1}{16} = \frac{1}{2}$。

在离散/有限的 sample place 中，假设每一个元素（outcome）概率相等的 probability law 被称为 Discrete uniform law。假设 sample place $\Omega$ 包含了 $n$ 个元素，那么每一个元素的概率为 $\frac{1}{n}$。如果 set $A$ 包含了 $k$ 个元素，那么 $A$ 的概率为：

$$ P(A) = k \times \frac{1}{n} $$

连续的 sample space 中需要以 event 作为单位来赋予概率，因此 uniform law 需要以另外的表现方式存在。一种比较好的方式是将 probability law 定义为面积，将 Omega 面积视作为 $1$。对于需要计算的 event，只需要知道该 event 所占的面积，即可得出其概率。

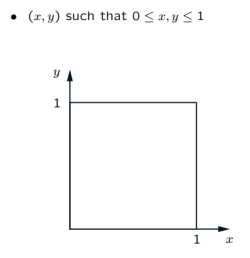
比如下面的例子，可以将 sample space 视作面积为 $1$ 的单位正方形。满足 $x+y \leq \frac{1}{2}$ 的 event 的概率实际上是 $x+y=\frac{1}{2}$ 围成的三角形的面积：

除了以上两种情况，我们还会遇到一种 sample place 是离散的，但又是无限的情况。来看看下面的例子：

假设我们对一个硬币无限次的进行投掷，那么最终投掷到正面的概率是多少?

该例子中，有两个重点：

• 硬币会被无限次投掷，也就是说 event 是无限的
• 硬币投掷是按次数计算的，也就是说 event 是离散的

那么实际上该例子可以被描述为如下的图像：


其中提出的 probability law 为 $\frac{1}{2^n}$。

那么，此类型的例子应该如何计算概率呢？从直觉上来说，我们应该利用有限 / 离散中的 addtivity axiom 性质来处理这种情况。比如我们想统计所有偶数次硬币投掷向上的概率，则可得：

\begin{align} P(outcome\,\,is\,\,even) & = P(\text{{2,4,6...}} )\\ & =P(\left \{2 \right \}\cup \left \{4 \right \}\cup \left \{6 \right \}...)\\ &=P(\left \{2 \right \}) +P(\left \{4 \right \})+P(\left \{6 \right \})...\\ &= \frac{1}{2^2}+ \frac{1}{2^4}+ \frac{1}{2^6}...\\ &= \sum_{n=1}^{\infty}\frac{1}{2^{2n}}\\ &= \frac{1}{2^2}\sum_{n=0}^{\infty}(\frac{1}{2})^{2n}\\ &= \frac{1}{4} \times \frac{1}{1-\frac{1}{4}}=\frac{1}{3} \end{align}
但这里有一个问题，infinite additivity axiom 中并没有说明离散但连续的 sample space 可以使用此类性质。实际上，概率论中对此做出了公理上的扩充用于解决此类问题。该公理被称为 Countable additivity Axiom，定义如下：

if $A_1, A_2, A_3,...$ is an infinite sequence of disjoint events,
then
$$P(A_1 ∪ A_2 ∪ A_3 ∪ ··· ) = P(A_1) + P(A_2) + P(A_3) + ··$$

上面的公理中，有一个条件非常重要：Sequence。这个条件意味着整个样本空间是无限的，但是是可记数（countable）的。那么到底什么样的 sample space 才是可记数的？

总的来说，任意可以排列为序列的元素，都是可记数的。比如自然数，整数等等。作为反例，点 / 线 等等连续的，作为无限细分的单位（由无限细分的单位组成的）元素，都是不可计数的。Countable additivity Axiom 对于此类 sample space 不适用。

• 当 sample space 可记数时，probability 通常被视作频率（frequncy）
• 当 sample space 不存在记数时，probability 也被视作 Description of beliefs，或是 betting preferences，也就是我们到底有多相信该 event 会发生

• 有限的 set 使用大括号：$\{a,b,c,d\}$
• 无限的 set 使用特定的标记：$R: real number$

• 元素 $x$ 属于/不属于 set $S$：
  • 符号：$x \in S$ / $x \notin S$。
  • latex: \in \ \notin
  • 记录方法：元素与 set 的关系，加上元素需要满足的性质，比如 $\{x \in R:cos(x)>\frac{1}{2}\}$

• 全集：$\Omega$
• 补集（complement）：$S^c$，$x\in \Omega, \,x\notin S$
• 空集：$\varnothing$

• S 为 T 的 subset: $S \subset T $
  • $S$ 中的元素也是 $T$ 中的元素
  • $S$ 可能与 $T$ 相等（也可以表示为 $\subseteq$）

• 符号：并集（union）: $\cup$，交集（intersection）：$\cap$
• latex: \cup, \cap

并集的补集等于补集的交集，交集的补集等于补集的并集。 $$ \qquad \displaystyle {\Big(\bigcup _ n S_ n\Big)^ c=\bigcap _ n S_ n^ c,\qquad \Big(\bigcap _ n S_ n\Big)^ c=\bigcup _ n S_ n^ c} $$

Sequences 指一系列的，被自然数索引的元素组成的集合。元素本身可以是各种各样类型的数据（实数，欧式 n 维空间中的值，或者是其他的 set 等等）。Sequences 中的单位通常以大括号加上元素的方式书写，比如 $\{a_i\}$ 正式的定义将 Sequences 视为一个函数：该函数读入对应元素的索引值，即可获得对应元素的值，即：

\begin{align} f:\mathbb{N} \to S \\ f(i)=a_i \end{align}

简单数学定义：sequence 的收敛（Convergence），指 sequence $a_i$ 在 index $i$ 趋于无穷大时，自身总和 $a_i$ 趋于一个指定的值 $a$，即： $$ \displaystyle \lim_{i\to\infty}a_i=a $$ 可以看出来，sequence 的收敛实际上是在看该数列是否在 index 趋于无穷大时存在极限。因此，上述的定义如果用极限定义的方式可以表示为：

For any $\epsilon >0$, there exists $i_0$, such that if $i \geq i_0$, then $$|a_i-a|<\epsilon$$

也就是说，当 sequence 的长度达到一定限度以后，如果 sequence 的值会再以 $[a-\epsilon,a+\epsilon]$ 的这个范围变化的话，那么该 sequence 的极限为 $a$，换句话说就是收敛于 $a$。

如果 sequence 是收敛的，那么：

• $a_i+b_i$ 收敛于 $a+b$
• $a_i \cdot b_i$ 收敛于 $a \cdot b$
• 如果 $g$ 是连续的函数，那么 $g(a_i)$ 会于 $g(a)$ 处收敛

条件可以从两种角度来理解：

• 如果 sequences 不是一直在增长的，即 $|a_i-a_{a+i}|$ 趋近于 0，那么可以说该 sequence 是收敛的
• 如果 sequence 的总和与某个点的距离逐渐趋近于 0，那么可以说该 sequence 收敛于该点。

无穷级数被定义为： $$ \sum_{i=1}^{\infty}a_i= \lim_{n \to \infty} \sum_{i=1}^{n}a_i $$ 也就是说，如果存在这样一种无穷数列，其前 $n$ 个元素之和存在极限，那么我们可以说这整个数列是收敛的；换句话说，该数列的（无穷和）是一个 well-defined，收敛的，无穷级数。

某些 sequence 的元素可能会拥有不同的符号。这种情况下：

• 极限可能不存在
• 极限可能存在但根据求和的顺序会得到不同的极限

一个典型的例子就是交错级数，比如下面的例子： $$\sum_{i=1}^{\infty}(-1)^ia_i$$ 这种情况下，如果 sequence 可以表现为非负（绝对值形式），那么我们就可以对其收敛性做出判断。比如上述的例子可以转化为： $$\sum_{i=1}^{\infty}|a_i|$$ 如果该无穷和是有界的（$< \infty$），那么就能说 ${a_i}$ 是 well-defined 的无穷级数