MITx: 18.01.1x Calculus 1A notes

在处理实际问题的过程中，函数的表达式可能会非常复杂。而近似计算则是利用另外一个相对简单的多项式函数去逼近目标函数的某一部分，从而得到指定定义域内（或者某个点的）函数近似值。对于处理一些不可解的函数关系来说，通过利用多项式的特性来进行近似的手段，是非常有效的。近似计算的精度与多项式的阶数有关，比如本章要讨论的线性近似，二次近似，以及以后的泰勒公式。

线性近似（Linear Approximation）的原理是利用原函数某点的切线作为该函数的表达式。在一个变化足够小的范围内，切线代表的函数结果是可以用于表示原函数在该点的值的。线性近似主要讨论的有两种情况：

• When Linear Approximations near $x=0$.
• General representation When Linear Approximations near $x_0$，where $x_0$ is very close to $x$.

对于第一种情况来说，线性近似的表达式可以记做：

$$f(x) \approx f(0) + f'(0)x$$

而对于一般情况来说，已知函数过点 $x_0, f(x_0)$，那么该函数上处于点 $x$ 处的值 $f(x)$ 的线性近似的表达式可以记做：

$$f(x) \approx f(x_0) + f'(x_0)(x-x_0)$$

具体推导过程请查看第三章微分1.1节。

对复合形式的表达式进行线性近似的情况主要分以下三种：

1. 数字列表项目目标函数是两个函数的和
2. 目标函数是两个函数的乘积
3. 目标函数的自变量是其中一个函数

加法和乘法都非常简单，即目标函数的近似结果等于两个函数的近似结果的和或积，比如：


\begin{align} h(x) = f(x) + g(x) \approx &(f(0)+f'(0)x) + (g(0) +g'(0)x)\\\\ h(x) = f(x)\cdot g(x) \approx &(f(0)+f'(0)x) \cdot (g(0) +g'(0)x) \end{align}
第三种情况稍微有些特殊。当一个函数以复合形式 $f(g(x))$ 的形式出现时，通常我们会令 $u = g(x)$。如果希望使用线性近似，那么 $u$ 需要与 $0$ 非常接近。如果可以直接由 $x \to 0$ 推导出 $u \to 0$（比如 $u = kx$），那么计算的方式是：

1. 使用 $u$ 对 $f(u)$ 进行近似计算
2. 再将 $u = g(x)$ 带入到之前的计算结果中

如果不行，则需要考虑 $u$ 在哪种情况下可以推导出 $x \to 0$。这种情况下计算的方式是：

1. 找到当 $x \to 0$ 时，$u$ 对应 $x$ 的表达式：比如 $u \to 1$，当 $x \to 0$ 时， $u = 1 + x$
2. 使用带 $x$ 的表达式进行近似计算
3. 计算完毕之后将 $x$ 对于 $u$ 的表达式带入到计算结果中。最终结果会以 $u$ 为自变量的形式呈现

\[ \begin{align*} (1+x^2)^{-1} &= {(1+u)}^{-1}\\\\ &\approx 1-u \\\\ &= 1-x^2\\\\ \end{align*} \] 此处令 $u = x^2$ 即可进行线性近似。但最终得到的结果是 $1-x^2$。当然， $x^2$ 在 $x \to 0$ 时 等于 $0$，但作为近似的结果，需要尽可能地保留细节，因此此处的 $x^2$ 不需要做进一步的处理。

Suppose that $g(x)$ is a function such that $g(0) = 0$. To find an approximation of a function $f(g(x))$ near $x=0$ , we can take a linear approximation for $f(u)$ and then substitute g(x) in for $u$ .
The resulting approximation is likely nonlinear, but it is still an linear approximation!.
Warning: this only works if $g(0) = 0$ .
$$\displaystyle \displaystyle f(u) \approx f(0) + f'(0)u \qquad \Longrightarrow \qquad f\left(g(x)\right) \approx f(g(0)) + f'(g(0))g(x)$$

误差一般是属于因变量的变化，而该变化量可以通过自变量的变化来求得。通常来讲，如果有 $y =f(x)$，那么我们就可以通过以下关系来求出 $\Delta y$：

$$y + \Delta y = f(x + \Delta x)$$

这样因变量的变化值往往可以用自变量的变化值来表示。并且，在有多个自变量的函数中，我们可以通过近似计算的复合来评估多变量公式带来的误差。

如果线性近似代表的函数 $L(x)$ 同时满足一下两个条件：

• $L(x)$ 过目标函数 $f(x)$ 的某一点
• $L(x)$ 与 $f(x)$ 在该点的导数相同

那么我们称 $L(x)$ 为 $f(x)$ 最佳匹配（Best Fit）。也就是说，线性近似可以被解释为函数在某点的最佳匹配。

通过以上两个信息，我们可以借由切线的方程在一定程度内对目标函数做出近似计算。但这样的计算是不精确的。根据以上两个信息，我们并不能判断目标函数在该点附近的凹凸性（Concavity)。这对于近似的结果来说有很明显的影响：目标函数可能在切线的上方或者下方。而我们知道，凹凸性是可以通过二阶导数来判断的；因此，如果知道了目标函数在某一点的二阶导数值，我们也就可以利用这个信息使近似计算的误差变得更小。这样的近似方法，我们称为二次近似（Quadratic Approximation）。



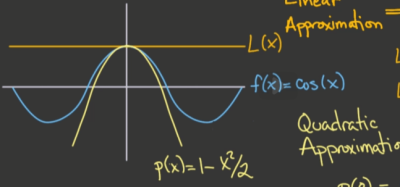
显然的是，二次近似的最佳匹配满足三个条件。假设目标函数为 $f(x)$，二次近似的得到的函数为 $q(x)$，那么在点 $x_0$ 处有：

\begin{align} f(x_0) &=q(x_0)\\\\ f'(x_0) &=q'(x_0)\\\\ f''(x_0) &=q''(x_0) \end{align}

二次近似是用一个二次多项式函数来近似目标函数的。假设我们用于近似目标函数的二次多项式函数为 $f(x) = ax^2+bx+c$。当 $x=0$ 的时候，很容易得出：

\begin{align} f(0) &=q(0)=c\\\\ f'(0) &=q'(0)=b\\\\ f''(0) &=q''(0) =2a\\\\ \end{align}

将上面的 $a,b,c$ 系数以 $f(0)$ 的形式带入二次近似函数，则可得到 $f(x)$ 在近 0 处的近似表达式：

$$\displaystyle f(x) \approx f(0) + f'(0)x + \frac{f^{\prime \prime }(0)}{2}x^2$$
将上面得到的公式中的 0 替换为点 $a$ 并应用到近似的两点形式中，可得：

$$\displaystyle f(x) \approx \underbrace{ f(a) + f'(a)(x-a)}_\text {Linear Approximation} + \underbrace{\frac{f^{\prime \prime }(a)}{2}(x-a)^2}_\text{Quadratic term}$$

如果一个函数由两个函数相乘而得，那么这个函数的二次近似等于组成其函数的二次近似相乘的结果。简单的证明如下：

令$f、g$ 分别为上述的两个组成函数，根据 production rule 有：

\begin{align} (fg)' &= fg' + g'f\\\\ (fg)'' &= f''g + 2f'g' + fg'' \\\\ \end{align}
将$f、g$ 分别代入二次近似公式，并相乘，可得：
\begin{align} Q(f) \cdot Q(g) &= \left(f(0)g + f'(0)x + \frac{f''(0)}{2}x^2\right) \cdot \left(g(0) + g'(0)x + \frac{g''(0)}{2}x^2\right) \end{align}
因为二次近似的乘积最终表现形式也是一个一元二次多项式，因此我们可以将相乘以后高于二次的项都丢弃，整理出来的结果为：

\begin{align} Q(f) \cdot Q(g) & \approx f(0) \cdot g(0) + \left(f'g(0) +fg'(0) \right)x + \left( \frac{fg''(0)}{2} + \frac{gf''(0)}{2} + f'g'(0) \right) x^2 \newline & = f(0) \cdot g(0) + \textcolor{red}{( f(0)\cdot g(0))'} \cdot x + \frac{\textcolor{red} {(f(0) \cdot g(0))''}}{2} \cdot x^2 \end{align}

我们来看一个函数：
$$y=(1+x)^5$$
将这个函数展开以后，有：
$$(1+x)^5 = 1+5x+10x^2+10x^3+5x^4+x^5$$
如果求该函数的线性近似，则可得：
$$(1+x)^5 \approx 1+5x$$
如果求该函数的二次近似，则有：
$$(1+x)^5 \approx 1+5x+10x^2$$
当 $x \to 0$ 的时候，随着 $x$ 的减小，误差部分的值会越来越小，直到可以忽略。近似计算就是利用这样的原理。而从表现形式上来说，我们就可以将一个多项式写成它自身的近似计算结果加上另外一部分（误差）的形式，即：
$$Function = Approximation + Error$$
那么最后这一部分误差的值，则成为了衡量一个近似计算方法精度的标准了，误差越小，当然精度就越高了。

为了更精确的评估这个精度，我们定义了一个值 $O$ (big-O) 来作为评估的标准。$O$ 的原本含义是数量级（Order of magnitude），在一个 $n$ 阶的多项式中，$O$ 代表了误差的最大值上限；而这个上限可以用一个常数的乘积和该多项式误差的最低项所得到的结果再取绝对值表示。因为在 $x$ 足够小的时候，误差的最低项对误差的结果是作用最大的。

<html>

</html>

比如前面的例子，如果是线性近似在 $x=0.1$ 时的 $O$ ，那么就有：
$$O = 10x^2+10x^3+5x^4+x^5$$
可以注意到上面的式子中，$x^2$ 项决定了整个误差的大小。比如将 $x=0.1$ 带入计算，发现这个值是小于 $12x^2$。

当 $x$ 足够小时，高于近似计算最高项的项都可以忽略不计；也就是说，对于不同的多项式，我们都可以找到对应的常数 $k$，使得多项式小于等于其误差的最低项与 $k$ 相乘的绝对值。因此，$O$ 的自变量，代表了这个近似计算精确度的数量级；比如上述的线性近似的精度数量级就是$x^2$ 级别的，记做 $f(x) = O(x^2)$。正式的定义如下：

A function $f(x)$ is on the order $x^n$ near $x=0$, which is denoted using big “O“ notation as $f(x) = O(x^n)$ near $x=0$, if $\left|f(x)\right| \leq k x^ n$.

之前提到的两种近似方案都需要近似点与目标点足够接近。但当需要对目标函数的根，也就是目标函数与 $x$ 轴的交点位置进行近似时，由于我们并不确定该点与近似点的距离有多远，使用传统的近似方法可能会带来较大的误差。这种情况下，需要利用到牛顿方法。



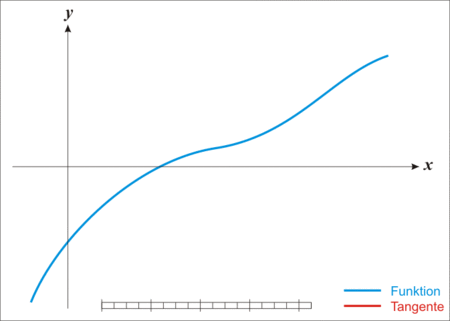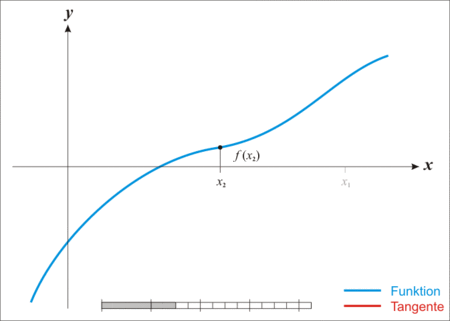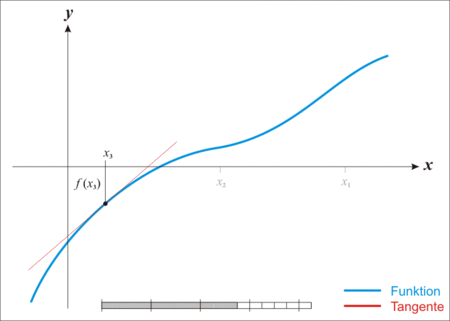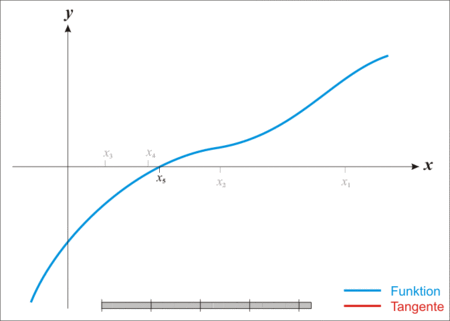
图片来源：Wikipedia，作者：Ralf Pfeifer

从上图可以看出，牛顿法的原理是反复利用线性近似去使得近似点逐渐逼近目标函数与 $x$ 轴的焦点。其核心内容主要是在重复做两件事：

• 确定函数上一点，计算过该点的切线方程，以及该切线方程与 $x$ 轴的交点
• 以该交点的 $x$ 坐标为基础，寻找到函数上对应的点，根据该对应的点求出过该点的切线，并继续求该切线与 $x$ 轴的交点

这两步会反复的进行，直到我们发现得到的切线与 $x$ 的交点会处于非常稳定（收敛）的一个值，那么就可以确认得到的近似值非常接近函数的根值了。

1. 先猜测一个值 $x_0$。
2. 通过这个 $x_0$ 得到对应目标函数上的点，并通过该点对目标函数做线性近似。
3. 通过得到的线性近似方程求解（与 $x$ 轴的焦点）
4. 将求到的解作为新的猜测值，重复以上步骤，直到解收敛。

假设目标函数的方程为 $f(x)$，起始的猜测点为 $x_0$，那么该方程在 $x_0$ 处的线性近似方程为：
$$f(x) = f(x_0) + f'(x_0)(x-x_0) $$
因为我们需要求线性近似方程的解，因此令 $f(x) = 0$，则有：
$$f(x_0) + f'(x_0)(x-x_0) = 0$$
通过该等式求 $x$，即可得到牛顿迭代法的公式：

$$ \displaystyle x_1 = x_0 - \frac{f(x_0)}{f'(x_0)} $$

考虑到我们需要反复应用该等式来逼近正确的解，因此可以将该方程写成：

$$ \displaystyle x_{n+1} = x_ n - \frac{f(x_ n)}{f'(x_ n)} $$

判断牛顿迭代法的收敛条件可以从误差着手。当误差越来越逼近 $0$ 的时候，我们就可以认为算法是收敛的。

假设从第一步开始；为了观察误差的变化，我们需要两个误差值，即第一次计算的误差 $ \epsilon_0$ 和 第二次计算的误差 $\epsilon_1$。令方程真正的解为 $x^*$，则有：

• $ε_0 = x^* - x_0$
• $ε_1 = x^* - x_1$
• $f(x^*) = 0$

通过前一节 $O$ 的相关知识（线性近似），可知误差的 Order of magnitude 为 $x$ 的平方：

\begin{align} f(x^*) &= f(x_0) + f'(x_0)(x^* - x_0) + O((x^*-x_0)^2)\\\\ &=f(x_0) + f'(x_0)ε_0 + O(ε_0^2) \end{align}
因为 $f(x^*) = 0$，因此有：
\begin{align} f(x_0) + f'(x_0)ε_0 + O(ε_0^2) = 0\\\\ f(x_0) = -f'(x_0)ε_0 + O(ε_0^2) \tag{3.1} \end{align}

再通过牛顿迭代法，我们可以得到 $x_1$ 的值如下：
$$ x_1 = x_0 - \frac{f(x_0)}{f'(x_0)} $$
那么 $ε_1$ 的值就可以写成如下形式：

\begin{align} ε_1 &= x^* - x_1\\\\ &= x^* - \left(x_0 - \frac{f(x_0)}{f'(x_0)} \right)\\\\ &= x^* - x_0 + \frac{f(x_0)}{f'(x_0)} \tag{3.2} \end{align}

将先前得到的公式 3.1 带入 3.2，则有：

\begin{align} ε_1 &= x^* - x_0 + \frac{f(x_0)}{f'(x_0)}\\\\ &=ε_0 + \frac{-f'(x_0)ε_0 + O(ε_0^2)}{f'(x_0)}\\\\ &=ε_0 - ε_0 + \frac{O(ε_0^2)}{f'(x_0)}\\\\ &=O(ε_0^2) \end{align}

根据这个结果可以推导出，$ε_n = O(ε_{n-1}^2) = O(ε_{n-2}^4)...$，也就是说误差在以 $x^2$ 的规模减小，也就是收敛程度为二阶。

不收敛的情况大概分四种：

1. 误差越来越大
2. 循环震荡的不收敛，即 $f(-x) = -f(x)$，也就是 $x_{n+1} = -x_n$
3. 猜测点位于驻点（$f'(x_n)$ 太小，导致得到的解太大。图像上为切线几乎与 $x$ 轴平行）
4. 不能完整求出所有的根

• 挑选方程式，要近似的对象最好为方程的根
• 方程的挑选要避免要避免 $f(x) = f'(x) = 0$ 这类情况。这类情况下，误差收敛的速度会非常慢
• 选择初始猜测点时，该点的导数在函数上的斜率不能太“平”（靠近 $x$ 轴）。太平会使得到 root 太大，导致近似的结果偏移到另外一个 root，或是无法收敛

某些函数表现为 $\frac{p(x)}{q(x)}$ 的形式。这种情况下需要有两点要注意：

• 看题目要求的近似是什么数量级。这一点非常关键，因为涉及到商时，数量级本身也会进行相除。比如，$p(x)$ 是线性近似，$q(x)$ 也是线性近似，那么相除之后得到的是常数级的近似结果，而不是线性近似。
• 近似的商不等于商的近似

来看一个典型例题：

Find the linear approximation of $\displaystyle \frac{\ln (1+x)}{xe^x}$ near $x = 0$

这道题同时具有上述的两个坑。首先我们会想到的是算出 $ln(1+x)$ 和 $e^x$ 的线性近似，然后相除，也就是 \begin{align} \displaystyle \frac{\ln (1+x)}{xe^x} &\approx \frac{x}{x\cdot (1+x)} \newline &= \frac{1}{x+1} \end{align} 这样做显然是错误的。首先，分子与分母都是线性近似的结果，相处以后得到的近似结果是常数级别的；但本题要求的是线性近似。其次，由于线性近似的乘积等于乘积的线性近似，对于 $e^{-x}$，该近似结果不能直接进行相除，而是要转化为乘积的形式进行再次近似，最终得到的结果才能使用。因此正确的求解有两个要点：

• 对 $ln(1+x)$ 进行二次近似，保证商之后得到的结果时线性级的
• 转化$1/e^x$ 的结果为乘积形式，并再次进行线性近似

\begin{align} \displaystyle \frac{\ln (1+x)}{xe^x} &\approx \frac{{\color{red} x+\frac{x^2}{2}} }{x\cdot (1+x)} \newline &= \frac{1+\frac{x}{2} }{x+1} \newline &= (1+\frac{x}{2}) \cdot(x+1)^{-1} \newline &\approx (1+\frac{x}{2}) \cdot{\color{red} (1-x)} \newline &=1- \frac{3}{2} x \end{align}

• 如何通俗易懂地讲解牛顿迭代法求开方？