MITx: 18.01.1x Calculus 1A notes

理解极限可以从无穷数列开始。

我们在高中的时候见过不少的无穷数列。其中的一些无穷数列收敛于一个实数 $L$。我们通常把 $L$ 称为该数列的极限。

而数列本身可以看做是自然数到实数 $N \to L$ 的一个函数；因此我们就可以把极限的概念从数列转到函数上：当函数的自变量 $n$ 趋近于 $\infty^+$ 的时候，$f(n)$的值无限趋近于 $L$。

在刚提到的无穷数列所表达的函数中， 数列函数的自变量 $n$ 是无限趋近于 $\infty^+$ 的。我们来试想一下如果 $n$ 的值无限趋近于一个数列上某一个点 $a$ 的情况下，那么函数的极限又会怎么样呢？

结果很好猜测。我们把 $a$ 代入函数，得到的结果是 $f(a)$。因此不难得出，当 $n \to a$ 的时候，是有 $f(x) -> f(n)$的。

看起来好像 $f(n)$ 应该是数列在 $a$ 点的极限了。不过这里又有另外一个问题。在数列中，我们的 $n$ 到底是在 $a$ 的左边还是右边？这两种可能性导致了我们需要考虑两种情况：$n$ 从左边或者右边无限趋近于 $a$，也就是说，我们的 $f(n)$ 也有两种情况，即在 $a$ 的左边或者右边。因此，对数列上的一个点我们实际上有两个极限：左极限和右极限。

根据上面的推理我们可以描述一下左极限和右极限的定义：



右极限可以被定义为：

Suppose $f(x)$ gets really close to $R$ for values of $x$ that get really close to (but are not equal to) a from the right. Then we say $R$ is the right-hand limit of the function $f(x)$ as $x$ approaches $a$ from the right.

记做：$\displaystyle {\lim _{x\rightarrow \mathbf{a^+}} f(x) = R}$

左极限的定义类似：

If $f(x)$ gets really close to $L$ for values of $x$ that get really close to (but are not equal to) a from the left, we say that $L$ is the left-hand limit of the function $f(x)$ as $x$ approaches a from the left.

记做：$\displaystyle {\lim _{x\rightarrow \mathbf{a^-}} f(x) = L}.$

判断一个极限是否存在，首先要明白：函数 $f(x)$ 在 $a$ 点的极限，指的是当 $x$ 从左右同时趋近于 $a$ 时的极限。只有当 $f(x)$ 在 $a$ 点的左极限和右极限存在且相等时候，我们才说，函数的极限存在： $$\displaystyle {\lim _{x\rightarrow a^+} f(x)} = \displaystyle {\lim _{x\rightarrow a^-} f(x)} = L$$ then $$\displaystyle {\lim _{x\rightarrow a} f(x) = L}$$

• 左极限和右极限存在，但不相等
• 左右极限可能趋向于无穷大，无穷小
• 左右极限可能会在某个区间内震荡（比如 sinx)

我们也来看看正式的数学定义：

For all $ε>0$, there exists some $δ>0$ such that if $0<|x−a|<δ$, then $|f(x)−L|<ε$.

来看看这个公式里都有什么新的：$ε$, $δ$。这两个量是作为距离的描述：

• $ε$ 描述 $f(x)$ 到 $L$ 的距离 。
• $δ$ 描述 $x$ 离 $a$ 的距离。

总的来说，这两个量用于描述一个非常小的距离：

1. $0<|x−a|<δ$ 代表 $x$ 到 $a$ 的距离处于一个非常小的范围 $δ$ 内。
2. 同理，$|f(x)−L|<ε$ 表明 $f(x)$ 到 $L$ 的距离也处于一个非常小的范围 $ε$ 内

证明极限存在需要满足上述的这两个表达中的：

• $ε$ 可以是任意值
• $ε$ 可以通过任意的，与 $a$ 点距离小于 $δ$ 的 $x$ 来满足，也就是通过 $x$ 总是可以得到 $f(x)$，其与极限值 $L$ 的距离始终小于 $ε$。

极限可以做 +、-、*、/ 运算。

假设我们有：$\displaystyle {\lim _{x\rightarrow a} f(x) = L}$，$\displaystyle {\lim _{x\rightarrow a} g(x) = M}:$，则：

• $\displaystyle {\lim _{x\rightarrow a} \left[f(x)+g(x)\right] }$ $=$ $L+M$：和的极限是极限的和。
• $\displaystyle {\lim _{x\rightarrow a} \left[f(x)-g(x)\right] }$ $=$ $L-M$：差的极限是极限的差。
• $\displaystyle {\lim _{x\rightarrow a} \left[f(x)\cdot g(x)\right] }$ $=$ $L\cdot M$：乘积的极限是极限的乘积

（以加法为例子）： 假设有 $\displaystyle {\lim _{x\rightarrow a} f(x) = L}$ 和 $\displaystyle {\lim _{x\rightarrow a} g(x) = M},$，可知：
$$\begin{align*} f(x) = L + \varepsilon_1 \\ g(x) = M + \varepsilon_2 \\ \end{align*}$$

因此，有 $$f(x) + g(x) = L + M + \varepsilon_1 + \varepsilon_2$$

当 $x \to a$ 时，$\varepsilon_1, \varepsilon_2 \to 0$，因此

$$\displaystyle {\lim _{x\rightarrow a} \left[f(x)+ g(x)\right] } = L + M$$

同理可证其他的极限定理。

当在 $x=a$ 的时候，如果有 $\displaystyle {\lim _{x\rightarrow a} f(x) } = f(a)$，则我们称函数 $f(x)$ 在点 $a$ 处连续（Continuous）。显然，$f(x)$ 在 $a$ 处连续时，极限是非常好计算的。

连续也分左右：

• 如果 $\displaystyle {\lim _{x\rightarrow a^+} f(x) } = f(a)$，那么我们称 $f(x)$ 在 $a$ 点右连续。
• 如果 $\displaystyle {\lim _{x\rightarrow a^-} f(x) } = f(a)$，那么我们称 $f(x)$ 在 $a$ 点左连续。

如果函数 $f$ 在其定义域上的所有点都连续，则称该函数 $f$ 是连续的。这种类型的连续也被称为 Overall continuity。

• 常见的连续函数有：
  • 所有的多项式
  • $\cos x$ 和 $\sin x$
  • $a^x$ 当 $a > 0$
  • $\sqrt [3]{x}$，$|x|$
• 带条件的常见连续函数有：
  • $\log _{a} x$ 当 $a > 0$、$x > 0$
  • $\tan x$ 在所有定义过的 $x$ 上
  • $\sqrt {x}$ 当 $x>0$。

上面的函数很多都可以表示为函数运算的的形式。我们可以利用来证明函数连续性是与单个函数的连续性相关（以乘法为例子）： 假设有$f(a)$， $f(b)$ 在实数定义域上连续。根据连续的定义，可得：$\displaystyle {\lim _{x\to a} f(x) } = f(a)$ 且 $\displaystyle {\lim _{x\to b} f(x) } = f(b)$。

由 $\displaystyle{\lim _{x\rightarrow a} \left[f(a)\cdot g(b)\right] } = {\lim _{x\to a}f(a) \cdot {\lim _{x\rightarrow b}f(b) } = f(a) \cdot f(b) }$，可知复合函数$f(a) \cdot f(b)$ 也是连续的。该证明可以推广到加法和减法，以及复合函数。

除法的话，只在 $f/g$ 有定义的区域连续。

当然，如果$\displaystyle {\lim _{x\rightarrow a} f(x) }$ 或者 $f(a)$ 不存在，那么很显然 $f(x)$ 在 $a$ 点是不连续的。而不连续（Discontinuity）大概分两种种类：Jump discontinuity 和 Removable discontinuity 。

如果 $f(x)$ 在点 $a$ 的左右极限都存在但是不相等，我们就称 $f(x)$ 在点 $a$ 是 Jump discontinuity。


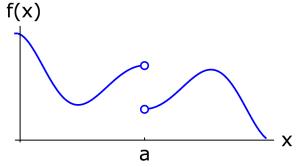
如果 $f(x)$ 在点 $a$ 的左右极限都存在且相等，但 $f(a)$ 不存在，我们就称 $f(x)$ 在点 $a$ 是 Removable discontinuity。

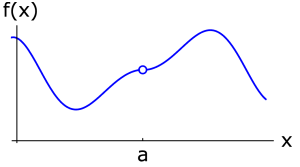
介值定理（Intermediate Value Theorem）的定理如下：

If f is a function which is continuous on the interval $[a,b]$, and $M$ lies between the values of $f(a)$ and $f(b)$, then there is at least one point $c$ between $a$ and $b$ such that $f(c)=M$.

$f(c)=M$ 意味着 $f$ 与 $M$ 代表的直线相交。那么这样就好理解了，如果有两个点分别处于 $y=M$ 的上下方，且通过该两点的函数是连续的，则该函数必与 $M$ 必至少有一个交点。

几个需要注意的点：

• 区间的限定：$[a,b]$，也就是 $f$ 在 $a$ 点右连续，在$b$点左连续，在 $[a,b]$ 上连续
• 我们通常令 $M = 0$, 这样函数就成为了一个方程了。只要该函数在某个区域连续，且该区域内两点处函数值一正一副，那么该方程在该区域内必然有根。
• 介值定理只能应用于连续的函数上，而介值定理也只能判定根的存在性，并不能判定根的具体数量。

极限的商分好几种情况：

1. 如果 $M \ne 0$, 则 $\displaystyle { \lim _{x\rightarrow a} \frac{f(x)}{g(x)} = \frac{L}{M}}$
2. 如果 $M=0$ 但 $L \ne 0$, 则 $\displaystyle {\lim _{x\rightarrow a} \frac{f(x)}{g(x)}}$ 不存在（DNE）。
3. 如果$M=0$ 且 $L=0$, 则 $\displaystyle {\lim _{x\rightarrow a} \frac{f(x)}{g(x)}}$ 可能存在，也可能不存在，需要进一步的判断（比如对多项式做因式分解）。

如果函数是连续的，直接求分母分子在该点的值即可。该值等于函数在该点的极限，相除之后则是结果，比如：

$$\displaystyle {\lim _{x\rightarrow 0} \frac{x^+2x-3}{x^2-3x+2} } = \frac{-3}{2}$$

可以采取的策略是，简化函数，使其满足分子分母都不为 0 的形式，比如多项式可以通过因式分解： $$\begin{align*} \displaystyle {\lim _{x\rightarrow 1} \frac{x^2+2x-3}{x^2-3x+2} } &= {\lim _{x\rightarrow 1} \frac{(x-1)(x+3)}{(x-1)(x-2)} } \\ &= {\lim _{x\rightarrow 1} \frac{x+3}{x-2} } \\ &= 4 \end{align*}$$ 如果简化的情况转移到了第二种 $0/~0$ 的情况，则极限不存在。

某些函数的极限可以归类到无穷大 / 无穷小的情况。这种情况下，如果希望知道函数极限的趋势，那么需要从左和右趋近点，来看 overall limit 是否会有一个总的趋势。如果两个方向的趋势不同，则极限不存在。

• summary PDFs：极限 | 连续 | 极限的商