目录
Gaussian Elimination
LAFF Week 6 Notes
本章的主要内容:
- 高斯消元、高斯变换的推导及其算法实现
- LU 分解的推导及其算法实现
- 相关算法复杂度的掌握
Linear Systems & Gaussian Elimination
在中学的时候我们都学习过如何解三元一次方程组。来看看下面三元一次方程组是怎么解的: $$ \left\{\begin{matrix} 2x_0& &+&4x_1 &-&2x_2 &=& -10&\\ 4x_0& &-&2x_1 &+&6x_2 &=& 20& \\ 6x_0& &-&4x_1 &+&2x_2 &=&18& \end{matrix}\right. $$ 解的方法很简单:消元;也就是用方程组内的几个线性关系通过加减、与标量相乘 和等式的顺序变换,可以达到减少未知数的效果。上面的例子,我们可以观察到:
- 第二行加上
-2乘以第一行的结果,可以消去第二行中的 $x_0$ - 第三行加上
-3乘以第一行的结果,可以消去第三行中的 $x_0$
完成上面两步以后,我们的方程组变成了这个样子:
$$
\left\{\begin{matrix}
2x_0& &+&4x_1 &-&2x_2 &= &-10\\
& &-&10x_1 &+&10x_2 &= &40 \\
& &-&16x_1 &+&8x_2 &= &48
\end{matrix}\right.
$$
我们发现第二行和第三行的方程只存在 $x_1$、$x_2$ 两个未知数了。按照之前的方法,我们在将第三行加上第二行乘以 -1.6 的结果,发现可以消除第三行中的 $x_1$。得到的结果如下:
$$
\left\{\begin{matrix}
2x_0& &+&4x_1 &-&2x_2 &= &-10\\
& &-&10x_1 &+&10x_2 &= &40 \\
& && &-&8x_2 &= &-16
\end{matrix}\right.
$$
Appended Matrices
我们可以将上面的方程组写成如下不带未知变量的形式:
$$
\left(
\begin{array}{r r r | r}
2 & 4 & -2 & -10 \\
4 & -2 & 6 & 20 \\
6 & -4 & 2 & -18
\end{array}
\right)
$$
这样的形式被称为 Appended Matrices,这种形式可以更方便的将方程组与矩阵联系起来。让我们把上面这个流程写成该矩阵的形式:
$$
\left( \begin{array}{r r r | r}
2 & 4 & -2 & -10 \\
& -2 & 6 & 40 \\
& -4 & 2 & -48
\end{array} \right)\tag{step.1}
$$
$$
\left( \begin{array}{r r r | r}
2 & 4 & -2 & -10 \\
& -2 & 6 & 40 \\
& & 2 & -16
\end{array} \right)\tag{step.2}
$$
如果我们把每一步消去的未知变量的位置都用 0 填充的话,我们会发现整个消元的过程实际上是目标矩阵变换为一个三角矩阵的过程(此处是上三角矩阵):
$$
\left( \begin{array}{r r r | r}
2 & 4 & -2 & -10 \\
0 & -2 & 6 & 40 \\
0& 0 & 2 & -16
\end{array} \right)
$$
Gauss Transforms
我们再来看看当初将例子中的原矩阵变换为三角矩阵的(以 $L$ 表示方程组的行):
- $L_2 + (-2) * L_1$
- $L_3 + (-3) * L_1$
- $L_3 + (-1.6) * L_2$
现在我们将上面例子中的 Appended Matrices 的左边部分表示为一个单位矩阵与其的乘积:
$$
\left( \begin{array}{r r r}
1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right)
\left(
\begin{array}{r r r | r}
2 & 4 & -2 & -10 \\
4 & -2 & 6 & 20 \\
6 & -4 & 2 & -18
\end{array}
\right)
$$
如果我们注意观察的话,我们第一步和第二步是需要消除第二行和第三行中的 $x_0$。先来看看第二行,这里发生的点积如下图:
<html>
<img src=“/_media/math/linear_algebra/laff/gs_tr.svg” width=“600”>
</html>
消除第二行中 $x_0$,也就是将目标矩阵中第二行中 $x_0$ 的系数置零。在计算该系数的点积中,我们只需要将单位矩阵中参与点积运算的第二行的第一个元素修改,使其与 2 的乘积与第二行 $x_0$ 系数
-4 之和为 0 即可,也就是通过修改单位矩阵第二行第一个元素,保证单位矩阵第二行与目标矩阵第一列点积为 0 即可。
因此我们能得到上图粉色区域的关系,从而轻松的求到一个 multiplier(粉色区域的 ? ),也就是我们之前在高斯消元中用第二行和第一行消除 $x_0$ 需要用到的系数。而这个系数恰好能放到单位矩阵对应的位置中。
依次类推,第三行与第一行消除 $x_0$、第三行与第二行消除 $x_1$ 的系数,我们都可以放置到这个单位矩阵中。因此我们可以用如下的矩阵乘法来表示之前高斯消元的整个过程:
$$
\left( \begin{array}{r r r}
1 & 0 & 0 \\
\frac{-4}{2} & 1 &0 \\
\frac{-6}{2} & -\frac{-16}{-10} & 1 \end{array} \right)
\left(
\begin{array}{r r r | r}
2 & 4 & -2 & -10 \\
4 & -2 & 6 & 20 \\
6 & -4 & 2 & -18
\end{array}
\right)
$$
Forward Substitution
我们再观察作为结果的最右边的部分。在之前的高斯消元法中,我们每进行消除一个未知数的步骤,都需要同时更新最右边方程组的结果部分。
而在高斯变换中,我们得知了如何用一个矩阵来表示整个目标矩阵消元的过程。因此对于代表方程组结果的向量,我们并不需要每次更新,只需要在得到消元过程的矩阵之后,将其与目标矩阵中最右边代表结果的向量做矩阵乘法,就可以得到消元以后代表方程组结果的新向量。以上面的例子可以表示为:
$$
\begin{pmatrix}
1 & 0 & 0 \\
\frac{-4}{2} & 1 &0 \\
\frac{-6}{2} & -\frac{-16}{-10} & 1
\end{pmatrix}
\begin{pmatrix}
-10 \\
20 \\
-18
\end{pmatrix}
=
\begin{pmatrix}
-10 \\
40 \\
-16
\end{pmatrix}
$$
我们将这种把高斯变换直接应用到目标矩阵的最右边部分的运算称为 Forward substitution.
高斯变换的算法设计
在计算机中,算法的设计与数学上的推理有一些差异。这种差异主要体现在计算机算法的设计要尽量的节省对内存的读取。下面来看看高斯变换的设计过程。
首先我们再次确认下目标:我们需要通过高斯变换将目标矩阵转化为一个上三角矩阵。根据之前高斯变换部分的推导可以发现,每次迭代中我们都需要消除一个变量;也就是说,每次对单位矩阵的更新是一个列向量。因此,我们采用四象分割法来对矩阵进行处理。
其次,我们来看一下单位矩阵中需要更新的 multiplier 与目标矩阵中向量之间的关系。根据之前推导的结果很容易发现, multiplier 与目标矩阵中向量的关系(以之前的例子为例):
<html>
<img src=“/_media/math/linear_algebra/laff/gs_al_step_1_r.svg” width=“350”>
</html>
当我们得到了消除 $x_0$ 的向量,我们需要使用该向量消除目标矩阵中需要被消除 $x_0$ 系数的行,本例中应该是目标矩阵中第一列第二、三行的第一个元素,也就是上图中的 A21:
<html>
<img src=“/_media/math/linear_algebra/laff/gs_al_step_2.svg” width=“450”>
</html>
而此时为了节省空间,我们发现目标矩阵中已经被我们消除了 $x_0$ 系数向量($A_{21}$)的位置全是 0,因此我们可以利用该位置来存储单位矩阵中高斯消元的记录(上图第三个矩阵)。
这里需要注意的是,单位矩阵中存放的高斯消元的步骤向量,是需要求负的,这样算出结果才正确。但如果将该步骤向量存放到目标矩阵中,则不需要加负号了(课程中也没有详细说明,个人猜测应该是默认操作为减法)
应用了高斯变换之后,我们需要更新一下我们的目标矩阵,而更新的方法很简单,直接使用更新单位矩阵对应列与目标矩阵的对应行点积就可得到目标矩阵中更新后的元素即可。下图的演示过程是目标矩阵中最正中心的元素 -2,更新之后值变为 -10:
<html>
<img src=“/_media/math/linear_algebra/laff/gs_al_step_3.svg” width=“450”>
</html>
利用更新后的单位矩阵将目标矩阵更新(也就是更新的单位矩阵乘上目标矩阵)后,再存储上高斯变换的步骤,我们就可以得到新的目标矩阵:
$$
\begin{pmatrix}
2 & 4& -2\\
2 & -10 & 10\\
3 & -16 & 8
\end{pmatrix}
$$
到此我们完成了第一轮循环,也就是消除 $x_0$ 序数的循环。接下来我们接着分割矩阵,进入第二轮消除 $x_1$ 系数的循环。在本例中,本轮是目标矩阵的第二行与第三行进行消除操作。而在经过第二轮的分割,参与运算的目标矩阵如下图:
<html>
<img src=“/_media/math/linear_algebra/laff/gs_al_step_4.svg” width=“350”>
</html>
我们发现第二轮的更新中依然是用对角线元素下方的向量来除以对角线上的元素来获取 multiplier ,也就是:
$$L_{21} = - A_{21} / a_{11}$$
因此,整个算法中对于目标矩阵左边部分的操作,其迭代部分已经非常明显了:
- 通过对角线元素下方的向量来除以对角线上的元素来获取
multiplier - 将更新后的单位矩阵与目标矩阵相乘,得到更新后的目标矩阵
- 通过分割矩阵,接着对子矩阵应用前面两步
当然,我们还记得高斯变换算法中需要对目标矩阵的右边部分进行 Forward substitution。在算法中,我们可以通过每一步迭代中得到的更新的单位矩阵与当前的目标矩阵的右边部分相乘,从而得到更新后的目标矩阵的右部。本步骤在算法中作为独立的一部分算法,在后面会接着讨论。
具体的算法推导
看算法的一个诀窍:把所有下标为 $1$ 的内容想象成当前循环中的内容。
之前的内容中我们已经讨论过高斯消元算法中每次迭代的内容。为了算法设计的方便,我们再来看看这部分迭代内容有什么样的特点。
参考一下之前用单位矩阵表达消元步骤的方法,我们发现在每一步的消元过程中,目标矩阵的对应区域都会归零(也就是通过抵消掉指定变量的系数来消除变量)。
而从输入输出的角度来看,有两点需要注意:
- 输入 / 输出:单位矩阵与目标矩阵 / 上三角与矩阵。
- 单位矩阵自带
multiplier。
根据上面的信息,如果使用四象分割,那么一个高斯变换的迭代部分可以表示为以下的矩阵乘法:
$$
\left( \begin{array}{r | r r}
\color{blue}{I} & 0 & 0 \\
\hline
0 & 1 & 0 \\
0 & \color{red}{-l_{21}} & \color{blue}{I}
\end{array} \right)
\left(
\begin{array}{r | r r}
U_{00} & u_{01} & U_{22} \\
\hline
0 & a_{11} & a_{12}^T \\
0 & a_{21} & A_{22}
\end{array}
\right)
=
\left(
\begin{array}{r | r r}
U_{00} & u_{01} & U{22} \\
\hline
0 & v_{11} & u_{12}^T \\
0 & 0 & A_{22}^{new}
\end{array}
\right)
$$
那么这个算法中每次需要更新的有哪些呢?很显然,是 multiplier 和 子矩阵 A22。因此我们不妨利用这个关系,来看看如何得到 multiplier 和 A22 至于矩阵中其他向量 / 元素的表达式。先将等号左边计算一下:
$$
\left( \begin{array}{r | r r}
\color{blue}{I} & 0 & 0 \\
\hline
0 & 1 & 0 \\
0 & \color{red}{-l_{21}} & \color{blue}{I}
\end{array} \right)
\left(
\begin{array}{r | r r}
U_{00} & u_{01} & U_{22} \\
\hline
0 & a_{11} & a_{12}^T \\
0 & a_{21} & A_{22}
\end{array}
\right)
=
\left(
\begin{array}{r | r r}
U_{00} & u_{01} & U_{22} \\
\hline
0 & \left( \begin{array}{r | r}
1 & 0 \\
\hline
\color{#F0F}{-l_{21}} & \color{#F0F}{I}
\end{array} \right)
& \left( \begin{array}{r | r}
\color{green}{a_{11}} & a_{12}^T \\
\hline
a_{21} & A_{22}
\end{array} \right) \\
\end{array}
\right)
\\
=
\left(
\begin{array}{r | r r}
U_{00} & u_{01} & U_{22} \\
\hline
0 &
& \left( \begin{array}{r | r}
a_{11} & a_{12}^T \\
\hline
\color{red}{-l_{21}a_{11}+a_{21}} & \color{#F0F}{-l_{21}a_{12}^T + A_{22} }
\end{array} \right) \\
\end{array}
\right)
$$
将这个结果与矩阵乘法的右边对应,我们可以得到两个等式:
- $-l_{21}a_{11}+a_{21} = 0$
- $-l_{21}a_{12}^T + A_{22} = A_{22}^{new}$
整理一下:
- $l_{21} = a_{21} / a_{11} $
- $A_{22}^{new} = -l_{21}a_{12}^T + A_{22}$
这里有一点非常重要:我们之前提到过,为了节省空间,我们可以将 multiplier 存放到目标矩阵中。在迭代中,我们可以看到的是 $a_{21}$ 的位置实际上存放了单位矩阵中 $l_{21}$ 的内容。那么这个过程可以描述为两个步骤:
- 使用当前的 $a_{21}$ 计算 $l_{21}$
- 计算完毕之后,将 $l_{21}$ 的值存放到 $a_{21}$ 所在的内存空间中,将 $a_{21}$ 作为 $l_{21}$ 进行矩阵的更新。
因此整个迭代部分的算法就可以写成:
a21 = a21 / a11 //it means l21=a21/a11, then a21 = l21;
A22 = A22 - a21 * a12t // means A22=A22-l21*a12t , rank 1 update
Forward Substitution 的算法设计
Forward Substitution 就是将表示消元步骤的单位矩阵与目标矩阵的右边表示结果的向量相乘,得到与变换后的三角矩阵匹配的结果向量。利用之前的表示方法,我们也可以将该迭代过程表示成如下的矩阵乘法:
$$
\left( \begin{array}{r | r r}
\color{blue}{I} & 0 & 0 \\
\hline
0 & 1 & 0 \\
0 & \color{red}{-l_{21}} & \color{blue}{I}
\end{array} \right)
\left( \begin{array}
y_0 \\
\hline
\color{blue}{\beta_1} \\
\hline
b_2
\end{array} \right)
=
\left( \begin{array}
y_0 \\
\hline
\color{blue}{\chi_1} \\
\hline
b_2^{new}
\end{array} \right)
$$
化简左边以后可以得到:
$$
\left( \begin{array}
y_0 \\
\hline
\color{blue}{\beta_1} \\
\hline
\color{#0F0}-l_{21}\beta{11}+b_2
\end{array} \right)
=
\left( \begin{array}
y_0 \\
\hline
\color{blue}{\chi_1} \\
\hline
b_2^{new}
\end{array} \right)
$$
可以看到的是,每次更新中,只有 $b_2$ 的值发生了更新,也就是每次更新只对结果变量的余下部分造成影响。因此每次迭代的内容实际上就是更新 $b_2$。又因为 $l_{21}$ 实际上就是更新后的 $a_{21}$,因此整个迭代过程可以记做:
b_2 = b_2 - a21b11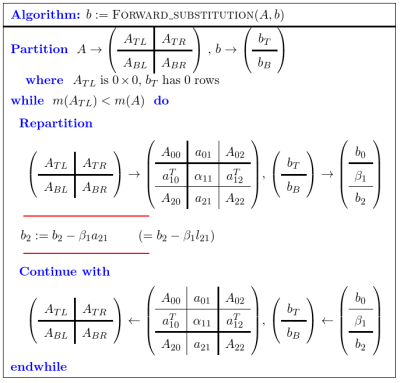
LU factorization
什么是LU分解
先来了解一下 LU 分解的概念:
- $A$ 是一个
n*n的矩阵 - $L$ 是一个
n*n的下三角单位矩阵 - $U$ 是一个
n*n的上三角矩阵
对于以上条件,如果存在 $A = LU$,那么我们就称 $LU$ 是 $A$ 的 $LU$ 分解。
LU 分解的算法
本章这里我们暂且认为 $LU$ 分解就是高斯消元 的一种,在之后的章节里会对这两者的关系作出详细解释。同时,我们也会在后面看到两者几乎拥有一模一样的算法分析步骤及内容。
还是按之前处理高斯变换的四象分割的办法,我们将 $A、L、U$ 分别分割,然后用矩阵乘法表示我们之前提到过的等式 $A=LU$:
$$
\left( \begin{array}{c | c c} A_{00} & a_{01} & A_{02} \\ \hline a_{10}^T & \alpha_{11} & a_{12}^T \\
A_{20} & a_{21} & A_{02}
\end{array} \right) =
\left( \begin{array}{c | c c} L_{00} & 0 & 0\\ \hline l_{10}^T & 1 & 0 \\
L_{20} & l_{21} & L_{02}
\end{array} \right)
\left( \begin{array}{c | c c} U_{00} & u_{01} & U_{02} \\ \hline 0 & \upsilon_{11} & u_{12}^T \\
0& 0 & A_{02}
\end{array} \right)
$$
这里是不是很熟悉,跟之前的高斯变换简直一模一样!而我们注意到了高斯变换中,真正对算法起更新作用的,只有在当前循环所处的分割块的元素(比如什么 $U_{00}$ 的就完全没啥用)。那么对于 $LU$ 分解,假设当前是第一次循环,因此做为上次循环中的元素 $A_{00}$ 为空;也就是说第一次的分割中 $$
\displaystyle \left( \begin{array}{c c} \alpha_{11} & a_{12}^T \\
a_{21} & A_{02}
\end{array} \right)
$$
代表了整个目标矩阵(不清楚可参考 Week.3 1.1)。那么很显然,我们有:
$$
\left( \begin{array}{r | r} \alpha_{11} & a_{12}^T \\
\hline
a_{21} & A_{02}
\end{array} \right) =
\left( \begin{array}{r | r} 1 & 0 \\
\hline
l_{21} & L_{02}
\end{array} \right)
\left( \begin{array}{r | r}\upsilon_{11} & u_{12}^T \\
\hline
0 & A_{02}
\end{array} \right)
\\
=
\left( \begin{array}{r | r} \upsilon_{11} & a_{12}^T \\
\hline
\upsilon_{11} l_{21} & l_{21} u_{12}^T + L_{22} U_{22}
\end{array} \right)
$$
将元素一一对应起来,则能得到以下关系:
- $a_{11} = v_{11}$
- $a_{12}^T = u_{12}^T$
- $a_{21} = l_{21}v_{11}$
- $A_{22} = l_{21}u_{12}^T + L_{22}U_{22}$
从上面关系中,我们发现每次迭代更新的内容依然是 multiplier 和 目标矩阵。不过对于目标矩阵的更新,我们发现这里有一点与之前的高斯变换不同;这里面多了一个 $L_{22}U_{22}$。
如果足够细心,就能明白发现这个矩阵乘积的意义:$L_{22}$ 是一个单元下三角矩阵, $U_{22}$ 是上三角矩阵,他们又各自是 $L$ 与 $U$ 的子矩阵。$A_{22}$ 是我们已知的,$l_{21}u_{12}^T$,也就是 $a_{21}u_{12}^T$,是一个外积,一个相对于 $A_{22}$ 的 rank1 更新,并且也是已知的。那么这一行的意思就很明显了:
- $L_{22}U_{22}$ 实际上代表了 $A_{22}$ 更新以后的内容,也就是更新过后的 $A_{22}$
- $A_{22}$ 通过外积 $a_{21}u_{12}^T$ 更新
那么整个算法的迭代部分就基本可以确定了:
a21 = a21/a11
A22 = A22 - a21a12t
是不是跟高斯消元很像?$L$ 是不是很像我们用于表示消元的高斯变换,$U$ 像不像消元后的目标矩阵?如果还不明白的话,来从头看一遍为什么要进行 $LU$ 分解:
- 我们想要算出 $Ax = b$
- 我们用 $LU$ 替换 $A$,也就是 $A = LU$
- 那么就有 $(LU)x = b, L(Ux) = b$
- 令 $Ux = z$,因此有 $L(z) = b$
- 通过 $L(z) = b$ 算出 $z$
- 通过 $Ux = z$ 算出 $x$
- 因为是三角矩阵相关运算,因此比直接算容易很多
LU分解的 forward substitution:Lz = b
这一个分解是解出 $z$ 是多少,并提供给后面的 $Ux = z$。
回想一下之前高斯变换的 forward substitution,我们用一个代表消元的矩阵乘以
按照老办法,我们将 $L$ 也按四象分割。再自上往下分割 向量 $z$ 与 目标向量 $b$。根据 $Lz = b$ 我们可以得到以下等式:
$$
\left( \begin{array}{c | c}
1 & 0 \\
\hline
l_{21} & L_{22} \\
\end{array}
\right)
\left( \begin{array} {r}
\zeta_1 \\
\hline
z_2
\end{array}
\right)
=
\left(\begin{array}{r} \beta_1 \\ \hline b_2 \end{array}\right)
$$
化简后:
$$
\left( \begin{array} {c}
\zeta_1 \\
\hline
l_{21}\zeta_1 + L_{22}z{2}
\end{array}
\right)
=
\left(\begin{array}{c} \beta_1 \\ \hline b_2 \end{array}\right)
$$
因此可以得到关系:
- $\zeta_1 = \beta_1$
- $L_{22} z_2 = b_2 - \zeta_1 l_{21}$
注意 $L_{22}z_{2}$,是一个下三角单元矩阵与向量的乘积。这里与 $LU$ 分解类似,该乘积代表了更新后 $b$ 的值。而对其更新的是 $-l_{21}\zeta_1$。因此每次迭代中的更新的内容如下:
b2 = b2 -beta1 * l21b2 就是更新过的 $b$,也就是 $L_{22}z_{2}$。下面是整个算法:
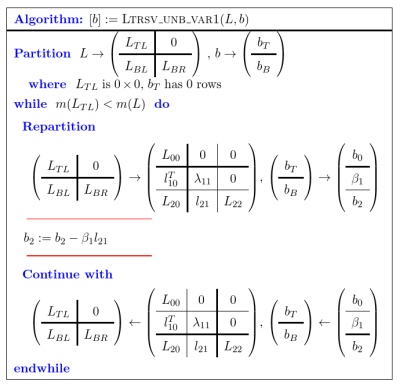
LU分解的 back substitution:Ux = z
之前解决了 $Lz = b$ 这个方程组,我们得到了现在我们需要求解 $Ux = z$ 。这一步是在求解 $x$ 是多少。按照之前的手法,将参与运算的单位都进行对应的分解,然后根据 $Ux = z$ 列出等式,有:
$$
\left( \begin{array}{c | c}
\nu_{11} & u_{12}^T \\
\hline
0 & U_{22} \\
\end{array}
\right)
\left( \begin{array} {r}
\chi_1 \\
\hline
x_2
\end{array}
\right)
=
\left(\begin{array}{r} \zeta_1 \\ \hline z_2 \end{array}\right)
$$
化简以后有:
$$
\left( \begin{array} {c}
\nu_{11}\chi_1 + u_{12}^Tx_2\\
\hline
U_{22}x_{2}
\end{array}
\right)
=
\left(\begin{array}{c} \zeta_1 \\ \hline z_2 \end{array}\right)
$$
这里跟之前有一些不同。想象一下之前高斯消元中的 back substitution,求解的过程是自下而上的。也就是说,我们会先解出 $x_2$,再代入 $x_2$ 解出 $x_1$,以此类推。那么我们再来看看上面的式子,其中第二行的关系是:
$$
U_{22}x_2 = z_2
$$
假设当前的循环开始于这么一个状态:
- 通过上一轮的的循环我们解出了 $x_2$ 部分
- 其他的运算还没有发生
那么作为结果的 $z$ 向量中,对应 $x_2$ 部分的分量 $z_2$,存放的就是上一轮计算出来的 $x_2$。因为此时并没有通过 $U_{22}x_2$ 来更新 $z_2$ 中的内容。因为 $z_2$ 是已知的,那么可以确定的是:
$$z_2 = x_2$$
再将这个结果带入到
$$\nu_{11}\chi_1 + u_{12}^Tx_2 = \zeta_1$$
可以得到:
$$ \chi_1 = (\zeta_1 - u_{12}^Tz_2) / \nu_{11} $$
那么可以看出来,整个循环的过程是这样的:
- 通过上一轮中得到的 $x_2$,我们更新了当前的 $\zeta_1$ 的内容
- 接着再用 $\zeta_1$ 的内容与 $\nu_{11}$ 相除,我们得到了新的 $chi_{1}$
接下来就是算法部分了。我们注意到,在逐步求出 $x$ 的过程中,每一次迭代中我们只会使用对应大小的 $z$ 的分量来求 $x$。这就意味着之前使用的 $z$ 中对应分量不会再使用到了,一个例子就是我们之前所提到的 $x_2 = z_2$。因此我们可以利用 $z$ 的空间来存储 $x$,也就是将每次求出的 $x$ 直接存储到 $z$ 中。那么循环部分的算法实际上就可以写成:
zeta1 = zeta1 - u12t * zeta2 // x1 = zeta1 -u12t *zeta2, zeta1 = x1;
zeta1 = zeta1 / u11 // update chi1
LU分解算法的消耗
- $LU$ 分解的消耗:$(2/3)n^3$
- 计算 $Lz=b$:$n^2$
- 计算 $Ux=z$:$n^2$
参考资料
- 本章所有非 svg 图片来源于 LAFF 课件