MITx: 18.01.2x Calculus 1B notes

来思考这么一个问题：我们在驾驶的过程中，如果知道了驾驶的平均速度，那么是否在驾驶的过程中，有那么一刻平均速度与该时刻的瞬时速度是相等的呢？

这个问题很容易转化为数学问题。由于平均速度在数学上可以用 Average Rate of Change，也就是几何上的 Secant Line 的斜率来表示；而瞬时速度则可以用 Instantaneous Rate of Change，也就是几何上某一点的 Tangent Line 的斜率来表示。因此，上述的问题实际就是在问：某个函数图像在指定的定义域之间，是否存在一点，使得该点的斜率与定义域首尾两点之间的连线的斜率平行？


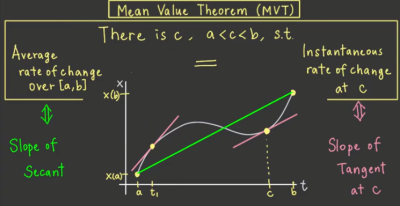
该问题的结论被称为中值定理（Mean Value Theorem），定义如下：

If is continuous on $a\leq t \leq b$, and differentiable on $a< t < b$, that is, $x'(t)$ is defined for all $a< t < b$, , then
$$\displaystyle \frac{x(b)-x(a)}{b-a} \, = x'(c) \qquad \text{for some }c,\, \, \text{with } a<c<b.$$

1.函数不连续的情况：



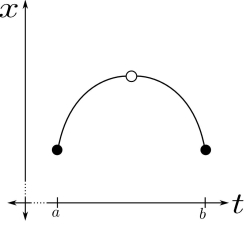
上图中拐点处的切线与起点和终点连线平行；但由于函数不连续，该拐点不存在；因此切线也不存在，MVT 在这种情况下失效。

2.函数不可微的情况



上图中拐点处因为是一个 Cusp，在该点函数无法微分，因此切线不存在；从而我们也无法找到与起点终点连线平行的切线，MVT 在该情况下也失效。

有些情况下，函数本身并不满足中值定理的前提，但结果却和中值定理的结论是一样的，比如下图：



该函数并不满足前提，但显然可以找到一点与函数的起点终点连线平行。

根据先前的问题，我们可以考虑一种特殊的情况：假设函数在区间 $[a,b]$ 上的起始点值相等，即 $f(a) = f(b)$。因此，$a、b$ 之间的连线一定与 $x$ 轴平行；也就是说，Secant Line 的斜率为 $0$。那么有没有可能在 $[a,b]$ 之间找到一点的切线与该连线平行（斜率为 $0$）？

根据导数的几何意义，切线斜率为 $0$ 的地方往往出现在拐点（极值点）。假设 $f(x)$ 在 $[a,b]$ 上连续，且在$(a,b)$ 上处处可微分；根据极值定理，我们可以判断 $f(x)$ 在 $[a,b]$ 上必定拥有最大值和最小值。 根据 $f(a)、f(b)$ 的值，上面的问题可以分成两种情况讨论：

1. 最大值等于最小值：因为 $f(a) = f(b)$，那么很显然该函数在 $[a,b]$ 上的图像是一条平行于 $x$ 的直线；也就是说 $f'(x)$ 必然为 $0$, 该函数上任意一点的切线均与点 $a、b$ 连线平行。
2. 最大值不等于最小值：因为 $f(a) = f(b)$，因此 $a、b$ 两点不可能同时作为最大值和最小值。综合极值定理可以推断，在 $(a,b)$ 之间必定存在一点 $c$，使得 $f(c)$ 为 $f(x)$ 在 $[a,b]$ 的最大值或者最小值。而我们知道最值出现的地方必定是函数图像的拐点，斜率必然为 $0$。由此可见这种情况也是成立的。

综上我们可以推断在特殊情况 $f(a) = f(b)$ 的时候，我们必然可以在区间 $[a,b]$ 上找到一点，其切线与 $a、b$ 的连线平行。用公式的形式可以表示如下：

Suppose a function $f(t)$ is continuous on $[a,b]$, and differentiable on $(a,b)$.there is must a point $c$,with $a<c<b$, such that:
$$\displaystyle f'(c)\, =\, 0 \, =\, \frac{0}{b-a} \, =\, \frac{f(b)-f(a)}{b-a}\qquad \textrm{since}\, f(a)=f(b).$$

上述定理被称为罗尔中值定理（Rolle's Theorem），是中值定理中的一种特殊形式。

罗尔中值定理有一个特殊的前提：起点与终点的值相等。那么当起点与终点的值不相等的时候，一个满足中值定理前提的函数，是否也有类似的性质呢？来看看下图：



该图描述了在上述的情况下中值定理的几何意义；其唯一的差别是 end points 的值不相等。因此，通过构造 end points 相等，我们就可以利用罗尔中值定理来证明上述的判定。

要使起点终点函数值相等，我们已使用当前函数减去 endpoints 的连线函数（second line）来达到函数在 endpoints 处相等的效果。具体的来讲：

令原函数为 $x(t)$，且该函数在 $[a,b]$ 上连续，且在 $(a,b)$ 上可微。那么原函数的起点为 $(a,x(a))$，终点为 $(b, (x(b))$。通过上述信息可知，该两点的连线的函数过点 $(a,x(a))$，且斜率为$\displaystyle \frac{x(b)-x(a)}{b-a}$。那么 $a,b$ 的连线函数可以表示为：

$$ g(t) = x(a)+ \frac{x(b)-x(a)}{b-a}(t-a) $$ 根据以上内容，我们构建的函数为：

$$ x_0(t) = \displaystyle x(t) - \left(x(a)+ \frac{x(b)-x(a)}{b-a}(t-a)\right) $$

由之前的推断可知，该函数适用罗尔定理。根据定理，$x_0(t)$ 在 $(a,b)$ 上必有一点 $c$，使得 $x_0'(c) = 0$。将上面的函数变形一下：

$$ x(t) = \displaystyle x_0(t) - \left(x(a)+ \frac{x(b)-x(a)}{b-a}(t-a)\right) $$

对 $x(t)$ 左右两边同时求导，可得：

$$ x'(t) = x_0'(t) + \frac{x(b)-x(a)}{b-a} $$

令 $t = c$，上面的式子可以写成：

$$ x'(c) = x_0'(c) + \frac{x(b)-x(a)}{b-a} $$

因为 $x_0'(c) = 0$，因此该式可以写成：

$$ x'(c) = 0 + \frac{x(b)-x(a)}{b-a} = \frac{x(b)-x(a)}{b-a} $$

我们发现，$x(t) $在 $c$ 点处的切线斜率，与$x(t)$ 上 $a、b$ 两点连线的斜率是相等的。因此，我们可以得出以下结论：

If $x(t)$ is continuous on $a≤t≤b$, and differentiable on $a<t<$b, that is, $x′(t)$ is defined for all $t$, $a<t<b$, then

$$\displaystyle \frac{x(b)-x(a)}{b-a} \, = x'(c) \qquad \text {for some }c,\, \, \text {with } a<c<b.$$

该定理被命名为拉格朗日中值定理（Lagrange Mean Value Theorem），该定理是罗尔中值定理的推广形式。

导数可以用于判断函数的走势；该性质大致可以总结如下：

If $x′(t)≥0$ for all $t$ in $(A,B)$, then $x(t)$ is increasing or staying the same over $[A,B]$.
If $x′(t)≤0$ for all $t$ in $(A,B)$, then $x(t)$ is decreasing or staying the same over $[A,B]$.
If $x′(t)=0$ for all $t$ in $(A,B)$, then $x(t)$ is constant over $[A,B]$.
If $x′(t)>0$ for all $t$ in $(A,B)$, then $x(t)$ is strictly increasing over $[A,B]$.
If $x′(t)<0$ for all $t$ in $(A,B)$, then $x(t)$ is strictly decreasing over $[A,B]$.

上述的总结我们可以用中值定理来对其进行证明。

为了使用中值定理证明上述的性质，我们需要引进两个概念：上界（Upper bound）和下界（Lower bound）。我们使用 $M$ 表示上界， $m$ 表示下界；这两个概念的定义如下：

A number $M$ is an upper bound on a function $f(x)$ if $f(x) \geq M$ for all $x$
A number $m$ is an lower bound on a function $f(x)$ if $f(x) \leq m$ for all $x$

而这两个标记也可以用于指定的区间上，他们与函数的关系可以记做：

$$ m \leq f(x) \leq M \,\,\displaystyle \text {for all } \, \, x\, \, \text {in}\, \, [a,b] $$

一个函数可能拥有数个上界和下界，那么上界中最小的一个，我们称之为最小上界（least upper bound），而下界中最大的一个，我们称之为最大下界（ greatest lower bound）。这两者都被称为 best upper & lower bound。很明显，“Best” 这个词是在描述离函数最近的属性。

如何证明下面的导数性质？

if the derivative of a function is non-negative, then the function is increasing or staying at the same value.

假设函数 $x(t)$ 满足 MVT： 在 $[A,B]$ 上连续，并且在 $(A,B)$ 上可微。可知 $x'(t)$ 的表达式为：
$$ x'(t) = \frac{x(B)-x(A)}{B-A} $$ 假设 $m$ 为 $x'(t)$ 的下界，那么根据中值定理，则有：

$$ m \leq \frac{x(B)-x(A)}{B-A}, \,\, \text{for all t such as A < t < B} $$
现在我们假设有一个区间 $[a,b]$ 处于 $(A,B)$ 之间，即 $A \leq a < b \leq B$。由 MVT 在区间 $(A,B)$ 上适用，可知在区间 $(a,b)$ 上适用。因此，$x(t)$ 在 $(A,B)$ 上的 lower bound 也适用于 $[a,b]$：
$$ \displaystyle \displaystyle m\leq \frac{x(b)-x(a)}{b-a} \, \, \text { for ALL }\, a,b\, \text {such that} \, \, A\leq a<b\leq B. $$
现在令 lower bound $m = 0$，因为 $b > a$，因此 $x(b) \geq x(a)$。

因此，对于函数 $x(t)$，上述的不等式说明了函数 $x(t)$ 在 $[A,B]$ 上的趋势是递增或者是保持不变（当 $x(a) = x(b)$ 时）。这与我们之前学习的导数性质是符合的。

同理，令 $x'(t) \leq 0$（即 $0$ 为 $x'(t)$ 的上界），也可以证明导数为负时函数的趋势为下降的性质。

“ The subtlety is that the MVT relates the infinitesimal behavior of the function, the derivative, which is defined at each point, with the macroscopic behavior, the total change over an interval.”

问题：已知函数 $\displaystyle f(x) = -\frac{x^3}{6} - 3x - 2 \cos x$，如何判断该函数的根有多少个？

• 首先从函数自身判断：当 $x \to -\infty$ 时，$f(x) \to \infty$；当 $x \to +\infty$ 时，$f(x) \to -\infty$。根据 IVT 可知，函数图像必定穿过 $x$ 轴，因此，该函数至少有一个根。
• 其次，该函数的导数 $\displaystyle \displaystyle f'(x) = -\frac{x^2}{2} - 3 + 2 \sin x$。该导数在整个 $x$ 的定义域上都是恒为负的，也就是 $f'(x) < 0$， $f(x)$ 在定义域上单调递减，$f(x)$ 的图像只能穿过 $x$ 轴一次。因此，该函数有且只有一个根。

如果是比较两个函数的大小，该类的问题实际上可以转换成讨论另外一个函数的正负问题。即比较$f(x)$ 与 $g(x)$ 的大小，我们可以令 $h(x) = f(x) - g(x)$，通过讨论 $h(x)$ 的正负来反映 $f(x)、g(x)$ 的关系。而 $h(x)$ 本身拥有表达式；因此我们可以利用其导数的性质来作出判断。

例A：证明 $\displaystyle e^ x>1+x \text { for all } x>0$。

由题，令 $h(x) = e^x - (1+x)$。

• 首先判断是否存在 $x$ 使得 $h(x) = 0$。本例中，令 $e^x - (1+x) = 0$， 则可算出当 $x =0 $ 时 $h(x) = 0$。
• 接下来判断 $h'(x)$ 的正负。 显而易见的是，$h'(x)=e^ x-1 \, >0$ 对于所有的 $x > 0$ 都成立。根据导数性质，可知 $h(x)$ 在 所有的 $x>0$ 上单调递增的。因为 $h(0) = 0$，因此 $h(x)$ 在$(x , +\infty)$ 上是恒大于 $0$ 的，即 $e^ x>1+x \,\, \text{for all} \,\, x>0$，问题得证。

级数的示例

由 MVT 可知， average rate of change 与区间$[a,b]$上某一点的导数相等。当该导函数存在 bounding 时，很容易得出： $$ \displaystyle \text{for all}\, \, c\, \, \text{with}\, \, a<c<b, $$ 很显然，导函数 $x'(t)$ 的上下界也是 average rate of change 的上下界： $$ m \leq \displaystyle \frac{x(b)-x(a)}{b-a} \leq M \,\,\,\displaystyle \text {(Bounds on the average rate of change).} $$ 由于 $b - a >0$，因此上述不等式可以改写为： $$ \displaystyle m \cdot (b-a) \leq x(b) -x(a) \leq M \cdot(b-a) \text{(Bounds on the total change)} $$ 也就是说，函数 $x'(t)$在区间 $[a,b]$ 上的变化量也是有一个上下限的，值如上面的不等式所示。 根据极值定理，连续的函数在某个闭区间上必定有最大值和最小值。对于函数来说，其自身的最大值和最小值即是该函数的最小上界和最大下界。因此，先前的关系可以转写为：

$$ \displaystyle m \leq \displaystyle \displaystyle \min _{a \leq t \leq b} x'(t) \displaystyle \leq \displaystyle \frac{x(b)-x(a)}{b-a} \displaystyle \leq\displaystyle \max _{a\leq t \leq b} x'(t) \leq \displaystyle M $$

例B：下列不等式是否成立?
$$ \displaystyle \tan (\theta )-\tan (\phi )\, \geq \, \theta -\phi \qquad \left(\text {for all }\, \, -\frac{\pi }{2}<\phi <\theta <\frac{\pi }{2}\right) $$ 将上述不等式变形，可以看出来是函数 $tan$ 的导数形式：

$$ \displaystyle \frac{\tan (\theta )-\tan (\phi )}{\theta -\phi } = tan'(\theta) $$ 因为 $\theta >\phi$，根据 MVT，有：
$$ \displaystyle \frac{\tan (\theta )-\tan (\phi )}{\theta -\phi }\, \geq \, \min _{-\frac{\pi }{2}<\theta <\frac{\pi }{2}} \tan '(\theta )\qquad \text {for any } -\frac{\pi }{2}<\phi <\theta <\frac{\pi }{2}. $$ 对其导数进行计算，有：
$$ \displaystyle \frac{d}{d\theta } \tan (\theta ) = \, \sec ^2(\theta )\, \geq 1 \qquad \text { for all } -\frac{\pi }{2}<\theta <\frac{\pi }{2}. $$ 因此可知， $$ \displaystyle \frac{\tan (\theta )-\tan (\phi )}{\theta -\phi }\geq 1 \qquad \text { for all } -\frac{\pi }{2}<\phi <\theta <\frac{\pi }{2} $$ 变形一下，则可知题目命题成立。

MVT 和 线性近似都可以用于表达函数的平均变化率($\frac{\delta x}{\delta t}$)。这两者的区别在于：

• 线性近似能找到函数上一个确定的点，通过该点的斜率来计算另外一个点处函数的值，但这个值是近似的（$\Delta x \approx x'(a)\cdot \Delta t $）。
• MVT只知道函数上的某一点导数然等于平均变化率，我们不能确定该点的位置，但计算出来的平均变化率是绝对准确的（$\Delta x = x'(c)\cdot \Delta t$）。

$$\Delta x \approx x'(a) \Delta t$$



$$\Delta x = x'(c) \Delta t$$

以上两图来源：EDX MIT 6.001 课程插图。

为了更好的理解接下来的知识，我们采用了莱布尼兹的写法来对微分做正式的标记：

Let $y=F(x)$, the differential of y is defined as：

$$\displaystyle dy \, = \, F'(x) dx$$
This is also called the differential of F and denoted $dF$.

这个标记来自于莱布尼兹对导数的标记：
$$ \displaystyle F'(x)= \frac{dy}{dx} \qquad \left(\text {or} \, \, \frac{ dF}{dx}\right) $$
莱布尼兹标记将 $dx$ 视作与无穷小的比率（ratio of infinitesimal）换句话说，我们可以将导数理解为微分 $dy$ 与 $dx$ 的比率。

我们可以将线性近似与微分做一个比较，两者最大的差异在精度上（也就是 $\Delta x$ 是离散的细分，而 $dx$ 是无穷小级别的细分）：


即：

• 线性近似：$\Delta F \approx F'(x) \, \Delta x, \Delta x\text{ is a finite change in x}$
• 微分：$dF = F'(x)dx \, \text{, dx is tiny bit of x}$

• 两个函数和的微分公式：$\displaystyle d (F+G) = \displaystyle dF+dG$
• 与常数乘积的微分公式：$\displaystyle d(k\cdot F) = \displaystyle k \, dF$
• 两个函数乘积的微分公式：$\displaystyle d(F\cdot G) = \displaystyle \left(F' \cdot G+ F\cdot G'\right) \, dx= G(dF) +F(dG)$

线性近似使用某一点 $x_0$ 处切线的斜率（导数）加上该点的坐标求出一个线性函数，用该线性函数来模拟得到另外一点在原函数上的值。

通常情况下，线性近似模拟出的在 $y$ 上的变化率 $\Delta y$ 可以用以下公式计算：

$$ f(x+\Delta x) \approx y + \Delta y $$ 由于微分可以代替线性近似中 $x$ 的变化率 $\Delta x$，因此使用微分的线性近似可以写成下面的形式：

$$ f(x + dx) \approx y + dy $$

例A：现有函数 $f(x) = \sqrt{10x - x^2}$，其中 $f(2) = 4, f(3) = \sqrt{21}$。使用微分在 $x_0 = 2$处进行线性近似，估算 $\sqrt{21}$ 的值。

本题需要求 $f(3)$ 的值，因为已知 $f(2)$ 的值，很容易想象到的是 $f(3) = f(2+1)$。按照之前的公式：$f(x + dx) = y + dy$，可以得知此处：

1. $dx = 1$
2. $x = 2$
3. $y = 4$

那么整个公式就可以写成：
$$ f(2 + 1) = 4 + dy $$

因此，我们只需要求得 $x=2$ 时，按照线性近似计算出的变化率 $dy$ 即可。根据微分公式，则有：

$$ dy = \left.\displaystyle \frac{dy}{dx}\right|_{x=2} dx $$
直接对 $f(x)$ 求导，再将$x=2$ 计算出的导数，这样即可得到 $dy$ 的值。最后将 $dy$ 的值与原函数在 $x=2$ 处的值相加，即可得到结果（具体过程略）。

注：这里不定积分指 Anti-derivatives，正式用法是 Indefinite integral，中文未做区分。

先来看看不定积分的定义：

An antiderivative (Indefinite integral) of $f(x)$ is any function $F(x)$ such that
$$\displaystyle F'(x)\, = f(x).$$

为什么会称之为不定积分？

举一个例子：$\displaystyle \int sin(x) dx = ?$
很容易想到的一个答案是 $\displaystyle \int sin(x) dx = -cos(x)$，因为 $-cos(x)$ 的导数是 $sin(x)$。但由于常数项在求导以后会变为 $0$，假设 $C$ 为常数，很显然 $-cos(x) + C$ 的导数也是 $sin(x)$。这就意味着，$\displaystyle \int sin(x) dx$ 不但可以为 $-cos(x)$，也可以是 $-cos(x)$ 加上任意常数 $C$。这意味着该积分的结果实际上是一系列满足条件函数的集合。基于这种性质，我们称这样的积分为不定积分。正式的定义如下：

Given a function $f(x)$, the indefinite integral or the antiderivative of $f(x)$ is denoted $\displaystyle \int f(x)dx$. It is the family of functions:
$$\displaystyle \int f(x) \, dx \, = F(x) + C$$
where $F(x)$ is any antiderivative of $f(x)$, that is, $F'(x)=f(x)$, and $C$ is any constant.

我们称 $\displaystyle \int$ 为积分符号(integral sign), $f(x)$ 为被积函数 (integrand), and $C$ 为积分常数(constant of integration)。

根据 Power Rule 可知，一般幂函数微分的形式可以写作：
$$d(x^{a+1}) = (a+1)x^adx \,\,\, \text{(2.4.1)}$$ 对该形式变形：
$$ x^adx = \frac {d(x^{a+1})}{a+1} $$
对两边同时取积分，我们可以推出对幂函数积分的一般公式：
$$ \int x^adx = \frac{x^{a+1}}{a+1} +C \,\,\,\text{(2.4.2)} $$
不过这里有一个问题。对比结论 $2.4.1$ 与 $2.4.2$ 发现，在 $2.4.2$ 中， $a+1$ 做了分母，因此 $a$ 不能等于 $-1$。因此，需要对 $a=-1$ 的情况单独讨论。

我们将 $a=1$ 的情况直接带入 $2.4.2$ 的左边部分，结果有了新的发现：
$$ \int x^adx = \int \frac{dx}{x} $$
这个被积函数非常明显，一看就是 $lnx$ 的导数。根据对数的求导公式，我们可以计算该积分为：
$$ \int \frac{dx}{x} = lnx + C $$
不过这里还有一个问题。我们知道 $lnx$ 只有在大于 $x>0$ 的时候才有意义。当 $x < 0$ 时情况下，我们需要验证该积分是否也会得到 $ln(x)$ 的结果。由 $x<0$，可知 $-x>0$，那么只要 $ln(-x)$ 的微分结果也是 $\frac{1}{x}$，我们就可以得出更加通用的结论：

\[ \begin{align*} \frac{d}{dx}ln|x| &= \frac{d}{dx}ln(-x) \\\\ &= \frac{1}{-x} \cdot \frac{d}{dx}(-x) \\\\ &= \frac{1}{x} \end{align*} \]

我们发现对于 $|x|$，无论 $x$ 的正负，其导数的值都是 $\frac{1}{x}$，因此，在 $a=-1$ 的情况下，幂函数函数的公式可以总结为：

$$ \int \frac{dx}{x} = \ln \left(|x|\right)+C $$
综上， 幂函数的不定积分公式可以归纳为：

$$ \displaystyle \int \, x^ p\ dx \, \, = \qquad \begin{cases} \displaystyle \frac{x^{p+1}}{p+1} +C & \mbox{if } p \neq -1 \\ \ln \left(|x|\right)+C & \mbox{if } p = -1. \end{cases} $$

积分作为微分的逆运算，是需要通过 MVT 来保证结果的（常数 $C$）；如果我们希望对某个函数求积分，那么该函数的原函数必须在指定的区间上连续而且处处可微。如果某处不连续，那么我们必须严格的按照分段来讨论。否则，我们无法保证求出来的表达式是否正确。

举例说明，假设我们有分段函数如下： $$ \left\{\begin{matrix} g(x)=\frac{1}{x} \,\,\,\text{x>0} \\ g(x)=\frac{1}{x}+2 \,\,\, \text{ x<0} \end{matrix}\right. $$ 对两个函数进行分别计算，其导数都为 $-\frac{1}{x^2}$。但如果简单的以该导数作为基础来求这个分段函数的积分的话，我们会得到： $$ \int -\frac{1}{x^2}dx=\frac{1}{x}+C $$ 而我们发现通过这个公式，我们是无法通过平移来得到之前分段函数的图像的。从图像上来说，$1/x$ 是基于原点对称的，而我们的分段函数是基于 $y$ 轴对称的。

因此，对于公式中的 $\int \frac{1}{x} dx=\ln \left(|x|\right)+C$，也必须按照 $x$ 的正负来分别进行积分的计算，也就是下面的形式：

$$ \left\{\begin{matrix} ln(x)+C \,\,\,\text{x>0} \\ ln(-x)+C \,\,\, \text{ x<0} \end{matrix}\right. $$

根据求导的公式我们可以总结一些不定积分的公式如下：

• $\displaystyle \int e^ x \, dx=e^ x+C$
• $\displaystyle \int \cos (x) \, dx=\sin (x)+C$
• $\displaystyle \int \frac{1}{1+x^2} \, dx=\arctan (x)+C$
• $\displaystyle \int \frac{1}{\sqrt {1-x^2}} \, dx=\arcsin (x)+C$
• $\displaystyle \int \sec (x)\tan (x) \, dx=\sec (x)+C$
• $\displaystyle \int tan(x) dx = ln|sec(x)| + C$

该性质如下：

$$ \displaystyle \int k \, f(x)\, dx= k \int \, f(x) \, dx $$

简易证明：令 $F' = f$，那么 $(kF') = kF' = kf$ ，因此可得：
$$ \displaystyle \displaystyle \int k \, f(x) \, dx\ =\ k F(x)+C $$
根据上式，我们有：
$$\displaystyle \displaystyle k \ \left(\int \, f(x)\, dx\right) \ =\ k \cdot (F(x)+C) = k F(x) +k\cdot C \ =\ k F(x) + C_1$$
可以看出 $\displaystyle \int k \, f(x)\, dx$ 与 $ \displaystyle k \ \left(\int \, f(x)\, dx\right)$ 的结果差异仅在一个常数上。他们表现的是拥有相同导数的一组函数中的某一员，对于不定积分来说，两者是等价的。

该性质表现为如下公式：

$$ \displaystyle \int \left(f(x)+g(x)\right)\, dx= \int f(x) \, dx + \int g(x) \, dx $$

简易证明：

令 $F' = f, G' = g$，那么 $(F+G)' = F' +G' = f+g$。

根据上述结果，我们有：

$$ \displaystyle \int \left(f(x)+g(x)\right) \, \, dx\ =\ F(x)+G(x) +C $$

又因为：
\begin{align} \displaystyle \displaystyle \int f(x)\, dx +\int g(x) \, dx &= \displaystyle \ (F(x)+C_1) +(G(x) +C_2)\\\\ &= \displaystyle F(x)+G(x)+(C_1+C_2) \end{align} 前面提到，在不定积分中，可以认为只有常数不同的函数是等价的；因此之前的性质成立。

该性质表现为如下：

$$\displaystyle \displaystyle \int f\cdot g\, \, dx \,\, \displaystyle \textbf{DOES NOT EQUAL} \,\, \displaystyle \ \left( \int \, f \, dx\right)\cdot \left(\int \, g \, dx\right)$$
$$\displaystyle \int \frac{f}{g} \, dx \,\, \displaystyle \textbf{DOES NOT EQUAL} \,\, \displaystyle \frac{ \int f \, dx }{ \int g\, dx}$$

以上的性质均可通过导数的性质进行验证。

首先来看一个例子：

$$\int 3(sin(x))^2cos(x)dx$$

这样的乘积形式并不是我们之前遇到的基本形式，也不能应用第一准则。但我们可以发现的是，$cos(x)$ 正好是 $sin(x)$ 的导数。于是我们令 $u =sin(x)$，那么实际上这个积分就可以转换为：

$$\int 3u^2u' dx$$

接下来我们对 $u$ 进行 $x$ 的微分，那么有：$du = cos(x)dx = u'dx$。那么式子就可以转化为：

$$\int 3u^2 \cdot du$$

于是我们根据基本的幂函数积分公式就可以求得上述的积分结果，再将 $u =sin(x)$ 代入该积分结果即可得到最终结果。


上面的方法在遇到某些乘积形式的积分时（实际上是 Chain Rule 微分的一种表现形式）非常有用；我们将这种通过替换部分函数简化运算的方法称为换元法（Method of substitution）。来看一看正式的定义：

The method of substitution is the integration analogue of the chain rule, If:
$$g(x)dx = \displaystyle f(u(x)) \, u'(x) dx,$$
that is, the integrand $g(x)$ can be seen as the result of a chain rule, then:
\begin{align} \displaystyle \displaystyle \int g(x)\, dx &= \displaystyle \int f(u(x))\, u'(x)\, dx\\\\ &=\displaystyle \int f(u)\, du\\\\ &=\displaystyle F(u(x))+C \end{align}

假设我们有如下不定积分:
$$y=\int f(x)dx$$

上述积分的结果是导数为 $f(x)$ 的所有函数的集合。因此我们可以得到以下的关系：
$$\frac{dy}{dx} = f(x)$$

我们称这个形式的等式为微分方程（Differential Equations）。

为什么要去解这类方程呢？

来看一个物理学中的例子：$F=ma$。我们知道，$a$ 是物体的加速度，也就是距离之于时间的二阶导数。如果将距离表示为 $x$，那么上述的方程可以写为：

$$F=m \frac{dv}{dt} = m \frac{d^2x}{dt^2}$$

如果我们想知道 $F$ 与 $m$ 之间的关系如何，那么我们可以通过 $t$ 和 $x$ 的关系来解如下的微分方程：
$$ F/m = \frac{d^2x}{dt^2} $$
因此，如果我们想求的不是具体的数，而是描述关系的函数，那么就需要建立微分方程并求解。

为了计算过程中的方便，数学上往往将微分的过程记做：$\displaystyle \frac{d}{dx},\, or \,D_x$。该形式可以看做是一个运算符，我们称为微分算子（Differential operator）。微分算子代表了一个运算过程：接受一个函数，得到另外一个函数。对于微分算子，有以下等价的关系：

$$ \frac{d}{dx}(f(x)) = \frac{df}{dx} = f'(x) $$

有一些微分方程的形式是可分解（Separable）的，比如如下的方程：
$$ \frac{dy}{dx} = xy $$
这样的微分方程乍一看有两个变量，不是很好求解。但实际上，这样的方程可以分解为如下形式：

$$ \frac{dy}{y} = dx\cdot x $$
我们对方程两边分别求积分：
$$ \int \frac{dy}{y} = \int xdx $$
通过上面的步骤就可以得到 $y$ 的最终表达式，也就是本例微分方程的解了。

前面提到微分方程的解是一系列满足条件的函数。如果我们需要指定其中的某一个函数，我们可以通过指定对应的变量值来确定这个函数。这一组对应的变量值，被称为初始条件（Initial Conditions）。通过将这一组变量值代入微分方程的通用解，我们可以求出常数 $C$ 在该特定条件下的值，从而得出该特定函数的表达式。比如如下例子：

$\displaystyle \ \frac{dy}{dx} = y$ 的通用解是 $\displaystyle y = Ce^x$，如果我们已知初始条件 $y(0) = -2$ （即函数过点 $(0,-2)$），那么将这一组值代入通用解表达式计算可得出 $C$ 的值，从而可以得出该微分方程过 $(0,-2)$ 的独特解为 $y=-2e^x$。

然而，并不是所有的初始条件都可以得到微分方程的独特解。对于这种情况，有一个定理如下：

Given a differential equation $\displaystyle \frac{dy}{dx}=f(x)g(y)$ and an initial condition $y(a)=b$, if $f, g$, and $g′$ are continuous near $(a,b)$, then there is a unique function $y$ whose derivative is given by $f(x)g(y)$ and that passes through the point $(a,b)$.

可以看出来，确保有独特解必须要两个条件：

• 微分方程可分解 （$f(x)g(y)$ 形式）
• 方程内所有函数必须连续。
• 被微函数的导数必须连续。

有一些微分方程是不能被分解的。对于此类方程，我们可以用近似的方法来获取他的图像。我们知道导数是用于描述函数运动趋势的，因此我们可以采样一些点（初值），来看看函数的大概的走势如何。

因为微分方程的左边都可以看作是函数在某点切线的斜率，根据微分方程，我们代入初始条件的值就可以直接得到函数在该点斜率的值。利用该性质，我们可以建立一个网格，将网格上的点作为初始条件带入到微分方程中，得到对应的斜率结果，并将该结果以斜率的方式画到图上，这样就能在图像上判断函数解的大致图像了。 来看一个例子：$\displaystyle \frac{dy}{dx} = x+y$，该函数的斜率图如下所示：



Slope field 作为一种近似的手段，通常用于求一些不可解的微分方程的近似值。该近似的过程实际上是一个迭代的过程，可以很轻松的使用电脑来完成计算。

有了上述的图，我们可以判断函数的大致的走势了。来想象一下要怎么描绘这个函数：

1. 因为我们有斜率图，因此我们可以最大程度的利用这些信息。
2. 假设函数从某一点 $x_0$ 出发：此时该点的斜率（微分方程），以及该点的位置（初始条件）是已知的
3. 设想该函数通过某一个点 $x_1$，而该点离 $x_0$ 够近。
4. 使用指定的近似方法来预测函数的下一个点在哪里。精度（$\Delta x$） 由我们自行指定。

以线性近似为例，根据以上条件，我们可以得到方程在 $x_1$ 点处的近似值：

$$ f(x_1) = f(x_0+ \Delta x) = \frac {dy}{dx_0} \cdot \Delta x + f(x_0) $$

获得上述信息后，$x_0$ 到 $x_1$ 之间的图像就确定了。接下来以当前的 $x_1$ 为新的起点，重复之前的步骤，找出 $x_1$ 下一个点 $x_2$ 之间的函数近似图像。通过这样反复的迭代，最终可以得到一条由线性近似的的线段组成的“曲线”：


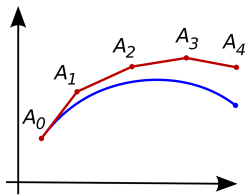
图片来源：WikiPedia

我们将上述描绘函数的方法称之为欧拉方法（Euler's Method）。

以$\displaystyle \frac{dy}{dx} = x+y$ 与线性近似的组合为例，来总结一下欧拉方法的步骤：

1. 确定 $\Delta x$，也就是精度的大小（此处记为 $h$ ）
2. 设定初始条件值，也就是函数的出发点 $(x_0, y_0)$
3. 根据线性近似我们可以算出下一个点的坐标，即：
   1. $x_1 = x_0+h$
   2. $y_1 = y_0+(x_0+y_0)h$
4. 很显然，我们可以得到上述步骤的迭代表达式：
   1. $x_{k+1} = x_k+h$
   2. $y_{k+1} = y_k+(x_k+y_k)h$

该方法的 python 版本如下：

#set initial condition
x,y = x0, y0
#set step size
h=0.1
#count iterations of method
stepcounter = 0
#determine how many steps to take
while stepcounter < 1000:
   y= y+(x+y)*h
   x+=h
   stepcounter+= 1

• 拉格朗日定理与罗尔定理，柯西定理啥关系?
• 关于拉格朗日中值定理的证明（解决MIT C1.S5如何处构造辅助函数 x0t 的问题）
• 积分表
• 用Python学《微积分B》（微分方程）
• Summary PDF：MVT | Differentials and antiderivatives